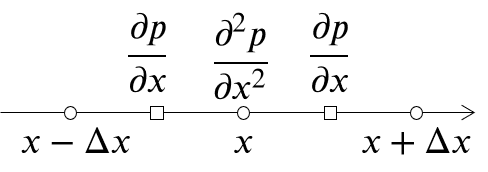背景
姫野ベンチマークは理化学研究所の姫野龍太郎博士が考案したベンチマークである.公式の解説では,
姫野ベンチマークは情報基盤センター・センター長の姫野龍太郎氏が非圧縮流体解析コードの性能評価のために考えたものでポアッソン方程式解法をヤコビの反復法で解く場合に主要なループの処理速度を計るものです。
と書かれているが,どのように非圧縮流体解析と関連があるかや,姫野ベンチマークの挙動自体の解説は見かけない.
モダンFortran勉強会の中から並列計算勉強会が立ち上がり,do concurrentの学習に際して姫野ベンチマークを題材にしようという声があったため,解説を作成した.
実装については,Fortran 90版のソースコードを引用している.
非圧縮性流体解析のアルゴリズム,あるいはPoisson方程式が現れる理由
基礎式
非圧縮性流体解析では,流れに非圧縮性を仮定し,連続の式(1)とNavier-Stokes方程式(2)を基礎式とする.(本稿では姫野ベンチマークの解説にあわせて,非圧縮性流体解析と表現する.)
\begin{align}
\nabla \cdot \boldsymbol{u} &= 0\qquad (1)\\
\frac{\partial \boldsymbol{u}}{\partial t} + \left( \boldsymbol{u}\cdot \nabla \right)\boldsymbol{u} &= -\frac{1}{\rho}\nabla p + \nu \nabla^2 \boldsymbol{u}\qquad (2)
\end{align}
ここで,$\boldsymbol{u}$は速度,$p$は圧力である.非圧縮性流体解析の目的は,ある流れの速度と圧力の時間変化を時々刻々計算し,得られた速度や圧力を注意深く確認し,有意な知見を見出すことである.このとき,基礎式では,速度の時間変化$\partial \boldsymbol{u}/\partial t$は式(2)に現れているが,圧力の時間変化$\partial p/\partial t$は現れない.そのため,圧力の時間変化を陽に追跡できず,速度の時間変化にあわせて式(1)を満たすような圧力の分布を,何らかの方法で求めなければならない.非圧縮性流体解析のアルゴリズムとは,この圧力をどのように計算するかの工夫であると言っても過言ではない.非圧縮性流体解析のアルゴリズムとして,MAC法や部分段階法を以下で説明する.
MAC法
MAC法はMarker and Cell法の略で,本来は自表面を持つ流れを計算する方法として提案されたのであるが,空間の離散化と時間発展のアイデアが優れていたので,広く使われた.現在は時間発展のアルゴリズムを指してMAC法とよばれている.
Mac法では,まず式(2)の発散をとり,$D \equiv \nabla\cdot\boldsymbol{u}$とおくと,$D$の時間変化に関する式が得られる.
\frac{\partial D}{\partial t} + \nabla\cdot\left\{\left( \boldsymbol{u}\cdot \nabla \right)\boldsymbol{u}\right\} = -\frac{1}{\rho}\nabla^2 p + \nu \nabla^2 D \qquad (3)
時間微分項を前進Euler法によって離散化する.上付き添字$n$は時刻を表しており,時間微分項以外の項は,全て時刻$n$の値を用いることにする.
\frac{D^{n+1} - D^n}{\Delta t} + \nabla\cdot\left\{\left( \boldsymbol{u}^n\cdot \nabla \right)\boldsymbol{u}^n\right\} = -\frac{1}{\rho}\nabla^2 p^n + \nu \nabla^2 D^n \qquad(4)
さて,次の時刻$n+1$において速度が連続の式を満たさなければならない.すなわち,$\nabla\cdot\boldsymbol{u}^{n+1}=D^{n+1}=0$である必要がある.
それには,式(4)において
\frac{D^n}{\Delta t} - \nabla\cdot\left\{\left( \boldsymbol{u}^n\cdot \nabla \right)\boldsymbol{u}^n\right\}-\frac{1}{\rho}\nabla^2 p^n + \nu \nabla^2 D^n=0 \qquad(5)
でなければならない.ここで,$D^n$は本来$0$になるはずであるが,様々な事情で$0$にならないことを考慮して残されている.速度が関係する項を右辺に,圧力を左辺に置くと,これは時刻$n$における速度と圧力の関係を表すPoisson方程式となる.
\nabla^2 p^n = \rho\left[\frac{D^n}{\Delta t} - \nabla\cdot\left\{\left( \boldsymbol{u}^n\cdot \nabla \right)\boldsymbol{u}^n\right\} + \nu \nabla^2 D^n\right] \qquad(6)
非圧縮性流体解析では,これを圧力Poisson方程式とよんでいる.単純にPoisson方程式とよぶこともある.空間を離散化して,空間微分を何らかの方法で離散的な処理に置き換えると,式(6)は圧力$p$に関する連立方程式となる.その連立方程式を解くことで,次の時刻において速度の発散を0にするような圧力$p^n$が得られる.
MAC法では,$\boldsymbol{u}^n$が既知の時,次のような手順で流れ場の時間発展を計算する.
- 式(6)を用いて$\boldsymbol{u}^n$から圧力$p^n$を計算する.
- Navier-Stokes方程式に$\boldsymbol{u}^n$と$p^n$を代入して次の時刻の速度を計算する.
\frac{\boldsymbol{u}^{n+1} - \boldsymbol{u}^n}{\Delta t} + \left( \boldsymbol{u}^n\cdot \nabla \right)\boldsymbol{u}^n = -\frac{1}{\rho}\nabla^2 p^n + \nu \nabla^2 \boldsymbol{u}^n \qquad(7)
MAC法の特長は,式(6)の中に$D^{n}$が残っていることである.$D^n$は本来$0$になっていなければならない.一方で,圧力に関する連立方程式を解くのに非常に長い時間がかかるので,連立方程式を真面目に解かず,近似的に解くことが行われている.そのような場合,$D^n$が$0$にならないのであるが,MAC法では$D^n$の項も式に残されているため,$D^n\neq 0$であることも考慮して$D^{n+1}$を$0$にするような式になっている.つまり,(幾分語弊はあるが)圧力に関する連立方程式を適当に解いても,その影響は次の時刻に影響を与えにくい.
また,式(6)を解いて得られた圧力$p^n$は,$\nabla p^n$として式(7)中で用いられるので,$\nabla^2 p^n = \nabla\cdot(\nabla p^n)$が離散的にも成立しなければならない.MAC法で導入されたスタガード格子はそれを可能にする.
これらの特長があるため,MAC法は現在の非圧縮性流体解析の主流解法の礎となった.残念ながら,MAC法の名前の由来となったMarker(自由表面流れの解法)を見かけることは,非常にまれである.
部分段階法(Fractional Step法)
MAC法とは別の方法として,よく使われる部分段階法も紹介する.
非圧縮性流体解析の難しさは,連続の式(1)を満たすような圧力を求めることにあった.部分段階法では,まず式(2)中の圧力勾配の項を無視して速度の時間発展を計算した後,圧力勾配の影響による速度の時間発展を計算する.ここで使う圧力は,次の時刻の圧力である.
まず,式(2)の時間微分項を前進Euler法によって離散化する.圧力は時刻$n+1$の値を,速度は時刻$n$の値を用いると,次式が得られる.
\frac{\boldsymbol{u}^{n+1} - \boldsymbol{u}^n}{\Delta t} + \left\{\left( \boldsymbol{u}^n\cdot \nabla \right)\boldsymbol{u}^n\right\} = -\frac{1}{\rho}\nabla p^{n+1} + \nu \nabla^2 \boldsymbol{u}^n \qquad(9)
ここで,$p^{n+1}$は直ちには判らないので,圧力を無視して式(9)を計算する.
\frac{\boldsymbol{u}^{*} - \boldsymbol{u}^n}{\Delta t} + \left\{\left( \boldsymbol{u}^n\cdot \nabla \right)\boldsymbol{u}^n\right\} = \nu \nabla^2 \boldsymbol{u}^n \qquad(10)
圧力の影響を無視しているので,得られる速度は$\boldsymbol{u}^{n+1} $ではない.便宜上求めるこの速度$\boldsymbol{u}^{*}$を,仮速度や中間速度とよぶ.式(9)と式(10)の差を取ると,圧力勾配項の影響による速度の時間発展式が得られる.
\frac{\boldsymbol{u}^{n+1} - \boldsymbol{u}^*}{\Delta t} = -\frac{1}{\rho}\nabla p^{n+1} \qquad(11)
速度の時間発展を,式(10),(11)に分けることが,部分段階法の名前の由来である.$p^{n+1}$が判らないと,式(11)は計算できない.MAC法では,Navier-Stokes方程式の発散を計算したが,部分段階法では,式(11)の発散を計算する.
\frac{1}{\Delta t}(\nabla\cdot\boldsymbol{u}^{n+1} - \nabla\cdot\boldsymbol{u}^*) = -\frac{1}{\rho}\nabla^2 p^{n+1} \qquad(12)
$\boldsymbol{u}^*$は圧力の影響が入っていないので,連続の式は満たさないが,$\boldsymbol{u}^{n+1}$は連続の式を満たさなければならない.すなわち,$\nabla\cdot\boldsymbol{u}^{n+1}=0$である必要がある.そのためには,式(11)において
\frac{1}{\Delta t}\nabla\cdot\boldsymbol{u}^* - \frac{1}{\rho}\nabla^2 p^{n+1} =0
でなければならない.速度が関係する項を右辺に,圧力を左辺に置くと,これは時刻$n$における速度と圧力の関係を表すPoisson方程式となる.
\nabla^2 p^{n+1}=\frac{\rho}{\Delta t}\nabla\cdot\boldsymbol{u}^*\qquad(13)
これも圧力Poisson方程式とよばれる.
部分段階法では,$\boldsymbol{u}^n$が既知の時,次のような手順で流れ場の時間発展を計算する.
- 式(10)を用いて$\boldsymbol{u}^n$から中間速度$\boldsymbol{u}^*$を計算する.
- 式(13)を解いて,圧力$p^{n+1}$を計算する
- 式(12)を用いて$\boldsymbol{u}^{n+1}$を計算する.
MAC法を用いても,部分段階法を用いても,非圧縮性流体解析では圧力Poisson方程式からは逃れられない.連立方程式に変換された圧力Poisson方程式を解く時間は,非圧縮性流体解析の95%以上を締めるので,圧力Poisson方程式を高速に解くことは極めて意義が大きい.Poisson方程式を解く際の処理能力を測るベンチマークの重要性が知れよう.
差分法による空間の離散化
前節の圧力Poisson方程式は,時間のみを離散化しており,空間に微分については離散化をしていなかった.
姫野ベンチマークでは,空間微分を差分法によって離散化することで得られる離散的なPoisson方程式を計算する.
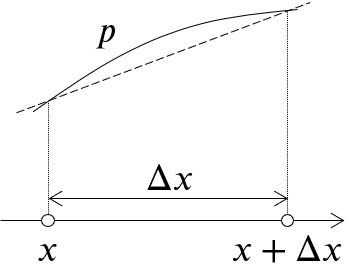
差分法は,例えば次式で表されるような微分
\frac{\partial p}{\partial x} = \lim_{\Delta x \rightarrow 0}\frac{p(x+\Delta x)- p(x)}{\Delta x}
において,無限小より大きいが$p$の変化に対して十分小さいような$\Delta x$を採用し,単純な割り算で近似する.
\frac{\partial p}{\partial x} \approx \frac{p(x+\Delta x)- p(x)}{\Delta x}
ここで,$p(x)$や$p(x+\Delta x)$と書くのが煩わしいので,$x$や$x+\Delta x$といった離散的な点に番号をつけ,それを一般的に$i$と書くことにする.$i$はindexの略である.$i$番目の点に定義された物理量(たとえば$p$)を表す際は,番号を下付添字で付与する.つまり,$p(x)$や$p(x+\Delta x)$は,それぞれ$p_i$や$p_{i+1}$と書く.
2階微分も同様にして近似する.
\frac{\partial^2 p}{\partial x^2} \approx \frac{\left.\frac{\partial p}{\partial x}\right|_{x+\Delta x/2}-\left.\frac{\partial p}{\partial x}\right|_{x-\Delta x/2}}{\Delta x}=\frac{1}{\Delta x}\left(\frac{p_{i+1}-p_i}{\Delta x}-\frac{p_i-p_{i-1}}{\Delta x}\right)=\frac{p_{i+1}-2p_i+p_{i-1}}{\Delta x^2}
圧力Poisson方程式の直交座標系での離散化
式(6)あるいは式(13)を離散化する.このとき,本稿の目的が具体的な流体解析の式を示すことではなく,姫野ベンチマークの説明であることを思い出してほしい.重要なのは式(6), (13)に共通に現れる圧力のラプラシアンの離散化である.姫野ベンチマークの実装では,右辺はwrk1という配列にまとめられているため,姫野ベンチマークの実装を理解する上で,右辺の離散化された形を導く必要はない.
圧力のラプラシアンは,$\nabla$を使う形で書かれているが,姫野ベンチマークでは直交座標系を想定している.直交座標系で表示する方が素直であるし,製造業の実務で行われるシミュレーションも直交座標系が非常に多い.
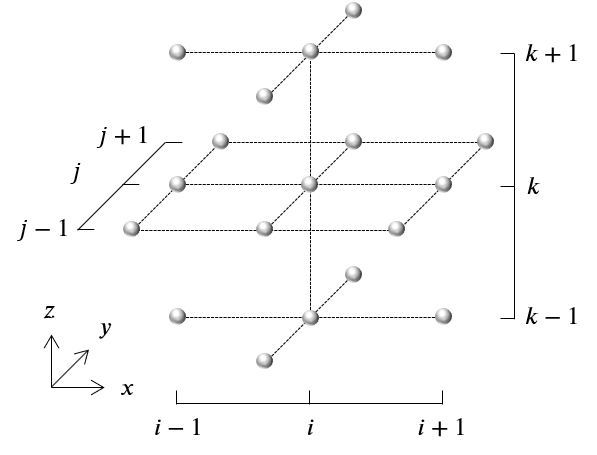
直交座標系($x-y-z$座標系)では圧力のラプラシアンは
\nabla^2 p = \frac{\partial^2 p}{\partial x^2} + \frac{\partial^2 p}{\partial y^2}+\frac{\partial^2 p}{\partial z^2}\qquad(14)
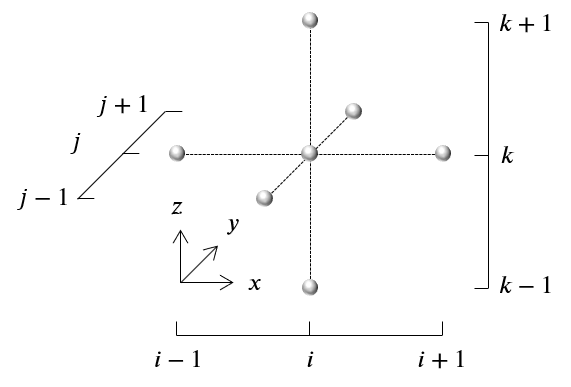
と書き下される.空間をスタガード格子に分割し,圧力を各セルの中心で定義する.各軸方向のセルの幅を$\Delta x, \Delta y, \Delta z$とすると,式(14)は次式のように離散化される.
\nabla^2 p \approx \frac{p_{i+1,j,k}-2p_{i,j,k}+p_{i-1,j,k}}{\Delta x ^2}+\frac{p_{i,j+1,k}-2p_{i,j,k}+p_{i,j-1,k}}{\Delta y ^2}+\frac{p_{i,j,k+1}-2p_{i,j,k}+p_{i,j,k-1}}{\Delta z ^2}\qquad(15)
式(15)は合計で7点の圧力を使うので,7点ステンシルなどと表現される.
一般座標系での離散化
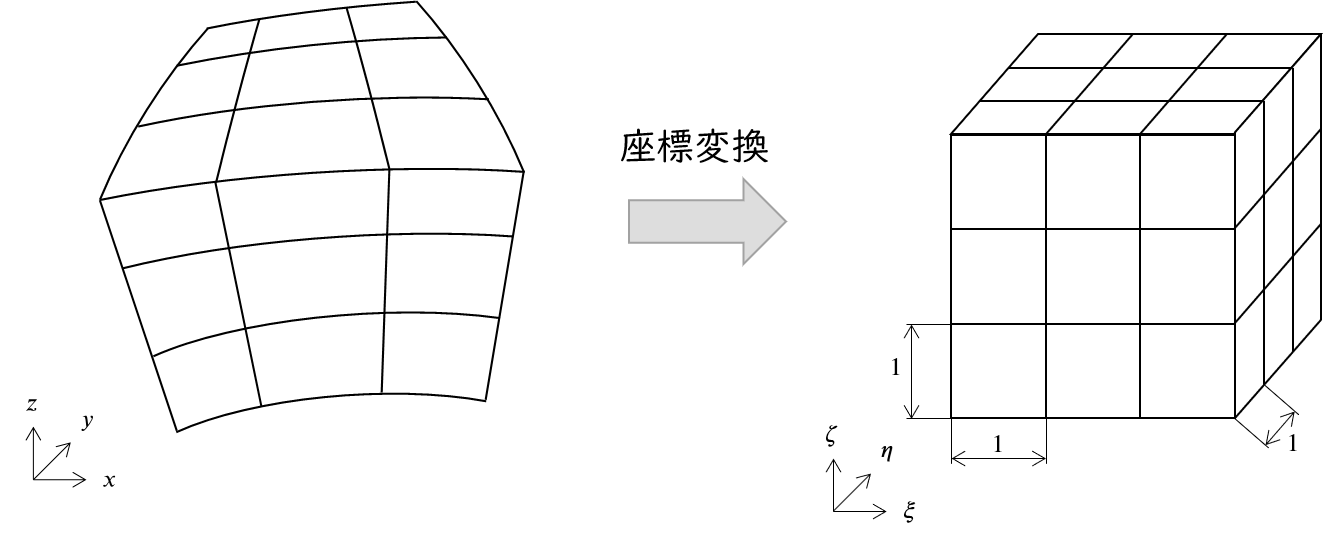
式(15)では,$\Delta x, \Delta y, \Delta z$は,それぞれ一定であることが要求される($\Delta x, \Delta y, \Delta z$の値は異なっていてもよい).そのため,式(15)のような離散化は,複雑な形状をもつ物体を表現しにくい.これは差分法の欠点であるが,差分法で任意の形状を表現できないわけではなく,座標変換を用いることでその欠点を解消できる.
複雑な形を表現するために,$x-y-z$座標系において,複雑な形をした格子を生成する.(例えば参考文献中の図5)その後,複雑な形状をした格子を,座標変換によって直交する格子に変換する.このとき,一つのセルは1辺の長さが$1$の立方体に変換する.座標変換後の系を$\xi-\eta-\zeta$座標系と書く.
いったん座標変換できると,$\xi-\eta-\zeta$系はセルの幅が1なので,微分は簡単に計算できる.しかし,微分した結果はあくまで$\xi-\eta-\zeta$系での微分 $\partial^2 p/\partial \xi^2, \partial^2 p/\partial \eta^2, \partial^2 p/\partial \zeta^2$ でしかないので,これを$x-y-z$座標系での微分と対応付けしなければならない.
連鎖則を用いて$x, y, z$についての微分と$\xi, \eta, \zeta$についての微分を対応させる.それらを行列の形でまとめて表すと,次のようになる.
\left(
\begin{matrix}
\frac{\partial }{\partial x}\\
\frac{\partial }{\partial y}\\
\frac{\partial }{\partial z}
\end{matrix}
\right)
=
\left(
\begin{matrix}
\frac{\partial \xi}{\partial x}&\frac{\partial \eta}{\partial x}&\frac{\partial \zeta}{\partial x}\\
\frac{\partial \xi}{\partial y}&\frac{\partial \eta}{\partial y}&\frac{\partial \zeta}{\partial y}\\
\frac{\partial \xi}{\partial z}&\frac{\partial \eta}{\partial z}&\frac{\partial \zeta}{\partial z}\\
\end{matrix}
\right)
\left(
\begin{matrix}
\frac{\partial }{\partial \xi}\\
\frac{\partial }{\partial \eta}\\
\frac{\partial }{\partial \zeta}
\end{matrix}
\right)\qquad(16)
とりあえず係数行列を$\boldsymbol{A}$と書くことにする.$\boldsymbol{A}$の要素$A_{i,j}$が計算できれば,$\xi-\eta-\zeta$系で微分した$p$とかけ算することで,$x-y-z$系へ変換できる. しかし,$x,y,z$による微分は,格子が複雑で難しいから座標変換しようとしているのであるから,変換の係数に$x,y,z$による微分が出てきては意味がない.そこで,式(10)と同様に$x-y-z$系を$\xi-\eta-\zeta$系に変換する式を考え,その係数行列の逆行列を利用する.
\left(
\begin{matrix}
\frac{\partial }{\partial \xi}\\
\frac{\partial }{\partial \eta}\\
\frac{\partial }{\partial \zeta}
\end{matrix}
\right)
=
\left(
\begin{matrix}
\frac{\partial x}{\partial \xi}&\frac{\partial y}{\partial \xi}&\frac{\partial z}{\partial \xi}\\
\frac{\partial x}{\partial \eta}&\frac{\partial y}{\partial \eta}&\frac{\partial z}{\partial \eta}\\
\frac{\partial x}{\partial \zeta}&\frac{\partial y}{\partial \zeta}&\frac{\partial z}{\partial \zeta}\\
\end{matrix}
\right)
\left(
\begin{matrix}
\frac{\partial }{\partial x}\\
\frac{\partial }{\partial y}\\
\frac{\partial }{\partial z}
\end{matrix}
\right)\qquad(17)
係数行列を$\boldsymbol{B}$と書き,その逆行列を左からをかけると,
\left(
\begin{matrix}
\frac{\partial }{\partial x}\\
\frac{\partial }{\partial y}\\
\frac{\partial }{\partial z}
\end{matrix}
\right)
=
\frac{1}{J}\boldsymbol{B}^{-1}
\left(
\begin{matrix}
\frac{\partial }{\partial \xi}\\
\frac{\partial }{\partial \eta}\\
\frac{\partial }{\partial \zeta}
\end{matrix}
\right)\qquad(18)
$J=\mathrm{det}\boldsymbol{B}$である.式(16)と式(18)の比較から$\boldsymbol{A} = \frac{1}{J}\boldsymbol{B}^{-1}$は明らかなので,$\boldsymbol{A}$の要素を$\xi-\eta-\zeta$系の微分で置き換えることができる.
\begin{align}
A_{1,1} &= \frac{1}{J}\left( \frac{\partial y}{\partial η}\frac{\partial z}{\partial ζ}-\frac{\partial y}{\partial ζ}\frac{\partial z}{\partial η}\right)\\
A_{1,2} &=-\frac{1}{J}\left( \frac{\partial y}{\partial ξ}\frac{\partial z}{\partial ζ}-\frac{\partial y}{\partial ζ}\frac{\partial z}{\partial ξ}\right)\\
A_{1,3} &= \frac{1}{J}\left( \frac{\partial y }{\partial ξ}\frac{\partial z}{\partial η}-\frac{\partial y}{\partial η}\frac{\partial z}{\partial ξ}\right)\\
A_{2,1} &=-\frac{1}{J}\left( \frac{\partial x}{\partial η}\frac{\partial z}{\partial ζ}-\frac{\partial x}{\partial ζ}\frac{\partial z}{\partial η}\right)\\
A_{2,2} &= \frac{1}{J}\left( \frac{\partial x}{\partial ξ}\frac{\partial z}{\partial ζ}-\frac{\partial x}{\partial ζ}\frac{\partial z}{\partial ξ}\right)\\
A_{2,3} &=-\frac{1}{J}\left( \frac{\partial x}{\partial ξ}\frac{\partial z}{\partial η}-\frac{\partial x}{\partial η}\frac{\partial z}{\partial ξ}\right)\\
A_{3,1} &= \frac{1}{J}\left( \frac{\partial x}{\partial ζ}\frac{\partial y}{\partial η}+\frac{\partial x}{\partial η}\frac{\partial y}{\partial ζ}\right)\\
A_{3,2} &=-\frac{1}{J}\left( \frac{\partial x}{\partial ξ}\frac{\partial y}{\partial ζ}-\frac{\partial x}{\partial ζ}\frac{\partial y}{\partial ξ}\right)\\
A_{3,3} &= \frac{1}{J}\left(\frac{\partial x}{\partial ξ}\frac{\partial y}{\partial η}-\frac{\partial x}{\partial η}\frac{\partial y}{\partial ξ}\right)
\end{align}
以降では,記述の都合上,$\boldsymbol{A}$の要素$A_{i,j}$を用いて式を展開するが,実際にプログラムを組む際は,それらを$(\frac{1}{J}{\boldsymbol{B}^{-1}})_{i,j}$に置き換える必要がある.
2階微分の式は,1階微分を2回行うことで導出する.
\left(
\begin{matrix}
p_x\\
p_y\\
p_z
\end{matrix}
\right)
=
\boldsymbol{A}
\left(
\begin{matrix}
\frac{\partial p}{\partial \xi}\\
\frac{\partial p}{\partial \eta}\\
\frac{\partial p}{\partial \zeta}
\end{matrix}
\right)
=
\left(
\begin{matrix}
A_{1,1}\frac{\partial p}{\partial \xi}+A_{1,2}\frac{\partial p}{\partial \eta}+A_{1,3}\frac{\partial p}{\partial \zeta}\\
A_{2,1}\frac{\partial p}{\partial \xi}+A_{2,2}\frac{\partial p}{\partial \eta}+A_{2,3}\frac{\partial p}{\partial \zeta}\\
A_{3,1}\frac{\partial p}{\partial \xi}+A_{3,2}\frac{\partial p}{\partial \eta}+A_{3,3}\frac{\partial p}{\partial \zeta}\\
\end{matrix}
\right)
\left(
\begin{matrix}
\frac{\partial^2 p}{\partial x^2}\\
\frac{\partial^2 p}{\partial y^2}\\
\frac{\partial^2 p}{\partial z^2}
\end{matrix}
\right)
=
\boldsymbol{A}
\left(
\begin{matrix}
\frac{\partial p_x}{\partial \xi}\\
\frac{\partial p_y}{\partial \eta}\\
\frac{\partial p_z}{\partial \zeta}
\end{matrix}
\right)
=
\left(
\begin{matrix}
A_{1,1}\frac{\partial p_x}{\partial \xi}+A_{1,2}\frac{\partial p_x}{\partial \eta}+A_{1,3}\frac{\partial p_x}{\partial \zeta}\\
A_{2,1}\frac{\partial p_y}{\partial \xi}+A_{2,2}\frac{\partial p_y}{\partial \eta}+A_{2,3}\frac{\partial p_y}{\partial \zeta}\\
A_{3,1}\frac{\partial p_z}{\partial \xi}+A_{3,2}\frac{\partial p_z}{\partial \eta}+A_{3,3}\frac{\partial p_z}{\partial \zeta}\\
\end{matrix}
\right)
これを真面目に展開するのは非常に骨が折れる.難しくはないが量が多い計算を注意深く行うことによって,次のような式が得られる.
\begin{align}
&\frac{\partial^2 p}{\partial x^2} + \frac{\partial^2 p}{\partial y^2} + \frac{\partial^2 p}{\partial z^2}\\
=&
\alpha_1 \frac{\partial^2 p}{\partial \xi^2} + \alpha_2 \frac{\partial p^2}{\partial \eta^2} + \alpha_3\frac{\partial^2 p}{\partial \zeta^2}
+ \alpha_4\frac{\partial^2 p}{\partial \xi \partial \eta} + \alpha_5\frac{\partial^2 p}{\partial \xi\partial \zeta} + \alpha_6\frac{\partial^2 p}{\partial \eta \partial \zeta}
+ \alpha_7\frac{\partial p}{\partial \xi} + \alpha_8\frac{\partial p}{\partial \eta} + \alpha_9\frac{\partial p}{\partial \zeta}\\
=&RHS\qquad(19)
\end{align}
$\alpha$は係数,$RHS$は$\xi-\eta-\zeta$系で記述された式(6)の右辺である.
式(19)を差分法により離散化する.$\Delta\xi=\Delta\eta=\Delta\zeta=1$であることを考慮すると,
\begin{align}
&\alpha_1 (p_{i+1,j,k}-2p_{i,j,k}+p_{i-1,j,k}) + \alpha_2 (p_{i,j+1,k}-2p_{i,j,k}+p_{i,j-1,k}) + \alpha_3 (p_{i,j,k+1}-2p_{i,j,k}+p_{i,j,k-1})\\
&+\alpha_4\frac{(p_{i+1,j+1,k}-p_{i-1,j+1,k})-(p_{i+1,j-1,k}-p_{i-1,j-1,k})}{4}\\
&+\alpha_5\frac{(p_{i+1,j,k+1}-p_{i-1,j,k+1})-(p_{i+1,j,k-1}-p_{i-1,j,k-1})}{4}\\
&+\alpha_6\frac{(p_{i,j+1,k+1}-p_{i,j-1,k+1})-(p_{i,j+1,k-1}-p_{i,j-1,k-1})}{4}\\
&+\alpha_7\frac{p_{i+1,j,k}-p_{i-1,j,k}}{2}
+\alpha_8\frac{p_{i,j+1,k}-p_{i,j-1,k}}{2}
+\alpha_9\frac{p_{i,j,k+1}-p_{i,j,k-1}}{2}=RHS_{i,j,k}.\qquad(20)
\end{align}
式(20)を展開し,$p$の添字が同一の項をまとめると,次式のように簡略化される.ただし,1回しか登場しない項は,係数でまとめられている.
\begin{align}
-2(\alpha_1+\alpha_2+\alpha_3)&p_{i,j,k}\\
+(\alpha_1+\frac{\alpha_7}{2})&p_{i+1,j,k}\\
+(\alpha_2+\frac{\alpha_8}{2})&p_{i,j+1,k}\\
+(\alpha_3+\frac{\alpha_9}{2})&p_{i,j,k+1}\\
+(\alpha_1-\frac{\alpha_7}{2})&p_{i-1,j,k}\\
+(\alpha_2-\frac{\alpha_8}{2})&p_{i,j-1,k}\\
+(\alpha_3-\frac{\alpha_9}{2})&p_{i,j,k-1}\\
+\frac{\alpha_4}{4}&(p_{i+1,j+1,k}-p_{i-1,j+1,k}-p_{i+1,j-1,k}+p_{i-1,j-1,k})\\
+\frac{\alpha_5}{4}&(p_{i+1,j,k+1}-p_{i-1,j,k+1}-p_{i+1,j,k-1}+p_{i-1,j,k-1})\\
+\frac{\alpha_6}{4}&(p_{i,j+1,k+1}-p_{i,j-1,k+1}-p_{i,j+1,k-1}+p_{i,j-1,k-1})=RHS_{i,j,k}\qquad(21)
\end{align}
$x-y-z$系では7点ステンシルであったが,座標変換を行うことによって交差微分が現れるため,$\xi-\eta-\zeta$系では19点ステンシルとなる.
計算の過程で格子が変化しなければこの係数$\alpha$も変化しないので,配列に代入しておけば計算量を減らすことができる.
\begin{align}
a_{i,j,k,1} &= \alpha_1+\frac{\alpha_7}{2}\\
a_{i,j,k,2} &= \alpha_2+\frac{\alpha_8}{2}\\
a_{i,j,k,3} &= \alpha_3+\frac{\alpha_9}{2}\\
a_{i,j,k,4} &= \frac{1}{2(\alpha_1+\alpha_2+\alpha_3)}\\
b_{i,j,k,1} &= \frac{\alpha_4}{4}\\
b_{i,j,k,2} &= \frac{\alpha_5}{4}\\
b_{i,j,k,3} &= \frac{\alpha_6}{4}\\
c_{i,j,k,1} &= \alpha_1-\frac{\alpha_7}{2}\\
c_{i,j,k,2} &= \alpha_2-\frac{\alpha_8}{2}\\
c_{i,j,k,3} &= \alpha_3-\frac{\alpha_9}{2}
\end{align}
姫野ベンチマークの実装に沿って名前および配列添字をつけている.これを反映すると,姫野ベンチマークで計算する圧力Poisson方程式は次式となる.
\begin{align}
&-\frac{1}{a_{i,j,k,4}}p_{i,j,k}
+a_{i,j,k,1} p_{i+1,j,k}
+a_{i,j,k,2} p_{i,j+1,k}
+a_{i,j,k,3} p_{i,j,k+1}\\
&+b_{i,j,k,1}(p_{i+1,j+1,k}-p_{i-1,j+1,k}-p_{i+1,j-1,k}+p_{i-1,j-1,k})\\
&+b_{i,j,k,2}(p_{i+1,j,k+1}-p_{i-1,j,k+1}-p_{i+1,j,k-1}+p_{i-1,j,k-1})\\
&+b_{i,j,k,3}(p_{i,j+1,k+1}-p_{i,j-1,k+1}-p_{i,j+1,k-1}+p_{i,j-1,k-1})\\
&+c_{i,j,k,1} p_{i-1,j,k}
+c_{i,j,k,2} p_{i,j-1,k}
+c_{i,j,k,3} p_{i,j,k-1} = RHS_{i,j,k}\qquad(22)
\end{align}
$RHS_{i,j,k}$は,$\xi-\eta-\zeta$系で離散化された式(6)の右辺の計算結果を格納した配列である.
圧力Poisson方程式の計算
式(22)を$p_{i,j,k}=...$の形に変形しても,$p_{i,j,k}$は周囲18点の圧力を参照しているため簡単には計算できない.圧力Poisson方程式は速度$\boldsymbol{u}^n$と圧力$p^n$が空間全体で満たすべき関係を記述しており,空間の全点における$p$についての連立一次方程式を解かなければならない.姫野ベンチマークでは,連立一次方程式を解くためにJacobi法が用いられている.
Jacobi法は連立一次方程式に対する反復解法の一つであり,未知数に適当な初期値を与え,未知数が連立方程式を満足するまで未知数を修正する.
1次元問題によるJacobi法の説明
Jacobi法の計算過程を,簡単な1次元のLaplace方程式を例に説明する.
\frac{\partial^2 p}{\partial x^2} = 0
計算領域の長さ$L_x$を$4$とし,境界条件として,$p(0)=0, p(L_x) = 1$を与える.
$L_x$を4等分し,差分法によって離散化すると,5個の離散点に対して5本の式を立てることができる.
\left\{\begin{align}
p_1 &= 0\\
\frac{p_1-2p_2+p_3}{\varDelta x^2} &= 0\\
\frac{p_2-2p_3+p_4}{\varDelta x^2} &= 0\\
\frac{p_3-2p_4+p_5}{\varDelta x^2} &= 0\\
p_5 &= 1
\end{align}\right.\qquad(23)
$\Delta x=1$を考慮して,式(23)を行列を使って書き直すと,次式のようになる.
\left(\begin{matrix}
1 & 0 & 0 & 0 & 0\\
1 &-2 & 1 & 0 & 0\\
0 & 1 &-2 & 1 & 0\\
0 & 0 & 1 &-2 & 1\\
0 & 0 & 0 & 0 & 1\\
\end{matrix}\right)
\left(\begin{matrix}
p_1 \\
p_2 \\
p_3 \\
p_4 \\
p_5 \\
\end{matrix}\right)
=
\left(\begin{matrix}
0 \\
0 \\
0 \\
0 \\
1 \\
\end{matrix}\right)\qquad(24)
簡略化して,$\boldsymbol{Ax}=\boldsymbol{b}$と書かれることもある.$\boldsymbol{A}$が係数行列,$\boldsymbol{x}$が未知ベクトル,$\boldsymbol{b}$が右辺ベクトルである.
Jacobi法は,反復法の一種であり,Gaussの消去法のように式(24)の係数行列を変形するのではなく,式(24)が満たされるように未知数$p_1$~$p_5$の値を更新する.
式(23)を
\left\{\begin{align}
p_1 &= 0\\
p_2 &= 0 + (p_1+p_3)/2\\
p_3 &= 0 + (p_2+p_4)/2 \\
p_4 &= 0 + (p_3+p_5)/2 \\
p_5 &= 1
\end{align}\right.\qquad(25)
と変形し,$p_2,p_3,p_4$に適当な値を入れて式(25)を計算する.
繰り返しの回数を右肩に括弧でくくって表示すると,次のような手順で$p_1$~$p_5$を更新していくことになる.
$0$は右辺(Poisson方程式の場合は非ゼロになる),$p_2^{(0)}, p_3^{(0)}, p_4^{(0)}$は初期値である.
\begin{align}
p_2^{(1)} &= 0 + (p_1+p_3^{(0)})/2\\
p_3^{(1)} &= 0 + (p_2^{(0)}+p_4^{(0)})/2 \\
p_4^{(1)} &= 0 + (p_3^{(0)}+p_5)/2 \\
\end{align}
\begin{align}
p_2^{(2)} &= 0 + (p_1+p_3^{(1)})/2\\
p_3^{(2)} &= 0 + (p_2^{(1)}+p_4^{(1)})/2 \\
p_4^{(2)} &= 0 + (p_3^{(1)}+p_5)/2 \\
\end{align}
\begin{align}
p_2^{(3)} &= 0 + (p_1+p_3^{(2)})/2\\
p_3^{(3)} &= 0 + (p_2^{(2)}+p_4^{(2)})/2 \\
p_4^{(3)} &= 0 + (p_3^{(2)}+p_5)/2 \\
\end{align}
この手順を繰り返す.Jacobi法では,繰返し回数を決めて所定の回数を繰り返すか,繰返し回数を決めず(上限は決めるが),計算途中の近似解$p_i^{(m)}$が一定の基準を満たすまで繰り返すやり方がある.近似解と正解の近さの評価には,残差を用いる方法と,変化量を用いる方法がある.
残差は,式(24)を$\boldsymbol{r}=\boldsymbol{b}-\boldsymbol{Ax}$と変形し,$\boldsymbol{x}$に$p_i^{(m)}$を代入して計算する.$\boldsymbol{r}$が残差であり,予め決めた値よりも残差が小さくなるまで計算を繰り返す.変化量は,$(m)$回目の繰り返しで得られた$p_i^{(m)}$と$(m+1)$回目の繰り返しで得られた$p_i^{(m+1)}$を比較し,その変化量が小さいと,$p_i$がこれ以上更新されない=正解に近いと判断する.
詳しくは後述するが,姫野ベンチマークでは,Jacobi法の繰り返し計算が60秒間実行されるように繰返し回数が決められるが,変化量も同時に計算される.ただし,変化量は繰返し回数に影響しない.
Jacobi法による圧力Poisson方程式の計算
姫野ベンチマークでは,圧力Poisson方程式をJacobi法を用いて計算する.1次元Laplace方程式の例と同様に,式(22)を$p_{i,j,k}=...$の形に変形する.
\begin{align}
p^{(m+1)}_{i,j,k} &= a_{i,j,k,4}s_{i,j,k}^{(m)}\qquad(26)\\
s_{i,j,k}^{(m)} &= a_{i,j,k,1} p^{(m)}_{i+1,j,k}
+a_{i,j,k,2} p^{(m)}_{i,j+1,k}
+a_{i,j,k,3} p^{(m)}_{i,j,k+1}\\
&+b_{i,j,k,1}(p^{(m)}_{i+1,j+1,k}-p^{(m)}_{i-1,j+1,k}-p^{(m)}_{i+1,j-1,k}+p^{(m)}_{i-1,j-1,k})\\
&+b_{i,j,k,2}(p^{(m)}_{i+1,j,k+1}-p^{(m)}_{i-1,j,k+1}-p^{(m)}_{i+1,j,k-1}+p^{(m)}_{i-1,j,k-1})\\
&+b_{i,j,k,3}(p^{(m)}_{i,j+1,k+1}-p^{(m)}_{i,j-1,k+1}-p^{(m)}_{i,j+1,k-1}+p^{(m)}_{i,j-1,k-1})\\
&+c_{i,j,k,1} p^{(m)}_{i-1,j,k}
+c_{i,j,k,2} p^{(m)}_{i,j-1,k}
+c_{i,j,k,3} p^{(m)}_{i,j,k-1} + wrk1_{i,j,k}\qquad(27)
\end{align}
$p_{i,j,k}$以外の項を右辺に移項し,両辺を$-1/a_{i,j,k,4}$で除している.そのため,右辺ベクトル$RHS_{i,j,k}$にマイナスが付いている.右辺ベクトルにマイナス符号を書けた値を,姫野ベンチマークの実装にあわせて$wrk1_{i,j,k}(=-RHS_{i,j,k})$と置いている.
圧力の値を反復の初期値として,$m=0$からすべての$i,j,k$について式を計算し,その後$p^{(m+1)}$が式を満たしているかを評価し,満たしているなら$p^n = p^{(m+1)}$とする.満たしていないならさらに反復を繰り返す.
初期設定
圧力の初期値は,サブルーチンinitmtで与えられている.
do k=1,kmax
p(:,:,k)=real((k-1)*(k-1),4)/real((kmax-1)*(kmax-1),4)
enddo
pは,x-y平面で一定,z方向に0から1の範囲で徐々に変化するように与えられている.
real(value, kind)はFortranの組込関数であり,valueをkindで指定した精度の実数に変換する.多くのFortranコンパイラでは,kind=4が単精度,kind=8が倍精度を意味するが,これは規格で決まっているわけではないので,Fortran 2008から追加された定数real32, real64を使うべきである.
また,initmtでは,係数a, b, cも初期化されている.
a=0.0
b=0.0
c=0.0
p=0.0
bnd=0.0
!
a(1:imax,1:jmax,1:kmax,1:3)=1.0
a(1:imax,1:jmax,1:kmax,4)=1.0/6.0
c(1:imax,1:jmax,1:kmax,:)=1.0
bnd(1:imax,1:jmax,1:kmax)=1.0
bndはBoundary Flagであり,境界より内側で1,境界で0と定義されている.姫野ベンチマークでは,全て1で初期化されている.
Jacobi法の実装
姫野ベンチマークの主要な処理であるJacobi法による繰り返し計算は,サブルーチンjacobiで行われている.
以下の箇所が式(27)に相当する.
do k=2,kmax-1
do j=2,jmax-1
do i=2,imax-1
s0=a(I,J,K,1)*p(I+1,J,K) &
+a(I,J,K,2)*p(I,J+1,K) &
+a(I,J,K,3)*p(I,J,K+1) &
+b(I,J,K,1)*(p(I+1,J+1,K)-p(I+1,J-1,K) &
-p(I-1,J+1,K)+p(I-1,J-1,K)) &
+b(I,J,K,2)*(p(I,J+1,K+1)-p(I,J-1,K+1) &
-p(I,J+1,K-1)+p(I,J-1,K-1)) &
+b(I,J,K,3)*(p(I+1,J,K+1)-p(I-1,J,K+1) &
-p(I+1,J,K-1)+p(I-1,J,K-1)) &
+c(I,J,K,1)*p(I-1,J,K) &
+c(I,J,K,2)*p(I,J-1,K) &
+c(I,J,K,3)*p(I,J,K-1)+wrk1(I,J,K)
! 誤差の計算は省略
enddo
enddo
enddo
wrk1(I,J,K)が$wrk1_{i,j,k}(=-RHS_{i,j,k})$である.
姫野ベンチマークでは,式(6)を満たしているかを評価するために,繰り返し計算前後の圧力の値の差$\varepsilon$を計算し,その2乗の総和を計算している.
\begin{align}
\varepsilon_{i,j,k} &= p_{i,j,k}^{(m+1)} - p^{(m)}_{i,j,k}\\
&= a_{i,j,k,4}s_{i,j,k}^{(m)} - p^{(m)}_{i,j,k}\qquad(28)\\
\varepsilon &= \sum_{i,j,k}\varepsilon_{i,j,k}^2\qquad(29)
\end{align}
ss=(s0*a(I,J,K,4)-p(I,J,K))*bnd(I,J,K)
GOSA=GOSA+SS*SS
これは1反復あたりの圧力の変化量を計算していることに相当しており,反復の過程で圧力が変化しなくなれば,それは式(6)を満足している状態と判断できる.また,十分な繰り返し計算が行われた結果,$p^{(m+1)}$が時刻$n$における圧力$p^n$と等しくなったとすると,式(28)は誤差と見なすことができるので,誤差の2乗和を求めていると見なせる.
変化量$\varepsilon_{i,j,k}$を求めた後,圧力が更新される.変化量にはBoundary Flag(bnd)がかけられている.Boundary Flagは境界内部で1,境界で0と定義されており,境界内部であれば圧力変化を反映し,境界であれば圧力変化を反映させないようにしている.実用的な計算では,計算領域内に物体が置かれることもあり,そのような場合に有効に機能する.
圧力を更新する際は,変化量に緩和係数$\omega$がかけられている.姫野ベンチマークでは緩和係数として0.8が用いられており,変化量を0.8倍しているので,これを減速緩和とよぶ.
p^{(m+1)}_{i,j,k} = p^{(m)}_{i,j,k} + \omega*\varepsilon_{i,j,k}
実装では,反復の過程で$p^{(m+1)}$と$p^{(m)}$が混在しないように,$p^{(m+1)}$は一度別の配列(wrk2)に代入される.更新すべき点((2:imax-1, 2:jmax-1, 2:kmax-1))の$p^{(m+1)}$を計算し終わった後,一括で配列p代入される.
do k=2,kmax-1
do j=2,jmax-1
do i=2,imax-1
...
ss=(s0*a(I,J,K,4)-p(I,J,K))*bnd(I,J,K)
GOSA=GOSA+SS*SS
wrk2(I,J,K)=p(I,J,K)+OMEGA *SS
enddo
enddo
enddo
p(2:imax-1,2:jmax-1,2:kmax-1)= &
wrk2(I,J,K)=p(I,J,K)+OMEGA *SS
本来であれば,圧力を更新した後に誤差を評価し,それが規定の誤差よりも小さければ反復を終了する.姫野ベンチマークでは,実行時間がおよそ60秒になるように反復回数nnが決められるので,そのような収束判定はプログラム中に現れない.
do loop=1,nn
gosa= 0.0
do k=2,kmax-1
do j=2,jmax-1
do i=2,imax-1
...
enddo
enddo
enddo
p(2:imax-1,2:jmax-1,2:kmax-1)= &
wrk2(2:imax-1,2:jmax-1,2:kmax-1)
enddo
姫野ベンチマークの処理の流れ
姫野ベンチマークは,他のベンチマーク問題のように問題を解く時間を計るのではなく,約60秒間Jacobi法による繰り返し計算を行い,計算量と時間からFLOPS値を推定する.
そのため,姫野ベンチマークは処理の流れが少し特殊である.姫野ベンチマークの処理の流れは下記の通りである.
- 計算問題の規模(XS, S, M, L, XL)をキーボード入力し,それに基づいて格子点数を決定する.サブルーチン
readparamおよびgrid_setで行われる. - 圧力や係数などの配列を動的に割り付ける.サブルーチン
initmemで行われる. - 割り付けた配列を初期化する.サブルーチン
initmtで行われる. -
system_clockを呼出し,時間測定の精度(時間分解能)を調査する. - Jacobi法の繰返し回数
nnを3回に設定し,サブルーチンjacobiの実行に要した時間を測定する.これはリハーサル測定とよばれている. - FLOPS値を出力すると共に,Jacobi法の繰り返し計算を60秒間実行するための繰返し回数
nnを計算する. - サブルーチン
jacobiを実行して実行時間を測定し,FLOPS値,実行時間,Pentimu III 600 MHzの性能に対する比を出力する.