概要
Twitterで話題に上がっていた問題に対して残差切除法12を適用した.復習がてら残差切除法の計算手順もまとめた.
対象問題
問題の詳細は
\frac{\partial^2 p}{\partial x^2} + \frac{\partial^2 p}{\partial y^2} = 1, 0\le x\le 1,0\le y\le 1
境界条件は
\begin{eqnarray}
\frac{\partial p}{\partial x} &=& 1, \text{at } x=0\\
\frac{\partial p}{\partial x} &=& 2, \text{at } x=1\\
\frac{\partial p}{\partial y} &=& 0, \text{at } y=0,1
\end{eqnarray}
である.これを,とりあえずP問題と呼ぶことにする.
境界条件がすべてノイマン境界条件なので,Poisson方程式の離散化手法や求解法によっては解けないことがある3.
問題は2次元だが,$y=0,1$で$y$方向に勾配0が与えられているので,解は$y$方向に一定で$x$の関数になる.そこで,問題を1次元化し,1次元化P問題を残差切除法によって解く.
\begin{eqnarray}
\frac{\partial^2 p}{\partial x^2} &=& 1, 0< x < 1\\
\frac{\partial p}{\partial x} &=& 1, \text{at } x=0\\
\frac{\partial p}{\partial x} &=& 2, \text{at } x=1
\end{eqnarray}
式を積分すると,
\begin{eqnarray}
\frac{\partial p}{\partial x} &=& x + C_1\\
p &=& \frac{1}{2}x^2 + C_1x + C_2
\end{eqnarray}
$C_1,C_2$は積分定数である.境界条件から$C_1=1$は求まるが,$C_2$を求めることはできない.
残差切除法
残差切除法1は,境界値問題に対する解法の一つであり,JAXAの研究者によって提案された.
離散化された方程式を解く際に,係数行列と右辺ベクトルから近似解を頑張って計算するのではなく,残差方程式を解いて修正量を求め,近似解を修正する.その点では,マルチグリッド法に近い方法といえる.マルチグリッド法では,Jacobi法系統の方法が高周波成分を効率よく減衰させることに着目し,残差方程式を粗い格子に写して解くことで,粗い格子における高周波成分(細かい格子では低周波成分)を減衰させる.一方で,残差切除法は,複数の反復ステップの修正量を利用して残差を減少させる.その際,残差を最小化するような係数を最小二乗法により計算する.残差切除法はill-posedな問題でも問題なく解けるらしいが,そのあたりはどういう問題に対して適用すれば確認できるのか,著者はよくわかっていない.
残差切除法のアルゴリズム1
Poisson方程式を離散化し,得られた式を行列の形で表示する.
\boldsymbol{D}\boldsymbol{p}=\boldsymbol{f}
境界条件は,ディリクレおよびノイマン境界条件が与えられているとする.
\begin{eqnarray}
p&=&p_b \text{ on Dirichlet boundary}\\
\frac{\partial p}{\partial n}&=&\Delta p_b \text{ on Neumann boundary}
\end{eqnarray}
ここで,$n$は境界の法線方向である.
摂動量の残差方程式
離散化されたPoisson方程式の近似解を,反復しながら徐々に真の解に近づける.反復のステップを$m$と表すと,$m$ステップにおける残差$\boldsymbol{r}$は次のように計算される.
\boldsymbol{r}^{(m)} = \boldsymbol{f} - \boldsymbol{D}\boldsymbol{p}^{(m)}
上付きの$(m)$は反復のステップを表している.
Poisson方程式の真の解$\boldsymbol{p}$と近似解$\boldsymbol{p}^{(m)}$の差を摂動量として$\boldsymbol{\phi}=\boldsymbol{p}-\boldsymbol{p}^{(m)}$と書き,離散化されたPoisson方程式に代入すると,摂動量の残差方程式が得られる.
\boldsymbol{D}\boldsymbol{\phi}=\boldsymbol{r}^{(m)}
近似解が境界条件を満足していれば,摂動量に対する境界条件は次のように与えられる.
\begin{eqnarray}
\phi&=&0 \text{ on Dirichlet boundary}\\
\frac{\partial \phi}{\partial n}&=&0 \text{ on Neumann boundary}
\end{eqnarray}
残差切除法では,離散化された残差方程式をきちんと解かない.残差方程式を粗く解いて近似値$\tilde{\boldsymbol{\phi}}$を求めた後,残差の$l_2$ノルムを最小にする合成摂動量$\boldsymbol{\phi}^{(m)}$を次の式で計算する.
\boldsymbol{\phi}^{(m)} = \alpha_1 \tilde{\boldsymbol{\phi}} + \sum_{l=2}^L\alpha_l\boldsymbol{\phi}^{(m-l+1)}
$\alpha_l$は残差最小化係数であり,全領域で一定である.
合成摂動量$\boldsymbol{\phi}^{(m)}$によって$\boldsymbol{p}^{(m-1)}$を修正し,修正した$\boldsymbol{p}^{(m)}$を用いて反復を繰り返す.
\boldsymbol{p}^{(m)} = \boldsymbol{p}^{(m-1)} + \boldsymbol{\phi}^{(m)}
残差最小化係数の計算
合成摂動量が$m+1$ステップでの残差を最小化するように残差最小化係数を決定する.$m+1$ステップにおける残差方程式
\boldsymbol{r}^{(m+1)}=\boldsymbol{f}-\boldsymbol{D}\boldsymbol{p}^{(m+1)}
に$m$ステップでの残差の式および$\boldsymbol{p}$の更新式を用いると,
\boldsymbol{r}^{(m+1)}=\boldsymbol{r}^{(m)} - \alpha_1 \boldsymbol{D}\tilde{\boldsymbol{\phi}} - \sum_{l=2}^L\alpha_l\boldsymbol{D}\boldsymbol{\phi}^{(m-l+1)}.
$\boldsymbol{r}^{(m+1)}$の$l_2$ノルム$||\boldsymbol{r}^{(m+1)}||$は,
||\boldsymbol{r}^{(m+1)}||=\sqrt{\sum_i\left(\boldsymbol{r}^{(m)} - \alpha_1 \boldsymbol{D}\tilde{\boldsymbol{\phi}} - \sum_{l=2}^L\alpha_l\boldsymbol{D}\boldsymbol{\phi}^{(m-l+1)}\right)_i^2}
として計算される.ここで,$()_i$は,括弧内の式を計算した結果の要素$i$を意味する.論文1では,当該箇所に
内点すべての総和の平方根として
と書いてあるので,境界は含まないと考えられる.つまり,本記事で対象とする問題では,$2\le i \le N_x-1$であろう.
残差切除法では,$||\boldsymbol{r}^{(m+1)}||$を最小化するように,最小二乗法を用いて残差最小化係数を決定する.
\frac{\partial ||\boldsymbol{r}^{(m+1)}||^2}{\partial \alpha_l}=0, l=1,2,\ldots,L
この式は$L$元連立方程式を作るので,それを解くことで$\alpha_l$が得られる.
対象問題への適用
1次元化P問題の計算に残差切除法を適用する.計算領域($L_x=1$)に5点の離散点($N_x = 5$)を設け,差分法によって式を離散化する.内点では2次精度中心差分,境界では2次精度の片側差分を用いる.残差最小化係数を3個用いる.すなわち,3元連立一次方程式を解いて$\alpha_1,\alpha_2,\alpha_3$を計算する.
まず,Poisson方程式を離散化する.
\begin{eqnarray}
\frac{p_{i+1}-2p_i+p_{i-1}}{\Delta x^2} &=& 1, i = 2,3,4\\
\frac{-3p_1+4p_2-p_3}{2\Delta x} &=& 1, i=1\\
\frac{ 3p_5-4p_4+p_3}{2\Delta x} &=& 2, i=5
\end{eqnarray}
行列の形で書くと
\frac{1}{\Delta x^2}\begin{pmatrix}
\frac{-3}{2}\Delta x & \frac{4}{2}\Delta x& \frac{-1}{2}\Delta x& & \\
1 & -2 & 1 & & \\
& 1 & -2 & 1 & \\
& & 1 & -2 & 1\\
& & \frac{1}{2}\Delta x & \frac{-4}{2}\Delta x & \frac{3}{2}\Delta x
\end{pmatrix}
\begin{pmatrix}
p_1\\
p_2\\
p_3\\
p_4\\
p_5
\end{pmatrix}
=
\begin{pmatrix}
1\\
1\\
1\\
1\\
2
\end{pmatrix}
同様に,残差方程式も離散化する.
\begin{eqnarray}
\frac{\phi_{i+1}-2\phi_i+\phi_{i-1}}{\Delta x^2} &=& r_i^{(m)}, i = 2,3,4\\
\frac{-3\phi_1+4\phi_2-\phi_3}{2\Delta x} &=& 0, i=1\\
\frac{ 3\phi_5-4\phi_4+\phi_3}{2\Delta x} &=& 0, i=5
\end{eqnarray}
ただし,境界で勾配0を与えるには,$p_i$の初期値$p_i^{(0)}$が境界条件を満足している必要がある.
行列の形で書くと
\frac{1}{\Delta x^2}\begin{pmatrix}
\frac{-3}{2}\Delta x & \frac{4}{2}\Delta x& \frac{-1}{2}\Delta x& & \\
1 & -2 & 1 & & \\
& 1 & -2 & 1 & \\
& & 1 & -2 & 1\\
& & \frac{1}{2}\Delta x & \frac{-4}{2}\Delta x & \frac{3}{2}\Delta x
\end{pmatrix}
\begin{pmatrix}
\phi_1\\
\phi_2\\
\phi_3\\
\phi_4\\
\phi_5
\end{pmatrix}
=
\begin{pmatrix}
0\\
r_2^{(m)}\\
r_3^{(m)}\\
r_4^{(m)}\\
0
\end{pmatrix}
初期値(m=0)
$p_i$の初期値は境界を除く全領域($i=2,3,4$)で0とし,それらの値を与えた後,$i=1,5$で境界条件を適用する.
\begin{eqnarray}
p_2^{(0)} &=& 0\\
p_3^{(0)} &=& 0\\
p_4^{(0)} &=& 0\\
p_1^{(0)} &=& \frac{2\Delta xf_1-4p_2^{(0)}+p_3^{(0)}}{-3}\\
p_5^{(0)} &=& \frac{2\Delta xf_5+4p_4^{(0)}-p_3^{(0)}}{3}
\end{eqnarray}
m=1
1.残差$r_i^{(1)}$を計算する.
\begin{eqnarray}
r_1^{(1)} &=& f_1 - \frac{-3p_1^{(0)}+4p_2^{(0)}-p_3^{(0)}}{2\Delta x}\\
r_2^{(1)} &=& f_2-\frac{p_3^{(0)}-2p_2^{(0)}+p_1^{(0)}}{\Delta x^2}\\
r_3^{(1)} &=& f_3-\frac{p_4^{(0)}-2p_3^{(0)}+p_2^{(0)}}{\Delta x^2}\\
r_4^{(1)} &=& f_4-\frac{p_5^{(0)}-2p_4^{(0)}+p_3^{(0)}}{\Delta x^2}\\
r_5^{(1)} &=& f_5 - \frac{3p_5^{(0)}-4p_4^{(0)}+p_3^{(0)}}{2\Delta x}
\end{eqnarray}
2.内部ソルバによって残差方程式を計算し,摂動量の近似値$\tilde{\phi_i}$を得る.ここでは,SOR法を用い,反復回数$N_{\text{ite}}$,加速係数$a$を適当に与えている.
3.残差最小化係数を計算する.
$||\boldsymbol{r}^{(2)}||^2=\sum_i(\boldsymbol{r}^{(1)} - \alpha_1 \boldsymbol{D}\tilde{\boldsymbol{\phi}})^2_i$ であるため,$\alpha_1$で微分すると,
\begin{eqnarray}
\frac{\partial ||\boldsymbol{r}^{(2)}||^2}{\partial \alpha_1} &=& \frac{\partial}{\partial \alpha_1}\sum_i(\boldsymbol{r}^{(1)} - \alpha_1 \boldsymbol{D}\tilde{\boldsymbol{\phi}})_i^2\\
&=&\sum_i[-2r_i^{(1)}(\boldsymbol{D}\tilde{\boldsymbol{\phi}})_i + 2\alpha_1 (\boldsymbol{D}\tilde{\boldsymbol{\phi}})_i^2]\\
&=&0
\end{eqnarray}
より
\alpha_1\sum_i(\boldsymbol{D}\tilde{\boldsymbol{\phi}})^2_i = \sum_ir_i^{(1)}(\boldsymbol{D}\tilde{\boldsymbol{\phi}})_i
が得られるので,2.で計算した$\tilde{\phi_i}$と係数行列$\boldsymbol{D}$の積を計算すればよい.$(\boldsymbol{D}\tilde{\boldsymbol{\phi}})^2_i$は,行列ベクトル積$\boldsymbol{D}\tilde{\boldsymbol{\phi}}$を計算した結果の$i$番目の要素の2乗である.
表記の簡略化のために中間変数$R_{1,i}$を導入すれば
R_{1,i} = \sum_{j}D_{i,j}\tilde{\boldsymbol{\phi}}_j\\
\alpha_1\sum_iR_{1,i}R_{1,i} = \sum_ir_i^{(1)}R_{1,i}
4.合成摂動量$\phi^{(1)}$を計算する
\phi_i^{(1)} = \alpha_1 \tilde{\phi_i}
5.$p$を更新する.上付き添字が残差切除法の節で示した添字と異なっているが,これは単に計算手順の都合であり,各自で対応関係を把握してもらいたい.
p_i^{(1)} = p_i^{(0)} + \phi_i^{(1)}
6.$p_i^{(1)}$を用いて残差を計算し,規定値以下になっていれば反復を終了する.
m=2
$m=2$でも計算手順は同じである.
1.残差$r_i^{(2)}$を計算する.
2.内部ソルバによって残差方程式を計算し,摂動量の近似値$\tilde{\phi_i}$を得る.
3.残差最小化係数を計算する.
$m=2$において,$\boldsymbol{r}^{(3)}$の$l_2$ノルムは$||\boldsymbol{r}^{(3)}||^2= \sum_i(\boldsymbol{r}^{(2)} - \alpha_1 \boldsymbol{D}\tilde{\boldsymbol{\phi}}-\alpha_2 \boldsymbol{D} \boldsymbol{\phi}^{(1)})_i^2$となる.
$\alpha_1$で微分すると,
\begin{eqnarray}
\frac{\partial ||\boldsymbol{r}^{(3)}||^2}{\partial \alpha_1}
&=& \sum_i[-2r_i^{(2)}(\boldsymbol{D} \tilde{\boldsymbol{\phi}})_i+2\alpha_1(\boldsymbol{D} \tilde{\boldsymbol{\phi}})_i^2+2\alpha_2(\boldsymbol{D} \tilde{\boldsymbol{\phi}})_i(\boldsymbol{D}\boldsymbol{\phi}^{(1)})_i]\\
&=&0.
\end{eqnarray}
おなじく$\alpha_2$で微分すると
\begin{eqnarray}
\frac{\partial ||\boldsymbol{r}^{(3)}||^2}{\partial \alpha_2}
&=& \sum_i[-2r_i^{(2)}(\boldsymbol{D}\boldsymbol{\phi}^{(1)})_i+2\alpha_1(\boldsymbol{D} \tilde{\boldsymbol{\phi}})_i(\boldsymbol{D}\boldsymbol{\phi}^{(1)})_i+2\alpha_2(\boldsymbol{D}\boldsymbol{\phi}^{(1)})_i^2]\\
&=&0.
\end{eqnarray}
$\alpha_l$について2元連立一次方程式を作ると,
\begin{pmatrix}
\sum_i(\boldsymbol{D} \tilde{\boldsymbol{\phi}})_i(\boldsymbol{D} \tilde{\boldsymbol{\phi}})_i & \sum_i(\boldsymbol{D} \tilde{\boldsymbol{\phi}})_i(\boldsymbol{D}\boldsymbol{\phi}^{(1)})_i\\
\sum_i(\boldsymbol{D}\boldsymbol{\phi}^{(1)})_i(\boldsymbol{D} \tilde{\boldsymbol{\phi}})_i &\sum_i(\boldsymbol{D}\boldsymbol{\phi}^{(1)})_i(\boldsymbol{D}\boldsymbol{\phi}^{(1)})_i
\end{pmatrix}
\begin{pmatrix}
\alpha_1\\
\alpha_2
\end{pmatrix}
=
\begin{pmatrix}
\sum_i r_i^{(2)}(\boldsymbol{D} \tilde{\boldsymbol{\phi}})_i\\
\sum_i r_i^{(2)}(\boldsymbol{D}\boldsymbol{\phi}^{(1)})_i
\end{pmatrix}
これを解いて$\alpha_1,\alpha_2$を得る.
中間変数$R_{1,i},R_{2,i}$を導入した簡略表記では,
\begin{eqnarray}
R_{1,i} &=& \sum_{j}D_{i,j}\tilde{\boldsymbol{\phi}}_j\\
R_{2,i} &=& \sum_{j}D_{i,j}\boldsymbol{\phi}_j^{(1)}
\end{eqnarray}
\begin{pmatrix}
\sum_iR_{1,i}R_{1,i} & \sum_iR_{1,i}R_{2,i}\\
\sum_iR_{2,i}R_{1,i} &\sum_iR_{2,i}R_{2,i}
\end{pmatrix}
\begin{pmatrix}
\alpha_1\\
\alpha_2
\end{pmatrix}
=
\begin{pmatrix}
\sum_i r_i^{(2)}R_{1,i}\\
\sum_i r_i^{(2)}R_{2,i}
\end{pmatrix}
4.合成摂動量$\phi^{(2)}$を計算する.
\phi_i^{(2)} = \alpha_1 \tilde{\phi_i} + \alpha_2 \phi_i ^{(1)}
5.$p$を更新する.
p_i^{(2)} = p_i^{(1)} + \phi_i^{(2)}
6.$p_i^{(2)}$を用いて残差を計算し,規定値以下になっていれば反復を終了する.
m=3
1.残差$r_i^{(3)}$を計算する.
2.内部ソルバによって残差方程式を計算し,摂動量の近似値$\tilde{\phi_i}$を得る.
3.残差最小化係数を計算する.
$\boldsymbol{r}^{(4)}$の$l_2$ノルムは$||\boldsymbol{r}^{(4)}||^2= \sum_i(\boldsymbol{r}^{(3)} - \alpha_1 \boldsymbol{D}\tilde{\boldsymbol{\phi}}-\alpha_2 \boldsymbol{D} \boldsymbol{\phi}^{(2)}-\alpha_3 \boldsymbol{D} \boldsymbol{\phi}^{(1)})_i^2$となる.
$\alpha_1$で微分すると,
\begin{eqnarray}
\frac{\partial ||\boldsymbol{r}^{(4)}||^2}{\partial \alpha_1}
&=& \sum_i[-2r_i^{(3)}(\boldsymbol{D} \tilde{\boldsymbol{\phi}})_i+2\alpha_1(\boldsymbol{D} \tilde{\boldsymbol{\phi}})_i^2+2\alpha_2(\boldsymbol{D} \tilde{\boldsymbol{\phi}})_i(\boldsymbol{D}\boldsymbol{\phi}^{(2)})_i+2\alpha_3(\boldsymbol{D} \tilde{\boldsymbol{\phi}})_i(\boldsymbol{D}\boldsymbol{\phi}^{(1)})_i]\\
&=&0.
\end{eqnarray}
$\alpha_2$で微分すると
\begin{eqnarray}
\frac{\partial ||\boldsymbol{r}^{(4)}||^2}{\partial \alpha_2}
&=& \sum_i[-2r_i^{(3)}(\boldsymbol{D}\boldsymbol{\phi}^{(2)})_i+2\alpha_1(\boldsymbol{D} \tilde{\boldsymbol{\phi}})_i(\boldsymbol{D}\boldsymbol{\phi}^{(2)})_i+2\alpha_2(\boldsymbol{D}\boldsymbol{\phi}^{(2)})_i^2+2\alpha_3(\boldsymbol{D} \boldsymbol{\phi}^{(1)})_i(\boldsymbol{D}\boldsymbol{\phi}^{(2)})_i]\\
&=&0.
\end{eqnarray}
$\alpha_3$で微分すると
\begin{eqnarray}
\frac{\partial ||\boldsymbol{r}^{(4)}||^2}{\partial \alpha_3}
&=& \sum_i[-2r_i^{(3)}(\boldsymbol{D}\boldsymbol{\phi}^{(1)})_i+2\alpha_1(\boldsymbol{D} \tilde{\boldsymbol{\phi}})_i(\boldsymbol{D}\boldsymbol{\phi}^{(1)})_i+2\alpha_2(\boldsymbol{D}\boldsymbol{\phi}^{(2)})_i(\boldsymbol{D}\boldsymbol{\phi}^{(1)})_i+2\alpha_3(\boldsymbol{D} \boldsymbol{\phi}^{(1)})_i^2]\\
&=&0.
\end{eqnarray}
$\alpha_l$について3元連立一次方程式を作ると,
\begin{pmatrix}
\sum_i(\boldsymbol{D} \tilde{\boldsymbol{\phi}})_i(\boldsymbol{D} \tilde{\boldsymbol{\phi}})_i & \sum_i(\boldsymbol{D} \tilde{\boldsymbol{\phi}})_i(\boldsymbol{D}\boldsymbol{\phi}^{(2)})_i& \sum_i(\boldsymbol{D} \tilde{\boldsymbol{\phi}})_i(\boldsymbol{D}\boldsymbol{\phi}^{(1)})_i\\
\sum_i(\boldsymbol{D}\boldsymbol{\phi}^{(2)})_i(\boldsymbol{D} \tilde{\boldsymbol{\phi}})_i &\sum_i(\boldsymbol{D}\boldsymbol{\phi}^{(2)})_i(\boldsymbol{D}\boldsymbol{\phi}^{(2)})_i&\sum_i(\boldsymbol{D}\boldsymbol{\phi}^{(2)})_i(\boldsymbol{D}\boldsymbol{\phi}^{(1)})_i\\
\sum_i(\boldsymbol{D}\boldsymbol{\phi}^{(1)})_i(\boldsymbol{D} \tilde{\boldsymbol{\phi}})_i &\sum_i(\boldsymbol{D}\boldsymbol{\phi}^{(1)})_i(\boldsymbol{D}\boldsymbol{\phi}^{(2)})_i&\sum_i(\boldsymbol{D}\boldsymbol{\phi}^{(1)})_i(\boldsymbol{D}\boldsymbol{\phi}^{(1)})_i
\end{pmatrix}
\begin{pmatrix}
\alpha_1\\
\alpha_2\\
\alpha_3
\end{pmatrix}
=
\begin{pmatrix}
\sum_i r_i^{(3)}(\boldsymbol{D} \tilde{\boldsymbol{\phi}})_i\\
\sum_i r_i^{(3)}(\boldsymbol{D}\boldsymbol{\phi}^{(2)})_i\\
\sum_i r_i^{(3)}(\boldsymbol{D}\boldsymbol{\phi}^{(1)})_i
\end{pmatrix}
となるので,これを解いて$\alpha_1,\alpha_2,\alpha_3$を得る.
中間変数
\begin{eqnarray}
R_{1,i} &=& \sum_{j}D_{i,j}\tilde{\boldsymbol{\phi}}_j\\
R_{2,i} &=& \sum_{j}D_{i,j}\boldsymbol{\phi}_j^{(2)}\\
R_{3,i} &=& \sum_{j}D_{i,j}\boldsymbol{\phi}_j^{(1)}
\end{eqnarray}
を導入した簡略表記は
\begin{pmatrix}
\sum_iR_{1,i}R_{1,i} &\sum_iR_{1,i}R_{2,i} &\sum_iR_{1,i}R_{3,i}\\
\sum_iR_{2,i}R_{1,i} &\sum_iR_{2,i}R_{2,i} &\sum_iR_{2,i}R_{3,i}\\
\sum_iR_{3,i}R_{1,i} &\sum_iR_{3,i}R_{2,i} &\sum_iR_{3,i}R_{3,i}
\end{pmatrix}
\begin{pmatrix}
\alpha_1\\
\alpha_2\\
\alpha_3
\end{pmatrix}
=
\begin{pmatrix}
\sum_i r_i^{(3)}R_{1,i}\\
\sum_i r_i^{(3)}R_{2,i}\\
\sum_i r_i^{(3)}R_{3,i}
\end{pmatrix}.
4.合成摂動量$\phi^{(3)}$を計算する.
\phi_i^{(3)} = \alpha_1 \tilde{\phi_i} + \alpha_2 \phi_i ^{(2)} + \alpha_3 \phi_i ^{(1)}
5.$p$を更新する.
p_i^{(3)} = p_i^{(2)} + \phi_i^{(3)}
6.$p_i^{(3)}$を用いて残差を計算し,規定値以下になっていれば反復を終了する.
mステップ目
1.残差$r_i^{(m)}$を計算する.
2.内部ソルバによって残差方程式を計算し,摂動量の近似値$\tilde{\phi_i}$を得る.
3.残差最小化係数を計算する.
$\boldsymbol{r}^{(m+1)}$の$l_2$ノルム$||\boldsymbol{r}^{(m+1)}||^2= \sum_i(\boldsymbol{r}^{(m)} - \alpha_1 \boldsymbol{D}\tilde{\boldsymbol{\phi}}-\alpha_2 \boldsymbol{D} \boldsymbol{\phi}^{(m-1)}-\alpha_3 \boldsymbol{D} \boldsymbol{\phi}^{(m-2)})_i^2$
を$\alpha_1$で微分する.
\begin{eqnarray}
\frac{\partial ||\boldsymbol{r}^{(m+1)}||^2}{\partial \alpha_1}
&=& \sum_i[-2r_i^{(m)}(\boldsymbol{D} \tilde{\boldsymbol{\phi}})_i+2\alpha_1(\boldsymbol{D} \tilde{\boldsymbol{\phi}})_i^2+2\alpha_2(\boldsymbol{D} \tilde{\boldsymbol{\phi}})_i(\boldsymbol{D}\boldsymbol{\phi}^{(m-1)})_i+2\alpha_3(\boldsymbol{D} \tilde{\boldsymbol{\phi}})_i(\boldsymbol{D}\boldsymbol{\phi}^{(m-2)})_i]\\
&=&0.
\end{eqnarray}
$\alpha_2$で微分すると
\begin{eqnarray}
\frac{\partial ||\boldsymbol{r}^{(m+1)}||^2}{\partial \alpha_2}
&=& \sum_i[-2r_i^{(m)}(\boldsymbol{D}\boldsymbol{\phi}^{(m-1)})_i+2\alpha_1(\boldsymbol{D} \tilde{\boldsymbol{\phi}})_i(\boldsymbol{D}\boldsymbol{\phi}^{(m-1)})_i+2\alpha_2(\boldsymbol{D}\boldsymbol{\phi}^{(m-1)})_i^2+2\alpha_3(\boldsymbol{D} \boldsymbol{\phi}^{(m-1)})_i(\boldsymbol{D}\boldsymbol{\phi}^{(m-2)})_i]\\
&=&0.
\end{eqnarray}
$\alpha_3$で微分すると
\begin{eqnarray}
\frac{\partial ||\boldsymbol{r}^{(m+1)}||^2}{\partial \alpha_3}
&=& \sum_i[-2r_i^{(m)}(\boldsymbol{D}\boldsymbol{\phi}^{(m-2)})_i+2\alpha_1(\boldsymbol{D} \tilde{\boldsymbol{\phi}})_i(\boldsymbol{D}\boldsymbol{\phi}^{(m-2)})_i+2\alpha_2(\boldsymbol{D}\boldsymbol{\phi}^{(m-1)})_i(\boldsymbol{D}\boldsymbol{\phi}^{(m-2)})_i+2\alpha_3(\boldsymbol{D} \boldsymbol{\phi}^{(m-2)})_i^2]\\
&=&0.
\end{eqnarray}
$\alpha_l$についての連立一次方程式は,
\begin{pmatrix}
\sum_i(\boldsymbol{D} \tilde{\boldsymbol{\phi}})_i(\boldsymbol{D} \tilde{\boldsymbol{\phi}})_i & \sum_i(\boldsymbol{D} \tilde{\boldsymbol{\phi}})_i(\boldsymbol{D}\boldsymbol{\phi}^{(m-1)})_i& \sum_i(\boldsymbol{D} \tilde{\boldsymbol{\phi}})_i(\boldsymbol{D}\boldsymbol{\phi}^{(m-2)})_i\\
\sum_i(\boldsymbol{D}\boldsymbol{\phi}^{(m-1)})_i(\boldsymbol{D} \tilde{\boldsymbol{\phi}})_i &\sum_i(\boldsymbol{D}\boldsymbol{\phi}^{(m-1)})_i(\boldsymbol{D}\boldsymbol{\phi}^{(m-1)})_i&\sum_i(\boldsymbol{D}\boldsymbol{\phi}^{(m-1)})_i(\boldsymbol{D}\boldsymbol{\phi}^{(m-2)})_i\\
\sum_i(\boldsymbol{D}\boldsymbol{\phi}^{(m-2)})_i(\boldsymbol{D} \tilde{\boldsymbol{\phi}})_i &\sum_i(\boldsymbol{D}\boldsymbol{\phi}^{(m-2)})_i(\boldsymbol{D}\boldsymbol{\phi}^{(m-1)})_i&\sum_i(\boldsymbol{D}\boldsymbol{\phi}^{(m-2)})_i(\boldsymbol{D}\boldsymbol{\phi}^{(m-2)})_i
\end{pmatrix}
\begin{pmatrix}
\alpha_1\\
\alpha_2\\
\alpha_3
\end{pmatrix}
=
\begin{pmatrix}
\sum_i r_i^{(m)}(\boldsymbol{D} \tilde{\boldsymbol{\phi}})_i\\
\sum_i r_i^{(m)}(\boldsymbol{D}\boldsymbol{\phi}^{(m-1)})_i\\
\sum_i r_i^{(m)}(\boldsymbol{D}\boldsymbol{\phi}^{(m-1)})_i
\end{pmatrix}
となるので,これを解いて$\alpha_1,\alpha_2,\alpha_3$を得る.
簡略表記は
\begin{pmatrix}
\sum_iR_{1,i}R_{1,i} &\sum_iR_{1,i}R_{2,i} &\sum_iR_{1,i}R_{3,i}\\
\sum_iR_{2,i}R_{1,i} &\sum_iR_{2,i}R_{2,i} &\sum_iR_{2,i}R_{3,i}\\
\sum_iR_{3,i}R_{1,i} &\sum_iR_{3,i}R_{2,i} &\sum_iR_{3,i}R_{3,i}
\end{pmatrix}
\begin{pmatrix}
\alpha_1\\
\alpha_2\\
\alpha_3
\end{pmatrix}
=
\begin{pmatrix}
\sum_i r_i^{(m)}R_{1,i}\\
\sum_i r_i^{(m)}R_{2,i}\\
\sum_i r_i^{(m)}R_{3,i}
\end{pmatrix},
\begin{eqnarray}
R_{1,i} &=& \sum_{j}D_{i,j}\tilde{\boldsymbol{\phi}}_j\\
R_{2,i} &=& \sum_{j}D_{i,j}\boldsymbol{\phi}_j^{(m-1)}\\
R_{3,i} &=& \sum_{j}D_{i,j}\boldsymbol{\phi}_j^{(m-2)}.
\end{eqnarray}
4.合成摂動量$\phi^{(m)}$を計算する.
\phi_i^{(m)} = \alpha_1 \tilde{\phi_i} + \alpha_2 \phi_i ^{(m-1)} + \alpha_3 \phi_i ^{(m-2)}
5.$p$を更新する.
p_i^{(m)} = p_i^{(m-1)} + \phi_i^{(m)}
6.$p_i^{(m)}$を用いて残差を計算し,規定値以下になっていれば反復を終了する.
数値実験
1次元化P問題を,SOR法およびSOR法を内部ソルバとする残差切除法で解き,収束までに要した反復回数を調査した.
離散点の個数を101とし,反復は相対残差が$10^{-9}$より小さくなるまで繰り返した.
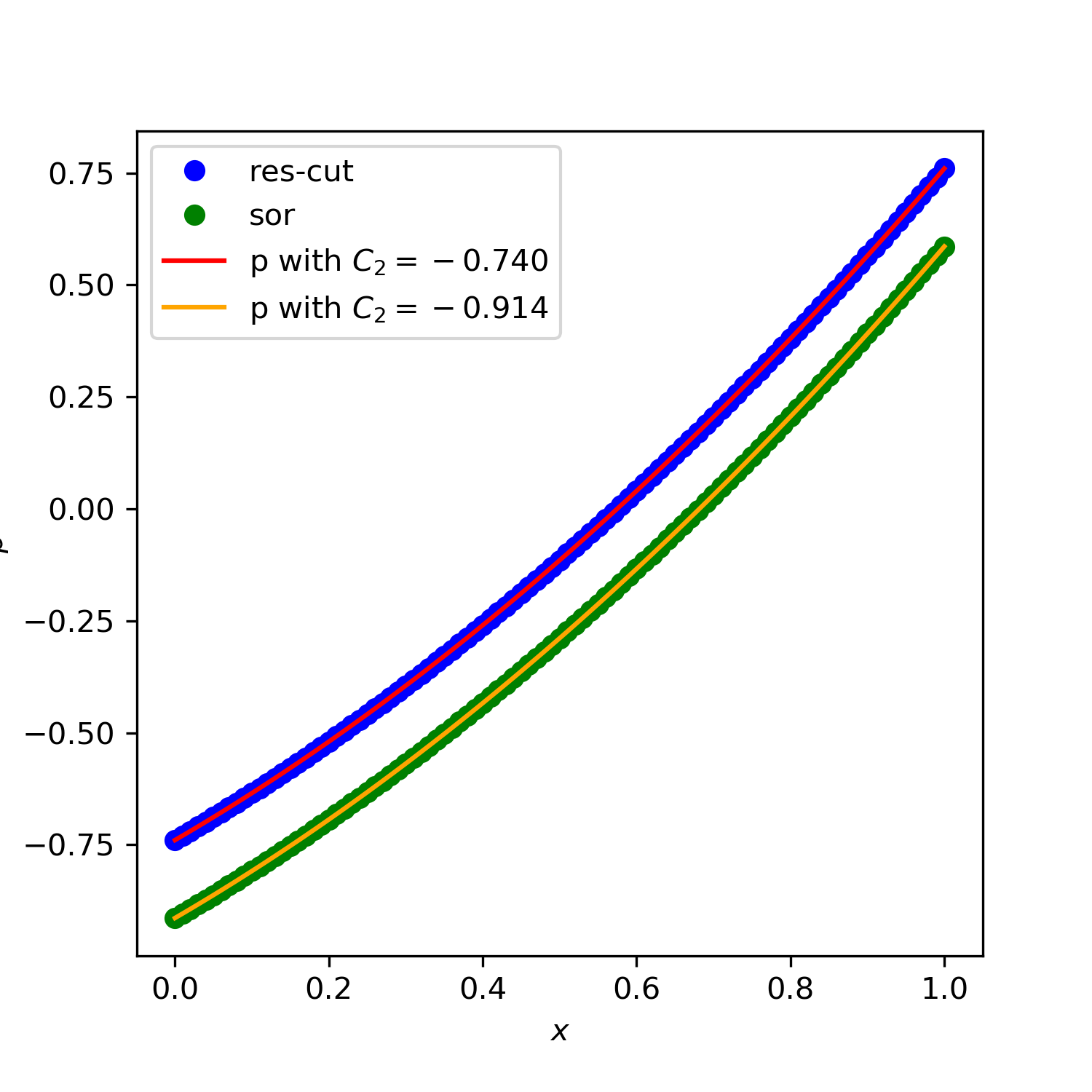
SOR法,残差切除法のどちらを用いても結果は解析解とよく一致するが,収束過程の違いにより,積分定数$C_2$の値が異なる.
SOR法
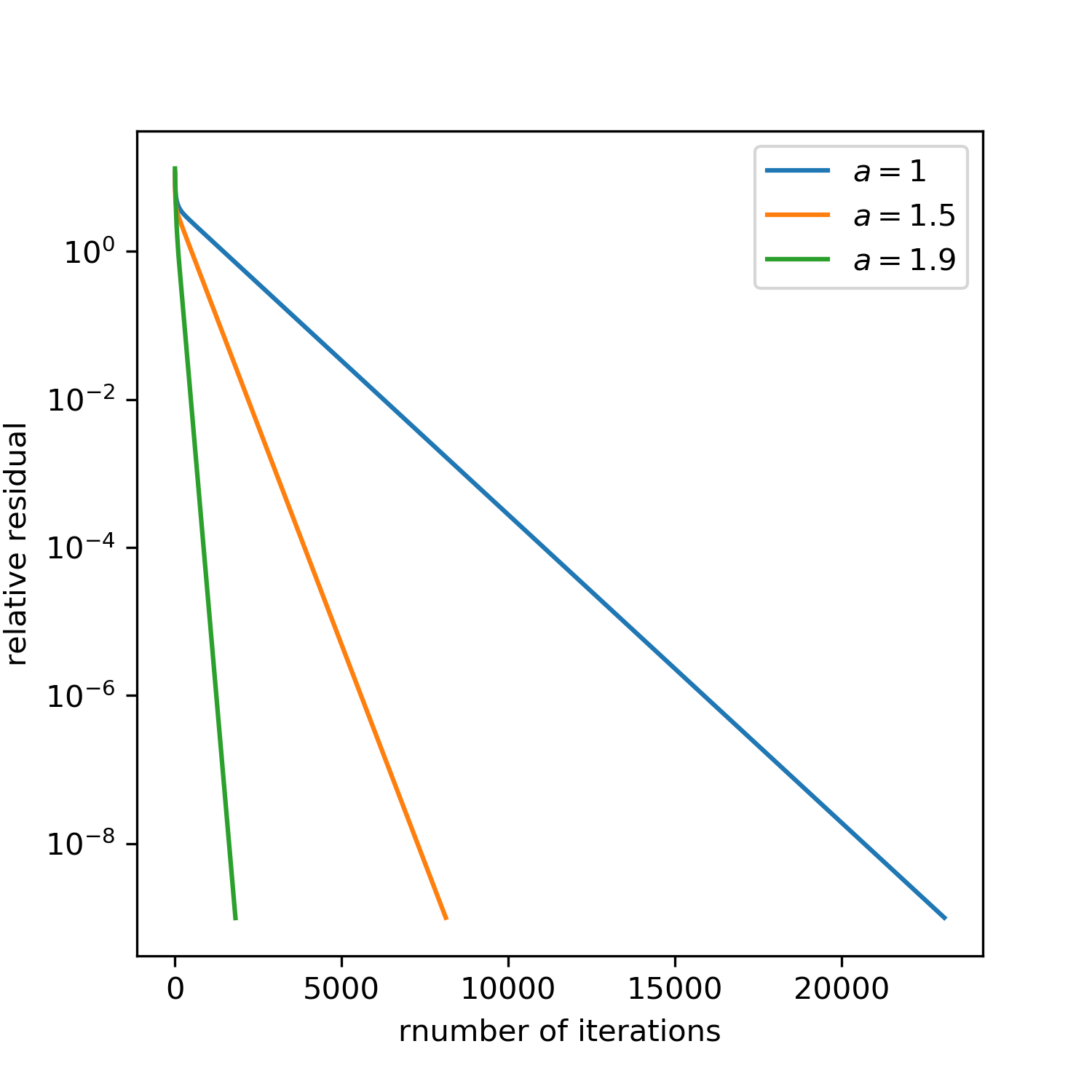
SOR法を用いる場合,加速係数$a(1\le a <2)$が任意のパラメータとなる.1次元化P問題については,加速係数が大きいほど収束が速くなった4.また,いずれの加速係数でも,相対残差は繰返し回数に比例して小さくなる.
| 加速係数$a$ | 反復回数 |
|---|---|
| 1 | 23084 |
| 1.5 | 8127 |
| 1.9 | 1816 |
| 1.99 | 690 |
残差切除法
残差切除法は,残差最小化係数の個数,内部ソルバの選択,内部ソルバで摂動量をどの程度収束させるかに任意性がある.
本記事では,残差最小化係数の個数$L=3$と固定しているので,任意のパラメータにはSOR法の加速係数$a$と繰返し回数$N_\text{ite}$がある.
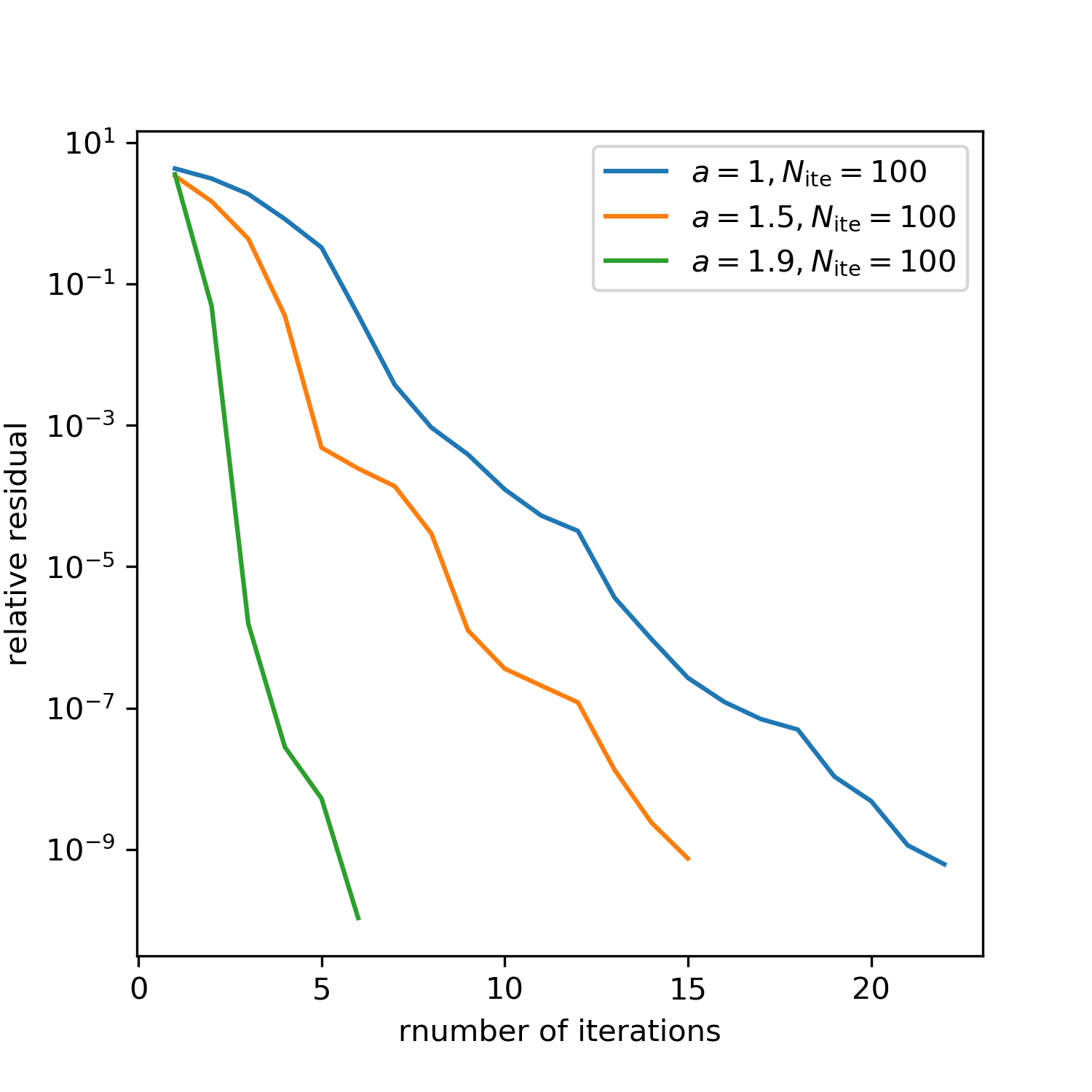
加速係数および繰返し回数の値を適当に定め,残差切除法の反復回数を調べると,下表のようになった.
| 加速係数$a$ | 内部ソルバの繰り返し回数$N_\text{ite}$ | 残差切除法の反復回数 |
|---|---|---|
| 1 | 10 | 91 |
| 50 | 35 | |
| 100 | 22 | |
| 1.5 | 10 | 79 |
| 50 | 26 | |
| 100 | 15 | |
| 1.9 | 10 | 3441 |
| 50 | 13 | |
| 100 | 6 |
残差切除法の反復回数が少なかったとしても,実際には内部ソルバが残差切除法の反復回数×$N_\text{ite}$だけ繰り返される.$N_\text{ite}=100$とした時の内部ソルバの繰返し回数をSOR法の繰返し回数と比較すると,$a=1$で約1/10,$a=1.5$で約1/5,$a=1.9$で約1/3であり,いずれの場合もSOR法より反復回数が少なくなる.内部ソルバの1反復の処理が重たい場合には,残差切除法が非常に有用であることが示唆される.残差切除法の収束性は,残差最小化係数の個数$L$によっても変化するが,残差最小化係数の個数が多くなると必要となるメモリも増加するため,問題に応じて最適な値を探す必要があろう.
残差切除法は,$N_\text{ite}$が多いほど収束が速くなり,また一部の例外があるものの,加速係数が大きいほど収束が速くなる傾向がある.これは,残差方程式をしっかり解けば正確な摂動量が得られるので,その分速く収束するという簡単な話である.したがって,内部ソルバは,規定の繰返し回数だけ反復するよりは,相対誤差や相対残差を基準とした方がよいと推察される.
反復の各ステップにおいて,内部ソルバの繰り返し後に摂動量の近似値の相対残差を計算し,全ステップの残差から最大値と最小値を抽出すると下表のようになる.相対残差の最小値が小さいほど収束が速く,また最大値が大きいと収束が遅い傾向が確認でき,この結果は上述の推察を補強する.
| 加速係数$a$ | 内部ソルバの繰り返し回数$N_\text{ite}$ | 摂動量の近似値の相対残差 |
|---|---|---|
| 1 | 10 | 0.65~0.96 |
| 50 | 0.30~0.93 | |
| 100 | 0.15~0.90 | |
| 1.5 | 10 | 0.62~1.00 |
| 50 | 0.34~0.86 | |
| 100 | 0.03~0.75 | |
| 1.9 | 10 | 0.35~1.35 |
| 50 | 0.11~1.07 | |
| 100 | 0.08~0.67 |
まとめ
Twitterで話題に上がっていた問題を残差切除法により解いた.差分法で離散化すれば普通に解ける問題なので,残差切除法の本領が発揮できる問題ではないように思うが,多次元の数値計算で全境界がノイマン条件で収束しないような場合には適用を試みる価値があると思われる.
間違いや誤解があればご指摘いただければ幸いである.
残差切除法はあまり有名ではないが,面白い方法である.その発展として一般化残差切除法も提案されているので,興味を持った方は調べてブログにまとめてもらえると,私が大変喜びます.
Markdownの互換性のNASAはなんとかならんのですかね?
-
田村, 菊地, 高橋, だ円形境界値問題の数値解法-残差切除法について : ポアソン方程式への適用, 機論B, 62巻604号(1996), pp.4076-4083. ↩ ↩2 ↩3 ↩4
-
Tamura, A., Kikuchi, K. and Takahashi, K., Residual cutting method for elliptic boundary value problems: application to Poisson’s equation, J.Comp.Phys., 137(1997) pp.247-264. ↩
-
差分法で離散化してSOR法で解けば結果はすんなり出てきます.バンザイ ↩
-
SOR法の加速係数には最適値があり,それより大きくても小さくても収束が遅くなる.本記事の結果はとても意外であり,実装過程で何らかのミスをしているのではないかと疑っている. ↩