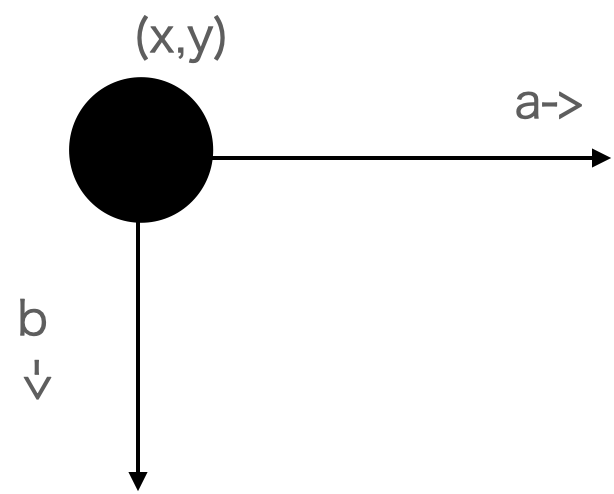で、うまく解けなかったので、
反省と備忘録を込めて記事にします。
atcoderは緑です。
(かなり備忘録の意味合いが強く僕が後で見返して理解しやすいように作成します)
累積和といもす法
厳密な話まではいもす法に関して理解するのは難しかったので、
累積和のぱっと見の考え、と上記典型90での二次元いもす法の考え方の違い(気をつけること)を記録します。
累積和
array := []int{5,4,3,2,5}
ruiseki := make([]int, len(array))
ruiseki[0] = array[0]
for i:= 1; i<len(array); i++ {
ruiseki[i] = ruiseki[i-1] +a[i]
}
// とすることで、
// 3~5などのi~jまでの配列のsumをO(1)で取れるのが強み
// あとは、累積和されたものと累積和されたものを比較して、どちらの方が多くスコアが取れる...とかを高速で行えるなど
//3 ~ 5
get := ruiseki[4] - ruiseki[2]
解説を見て噛み砕いた理解
累積和の利点を拡張するというよりも、
累積和を扱い、二次元いもす法の利点を享受する。という印象を少なくとも上記の典型90では感じました。
早速ですが、上記の問題を例に下記のものを考えます。
図のように、(x,y)の点と、水平方向ベクトルの長さと、垂直方向のベクトルの長さが分かれば、
このように、長方形を描画できそうです。(プログラミングの場合は、第4象限が+,+領域になるので、+bになりますね)
上記の問題では、
対角線上の点を得て、長方形を描画することから、(x,y)の点,a,bベクトルを得ることができます。
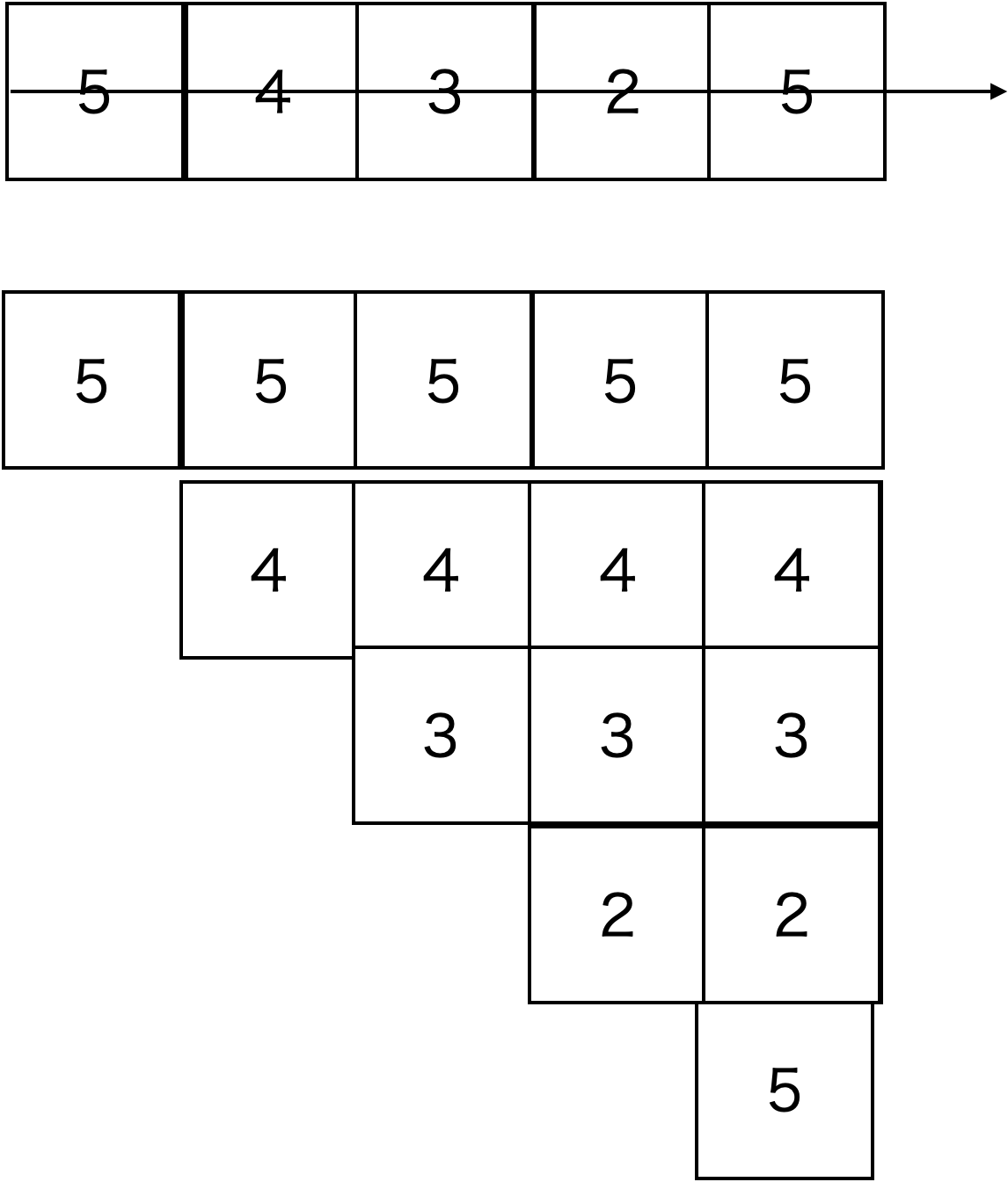
ここで、累積和をのsumを図で考えてみると
このようになっており、indexが進むごとに数字の重なりが発生します。
これを利用し、重なりを
(2の部分で二つのブロックが重なっている。)
このように表せます。
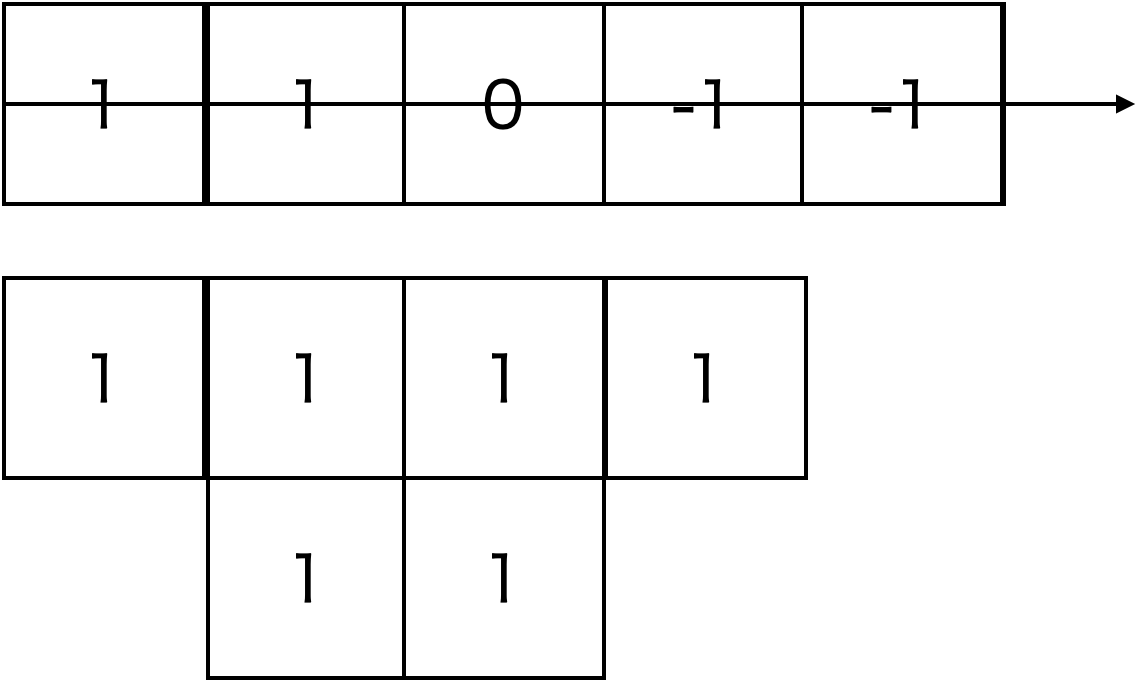
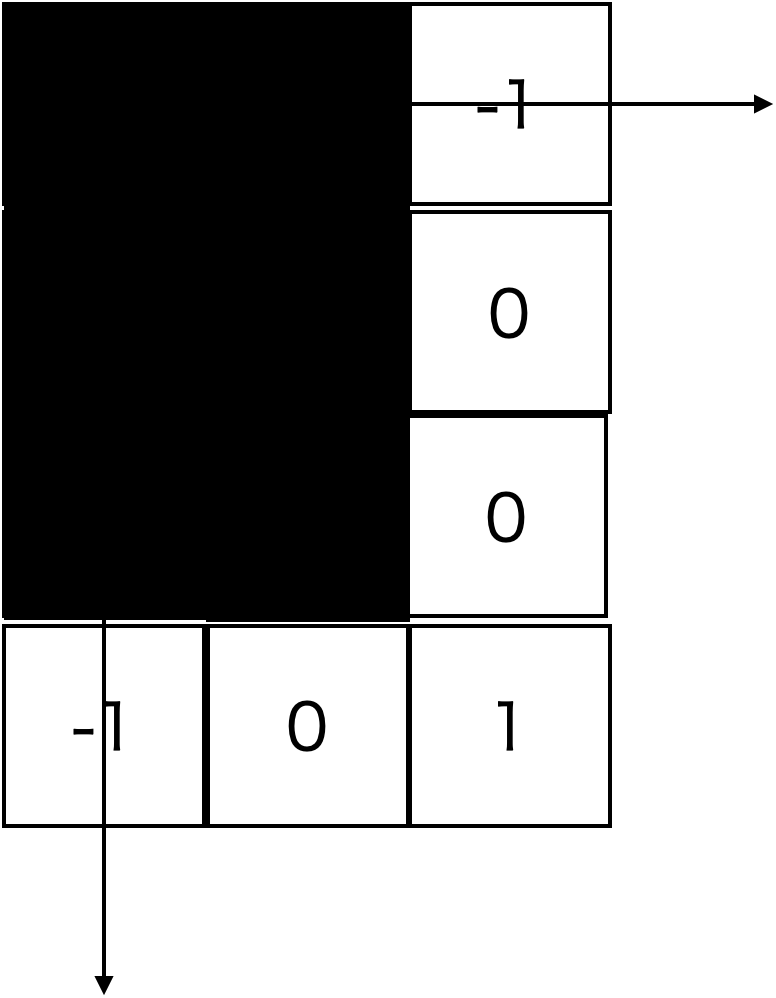
これを二次元に拡張すると
このようになります。垂直方向,水平方向のベクトルを抑えるための、-1はもちろんですが、
右下の1を考えなければいけません。
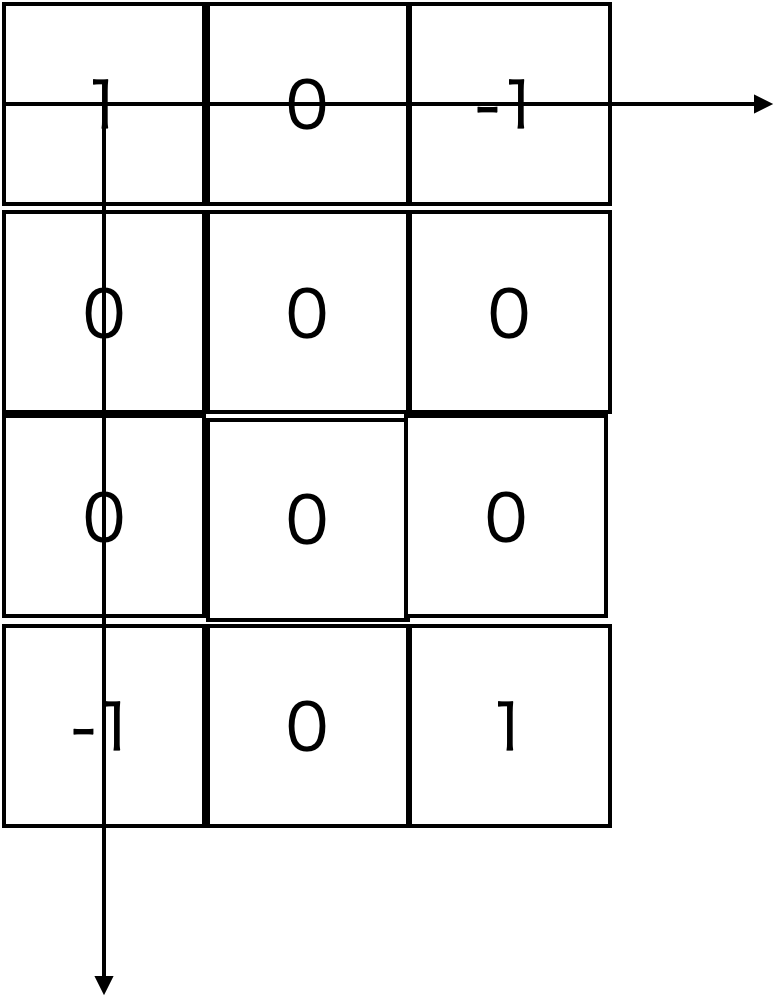
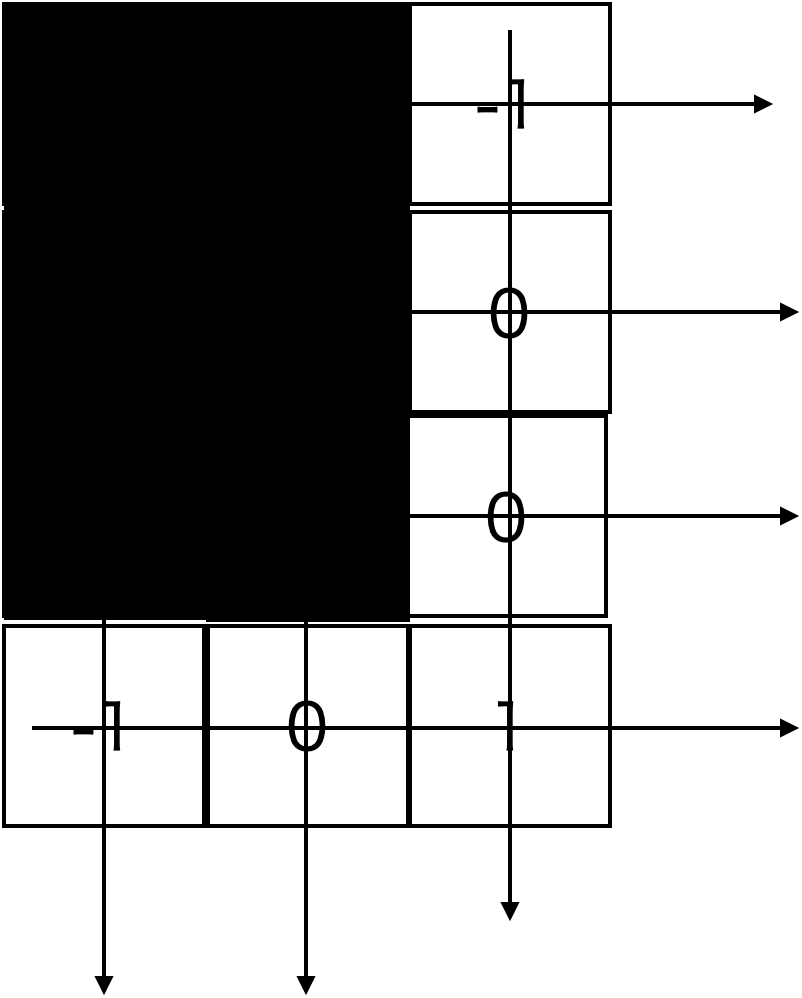
実際に、重なりを表現する場合、H,Wの二重ループになり
このようになります
その場合、垂直方向、水平方向を相殺するための1を配置しなければ、-1が永久に作用し続けます。
このように考えることで、
二次元上に、N個の長方形が存在していても、その重なりを、O(N+HW)で計算できます。