制約付き最小化問題をscipy.optimize.minimizeで解く
scipyにはminimizeという、与えた目的関数値を賢く最小化してくれる関数が入っています。
主に線形計画法なんかで使われたりすることが多いです。
最小化にも
- 取りうる値が連続 OR 離散
- 関数が線形 OR 非線形
- 変数の次元が1つ OR 複数
- 制約条件のあり OR なし
などのパターンがあり、それらに応じ最適なアルゴリズムを選択する必要があります。
これらのアルゴリズムは後述するようにmethodオプションに文字列で渡すことで指定できます。
今回は制約付き非線形最適化問題を扱う場合の話です。
制約条件付き非線形最小化問題を扱うアルゴリズムはCOBYLAとSLSQPの2つです。
呼び出しは以下のようにします。
from scipy.optimize import minimize
result = minimize(func, x0=x, constraints=cons, method="SLSQP")
ここでfuncは目的関数への参照、x0は解探索を開始する出発点の座標です。
またconstraintsが制約条件を与えるオプションになっていて、内容的には以下の様なディクショナリを渡します。
typeは制約条件が等号(eq)か不等号(ineq)かを表すものです。
cons = (
{'type': 'ineq', 'fun': cons(x)},
{'type': 'eq', lambda: x: x ** 2 - 2 * x + 1}
)
制約条件constraintsを与える際の疑問点
しかしこのconstraintsオプションの使い方がイマイチわかりませんでした。
具体的に言うと
-
eq/ineqは何と等しい/等しくないことを表しているのか?? -
ineqの不等号はどっちに向いてるのか??
という疑問がありました。
結論
この点は**公式リファレンスにちゃんと書かれていました。**
Equality constraint means that the constraint function result is to be zero whereas inequality means that it is to be non-negative. Note that COBYLA only supports inequality constraints.
(訳) 等号制約(
eqを指定した場合)は与えた制約条件式の値が0に等しくなることを意味し、一方で不等号制約(ineqを指定した場合)は式の値が非負となることを意味します。なおCOBYLAは不等号制約のみサポートしていることに注意してください。
つまり
x \leq -1
のような不等号制約条件の場合、一度左辺へ式を寄せてしまって
g(x) = x + 1
としたうえで
g(x) \leq 0
であると考えます。
この$g(x)$を'type': 'ineq'で渡すことで**「$g(x)$は非負だよ」という条件になり、当初の目的を達成します。**
以上から
-
eq/ineqはそれぞれ0と等しい及び**0以上(非負)**であることを表す -
ineqの不等号は**常に「$(与えた式) \geq 0$」**となる
あまり日本語への翻訳情報がなかったのでメモ書きしておきました。
プログラムを組んでみる
それでは実際にプログラムを組んでみます。
今回は説明の、あえてscipyを使うまでもないような二次関数の最小化をやってみます。
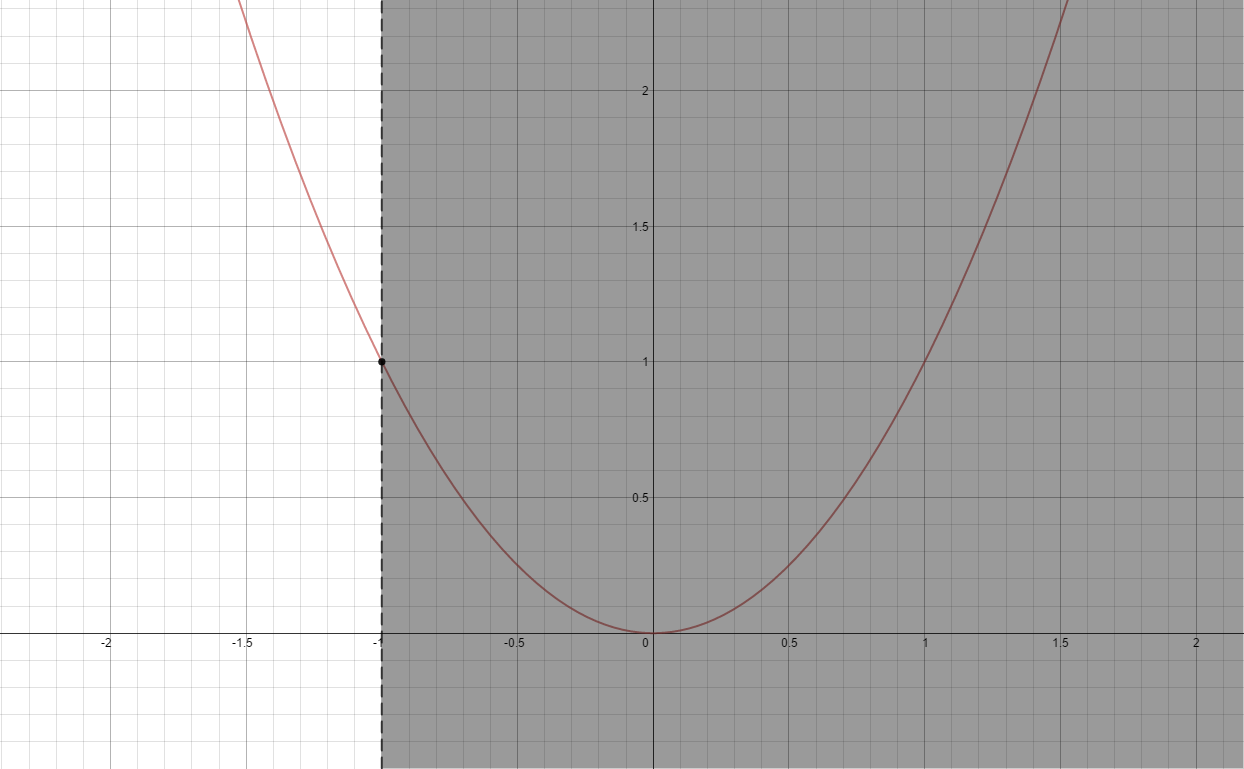
\underset{x}{minimize} \: f(x) = x^2\\
s.t. x \leq -1
グラフに表すとこんな感じで、$(x,y) = (-1, 1)$が解となるはずです。
まずは問題における目的関数$f(x)$です。
def func(x):
return x**2
これは簡単ですね。
次に制約条件ですが、こちらも関数にしてあげます。
簡単な式であればlabmdaで与えることもできますが、今回はあえて前者の方式にしますので
def cons(x):
return -(x + 1)
のようにして、最終的に以下の通りとなります。
from scipy.optimize import minimize
# 目的関数
def func(x):
return x ** 2
# 制約条件式
def cons(x):
return -(x + 1)
# 制約条件式が非負となるようにする
cons = (
{'type': 'ineq', 'fun': cons}
)
x = -10 # 初期値は適当
result = minimize(func, x0=x, constraints=cons, method="SLSQP")
print(result)
結果で(x, fun) = (-1,1)が得られれば成功です。
> python constraints_sample.py
njev: 2
status: 0
fun: array([ 1.])
x: array([-1.])
nit: 2
success: True
message: 'Optimization terminated successfully.'
jac: array([-1.99999999, 0. ])
nfev: 6
もちろん次元が増えた場合も、numpy.arrayなどで扱うことができます。