この記事はABEJA Advent Calendar 2020の14日目です。
私はF1レースが大好きでもう20年以上も見続けているのですが、F1に関わるデータ分析をしてみたいと思いKaggleを眺めていたところ、chrolss氏が面白い問題「Formula 1: What makes a good race?」を紹介していました。
問題は「F1のレースデータから、そのレースがどれくらい面白かったかのユーザ評価を予測する」というもので、私も今回この問題に取り組んでみました。
(余談ですが、来年はF2でも今年大活躍した角田選手のF1アルファタウリチームへのの昇格が確実視されており、楽しみです![]() !)
!)
データ
F1のレースデータと、各レースに対するユーザ評価データは以下の通り取得しました。
-
F1レースデータ:Chris Gさんが公開してくれているF1 Race Data
- 1950〜2017年までのレースデータ(予選・決勝順位、レース中のラップタイム、ピットストップ、リタイア原因などの詳細情報)
-
ユーザ評価データ:racefans.netで公開されているユーザによる評価データ
- 毎レース終了後、集計されるユーザー投票の平均値(0:非常につまらなかった〜10:非常に面白かった)
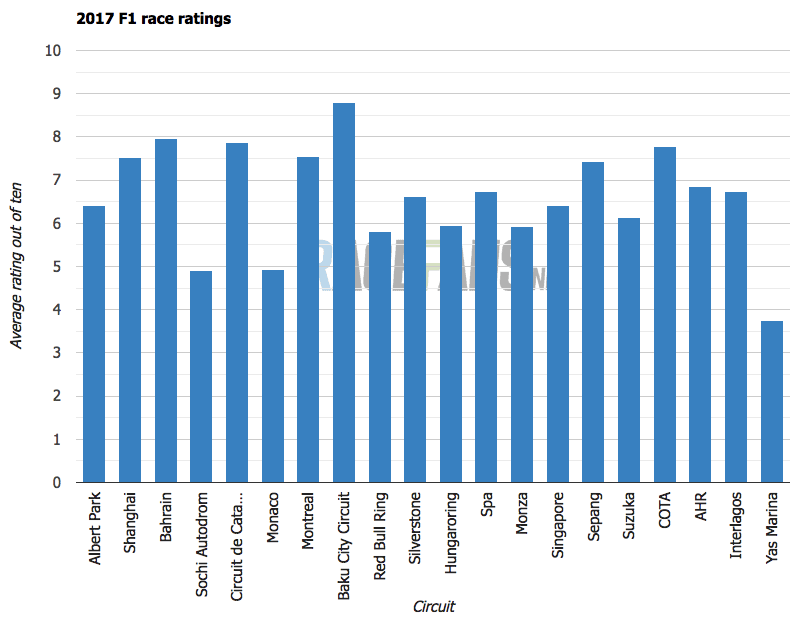
- 2017シーズンのユーザ評価例(https://www.racefans.net/2017/12/26/2017-ended-with-second-worst-race-of-last-ten-years/ より引用)
特徴量
特徴量として、以下の3つを定義してみました。
特徴量①:アクシデント率
クラッシュやトップ周回中のドライバーにパンクが起こったりすると、レースが荒れて結果としてユーザ評価が高まることが考えられます。
今回のレースデータには、各ドライバーがどのようにレース終えたかを示すステータスが定義されており、その中でもアクシデント関連として以下のようなものが定義されています。

そこで、あるレースでレースに出走したドライバーの内、どれくらいがアクシデントでレースを終えたかを**アクシデント率(accident_rate)**として以下のように定義しました。
アクシデント率 = \frac{上記の表に含まれる理由でレースを終えたドライバー数}{レースに出走したドライバー数}
特徴量②:年間累積勝利数
同じドライバーが勝ち過ぎると、そのドライバーの熱烈なファンでも無い限りは、レースの展開に意外性がなくなり、ユーザ評価は下がると考えられます(例:2004年はMichael Schmacherが18レース中13勝したので、あんまり面白くありませんでした)。
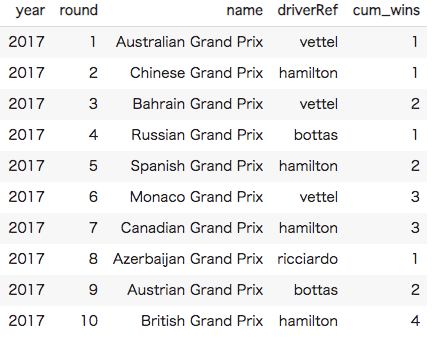
そこでレースに優勝したドライバー年間の**累積勝利数(cum_wins)**を求めてみました。以下の2017年シーズンの例だと、10戦目時点でLewis Hamiltonが4勝しています。
特徴量③:予選から決勝への合計順位変化
ドライバーの予選順位から、最終的な決勝での順位が大きく異なれば異なるほど、オーバーテイクが発生したり、順位の入れ替わりが激しいレースと言えるので、ユーザ評価が上がる可能性が考えられます。
そこで各ドライバーの予選順位と決勝順位の差分の絶対値を考え、それを全ドライバー分について足し合わせた**合計順位変化(delta_pos)**を以下のように求めました。なおリタイアした場合は、差分は0として取り扱います。
合計順位変化 = \sum_{i=0}^N |予選順位(ドライバー_i) - 決勝順位(ドライバー_i)|
定義した特徴量とユーザ評価の関係
定義した特徴量とユーザ評価(rating)の関係を以下のとおり調べてみました。
| 特徴量 | ユーザ評価との関係 | 相関係数 |
|---|---|---|
| アクシデント率 | 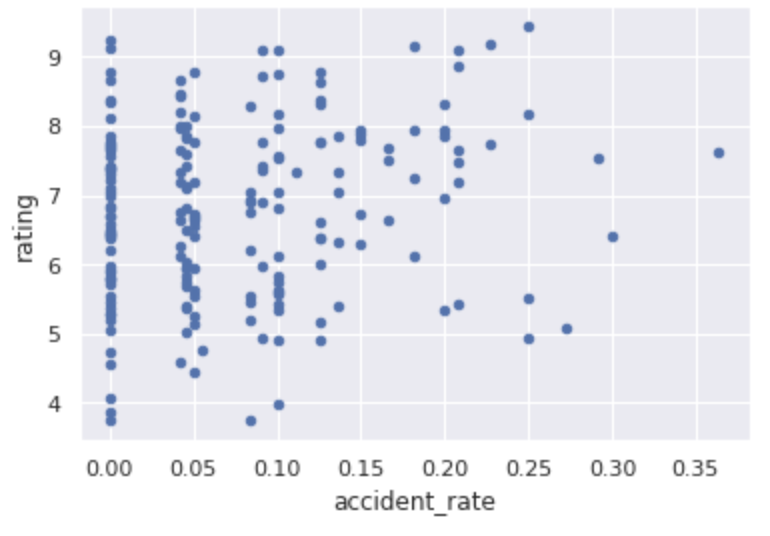 |
 |
| 累計年間勝利数 | 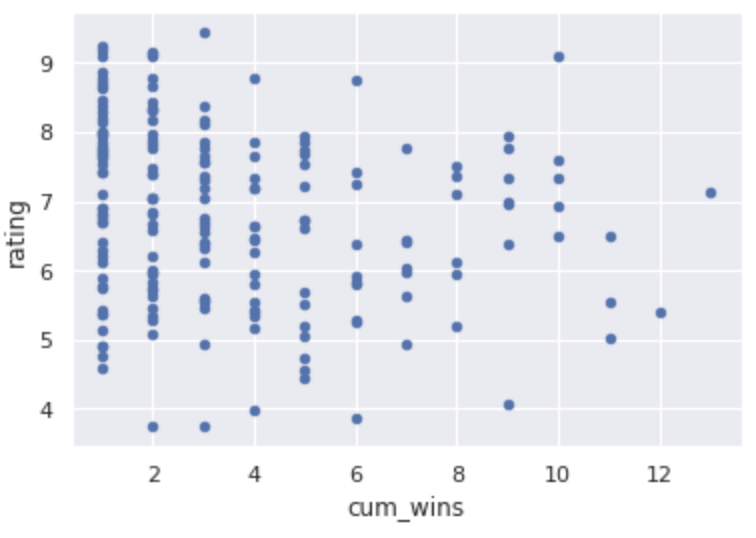 |
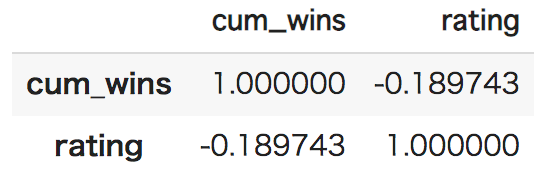 |
| 合計順位変化 | 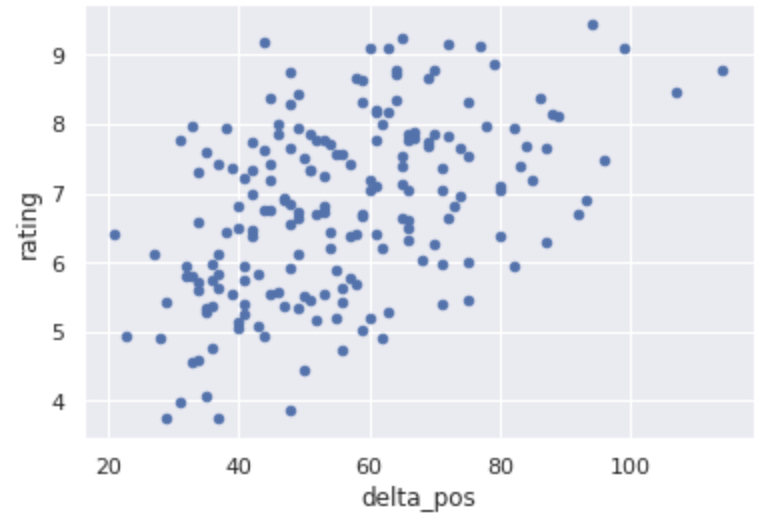 |
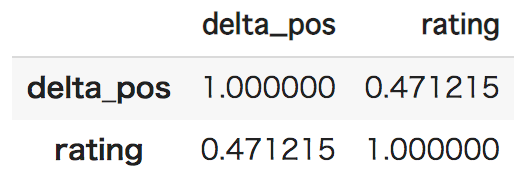
|
アクシデント率と累計年間勝利数は、ユーザ評価との相関があまり高くなさそうです😓。
ただし累計年間勝利数は、意図したとおり負の相関(累計年間勝利数が上がるほど、ユーザ評価が下がる)となっています。
また合計順位変化は、全体的には右肩上がりの正の相関分布となっており、相関係数も0.47と比較的高めになっており、有望そうです。
実験
実験設定
2008年〜2017年シーズンのデータをランダムに分割して、7割を訓練データ、3割をテストデータとして、xgboostを使ってMSEを最小化するように学習しました。
以下の4つのケースを比較してみました。
- ①ベースライン:学習データのユーザ評価平均(6.766)を予測値とする
- ②proposed: 今回定義した特徴量で学習・予測を行う
-
③chrolss: chrolss氏が「Formula 1: What makes a good race?」で用いていた特徴量で学習・予測を行う
- 追い抜きの数、リタイアの数、決勝順位top5ドライバーのレース中順位の分散
- ④chrolss + proposed: chrolss氏+今回定義した特徴量で学習・予測を行う
結果
テストデータに対する予測と実測値のMean Absolute Errorを上の4つのケースに対して求めてみたのが以下になります。
残念ながら今回定義した特徴量(②)は、ベースライン(①)よりは若干良かったものの、chrolss氏の特徴量(③)には敵いませんでした。ただ、chrolss氏の特徴量と今回のものを両方使うと(④)、若干エラーが改善しました!
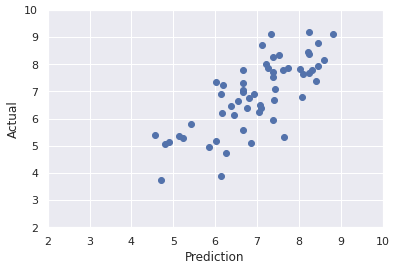
④の場合の、最終的なユーザ評価の予測値(X軸)と実測値(Y軸)の関係は以下のとおりになります。結構当たっているように見えます!
感想
結果として今回定義した特徴量は単独ではあまり良い予測に寄与することはできませんでしたが、自分の好きなデータを眺めながら色々と特徴量を考えてみるのは楽しかったです。
また今回は時間の関係でできませんでしたが、各ドライバーの順位データの時系列データをLSTMに入れて、Deep Learning的なアプローチも試してみるのも面白そうだと思いました。
ツッコミどころあれば、ぜひよろしくお願いします。