この記事はJubatus Advent Calendar 20日目の記事です.
本日は、昨日の記事の続きでJubatus分類器の中身について解説します!
非線形分類器 : k近傍法
jubaclassifierでは、非線形分類器としてk近傍法を用意しています。
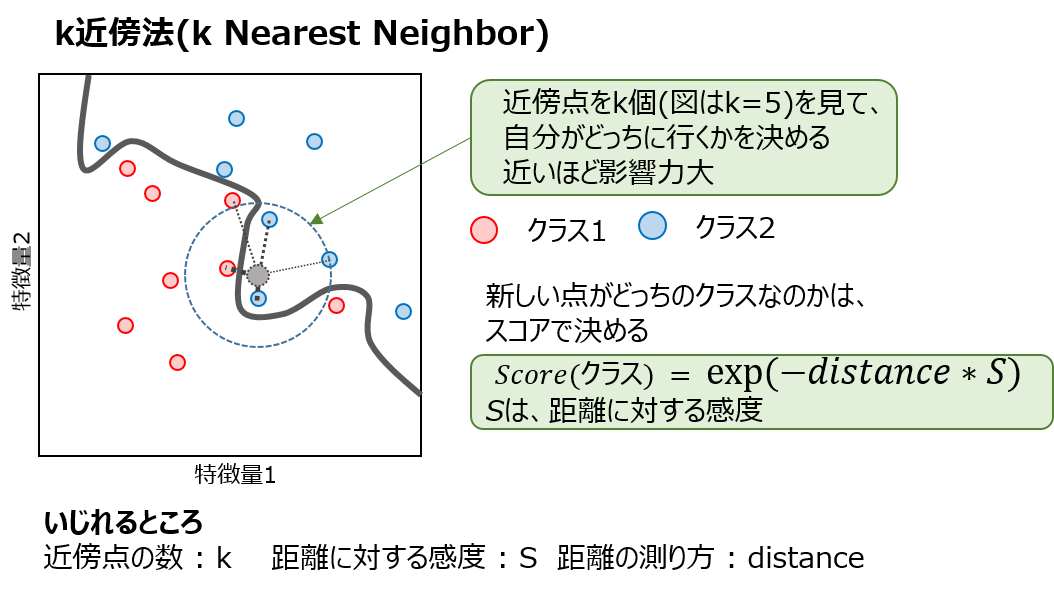
k近傍法は、新しくデータが入ってきたときに、下記の要領で自分のクラスを決定します
- データの近傍に存在するデータをk個探索する
- 得られたk個のデータについてラベルごとにスコアを求める
- スコアの大きいほうが自分のクラスとなる
図示すると、次のようなイメージです
図でも書いてあるとおり、**距離の測り方(distance)**を、いろいろいじることができます。
Jubatusには
-
厳密な近傍計算を行う
euclidean,cosine -
ハッシュに基づき近傍計算を行う
euclid_lsh,lsh,minhashを用意をしているので、順に説明していきます
厳密な近傍計算
- 設定 : i番目の点とj番目の点の距離$d(x_i,x_j)$を求める
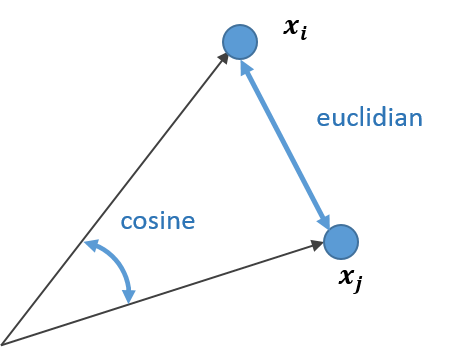
euclidian
単純なユークリッド距離で差を計算します
\begin{eqnarray}
d(\mathbf{x_i},\mathbf{x_j})=||\mathbf{x_i}-\mathbf{x_j}||
\end{eqnarray}
cosine
原点からの角度(厳密には$\cos{\theta}$ )によって類似度を出します。ベクトルの大きさは関係ありません。
\begin{eqnarray}
d(\mathbf{x_i},\mathbf{x_j})=\frac{\mathbf{x_i}\cdot\mathbf{x_j}}{|\mathbf{x_i}||\mathbf{x_j}|}
\end{eqnarray}
ハッシュに基づく近傍計算
Jubatusでは、高速にアルゴリズムを動作させるため、ハッシュ関数を用いて計算を行うことがあります。
- i番目の点とj番目の点の距離$d(x_i,x_j)$を求める
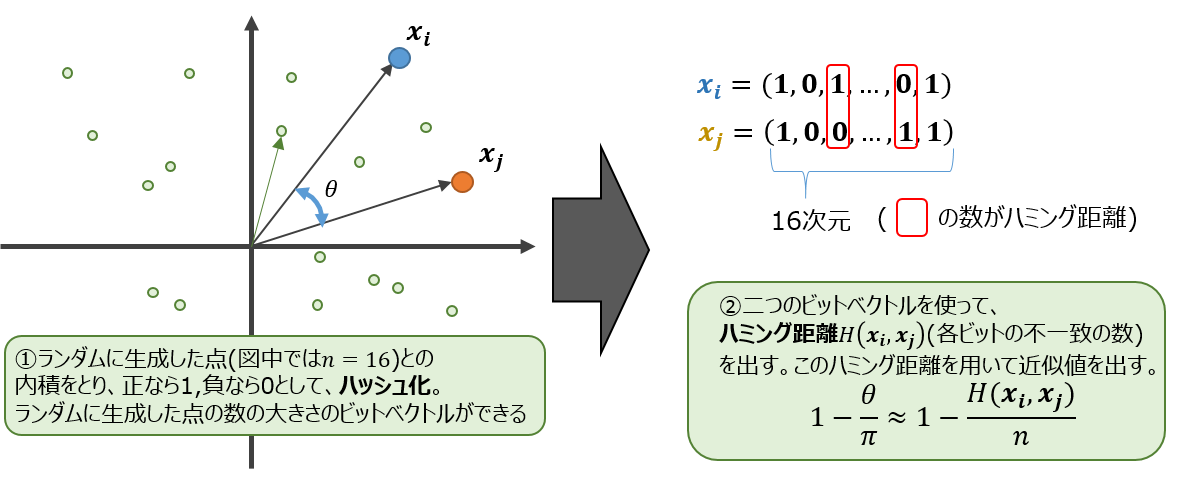
LSH
Local Sensitivity Hash の略です。
ランダムベクトルを用意してハッシュを作り、二つのベクトルの近似的なコサイン類似度を求める方法です。
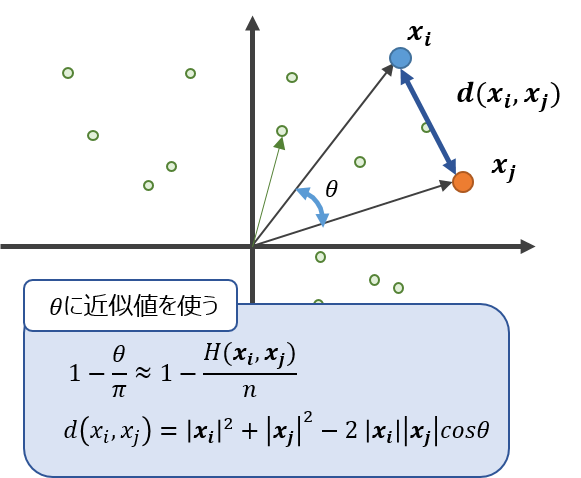
ハミング距離によって近似した$\theta$をつかい、コサイン類似度とします。
なお、k近傍法でほしいのはコサイン類似度の順序です。$1-\frac{\theta}{\pi}$ も $\cos\theta$ もどちらも($0<\theta<\pi$)において単調減少関数なので、Jubatusでは計算量削減の観点から、わざわざ$\cos\theta$を計算することなく, $1-\frac{\theta}{\pi}$ の値をコサイン類似度として採用しています。
Euclid LSH
LSHで近似的に求めた$\theta$を使って、二つのベクトルの距離を求める方法です。
MinHash
Min-Wise Independent Permutationの略称で、類似度指標であるJaccard係数を、ハッシュを用いて近似的に求める手法です。
(※後日加筆するかもです。。。)
パラメータごとの挙動の違い
ここまで、線形分類器と非線形分類器のアルゴリズムを紹介してきました。
お分かりだと思いますが、それぞれの分類器では、自分たちで設定できるパラメータが存在します。
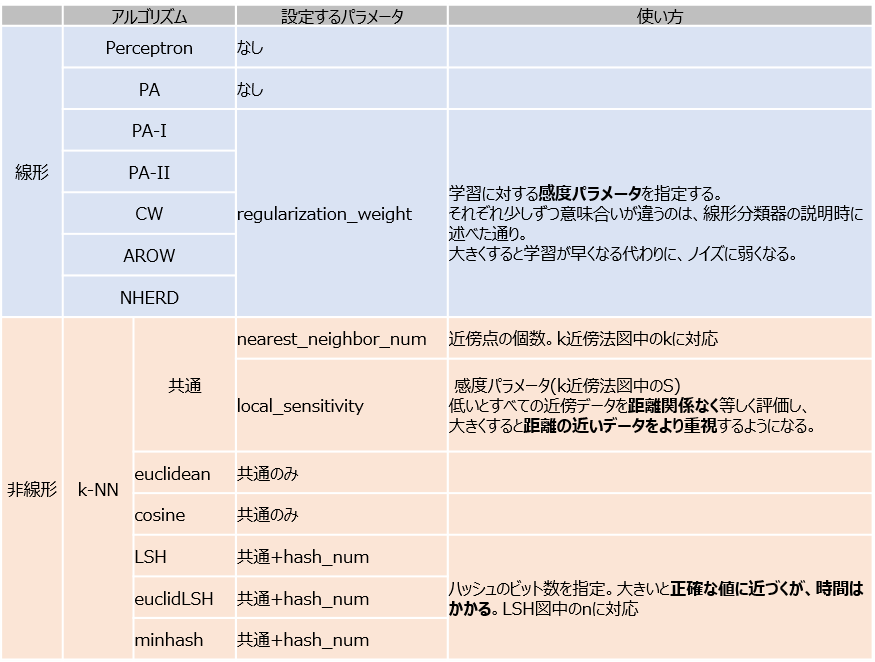
下の表は、jubaclassifierにおいて設定できるパラメータたちです。
先日、@shiodatさんがアルゴリズムごとの挙動の違いについては説明してくれたので、私はパラメータによるの挙動の違いについて少し見てみようかなと思います
regularization_weight
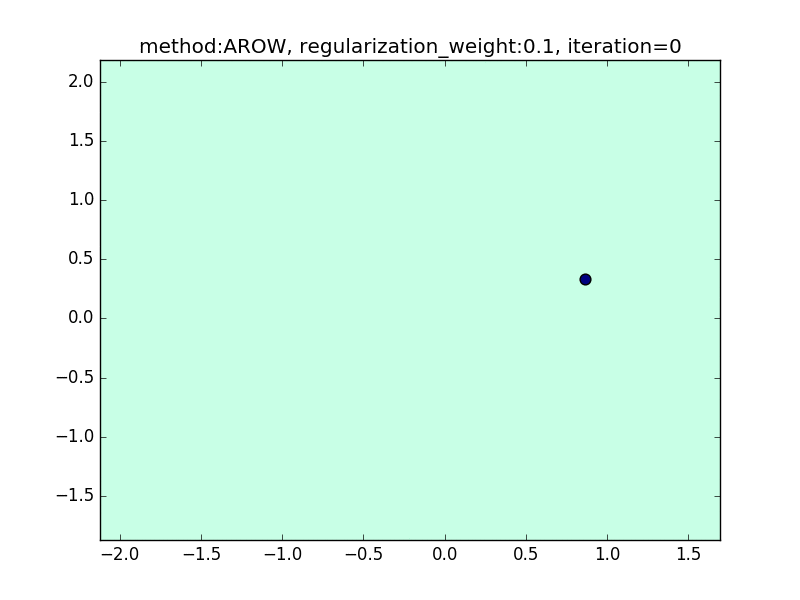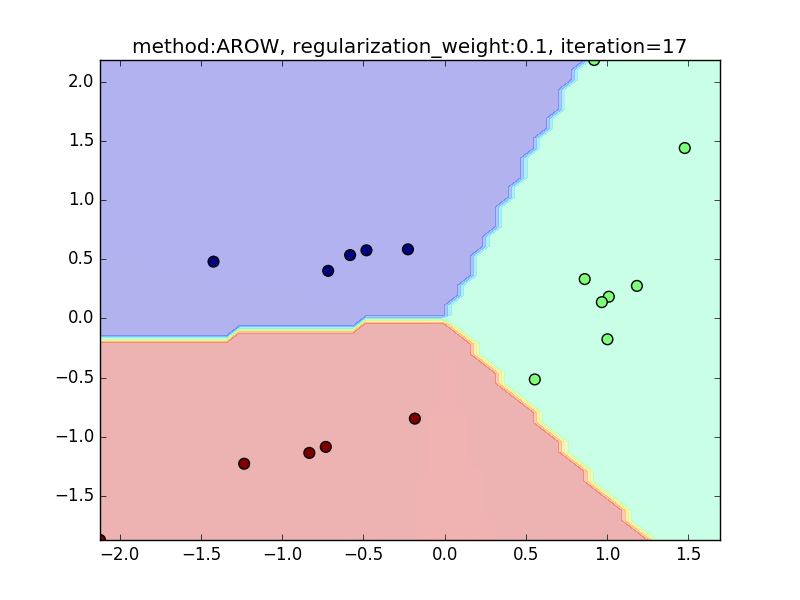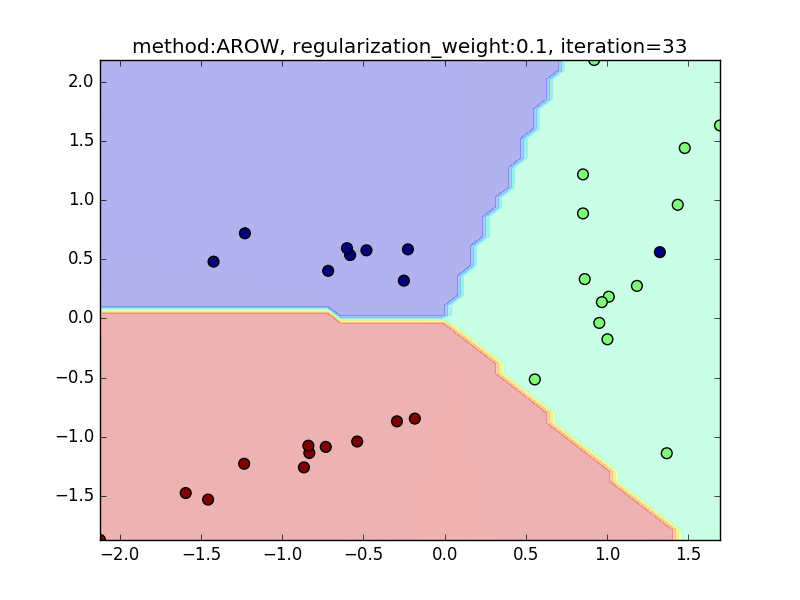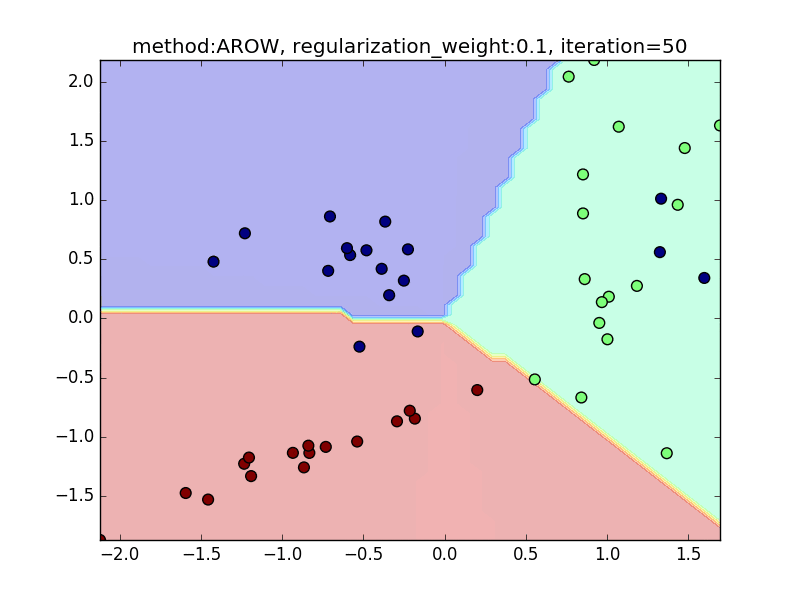
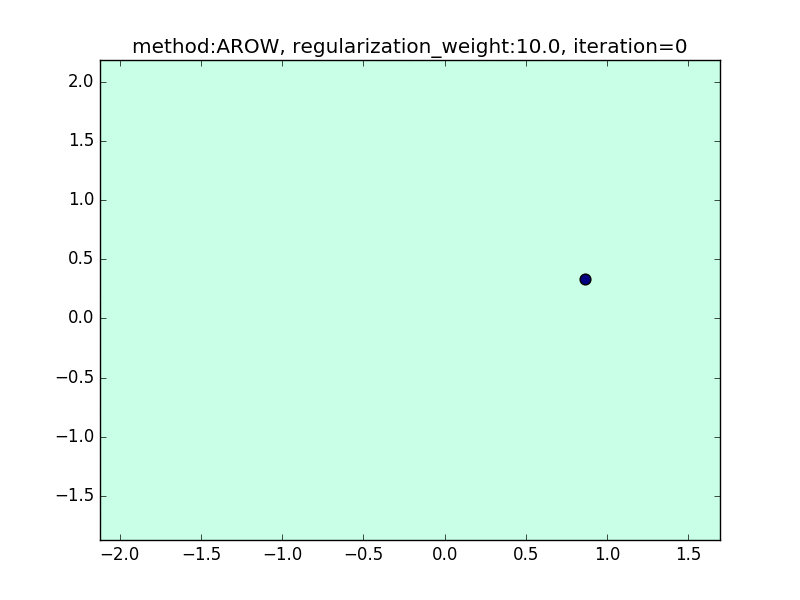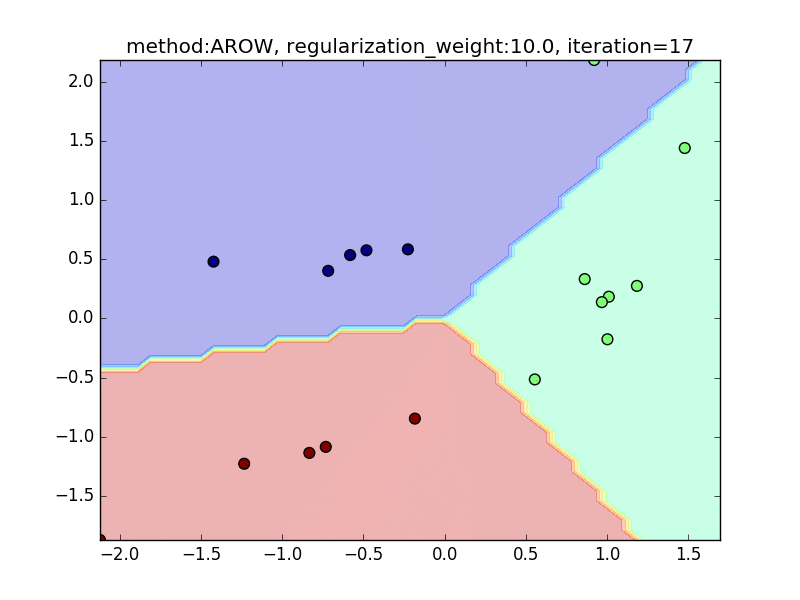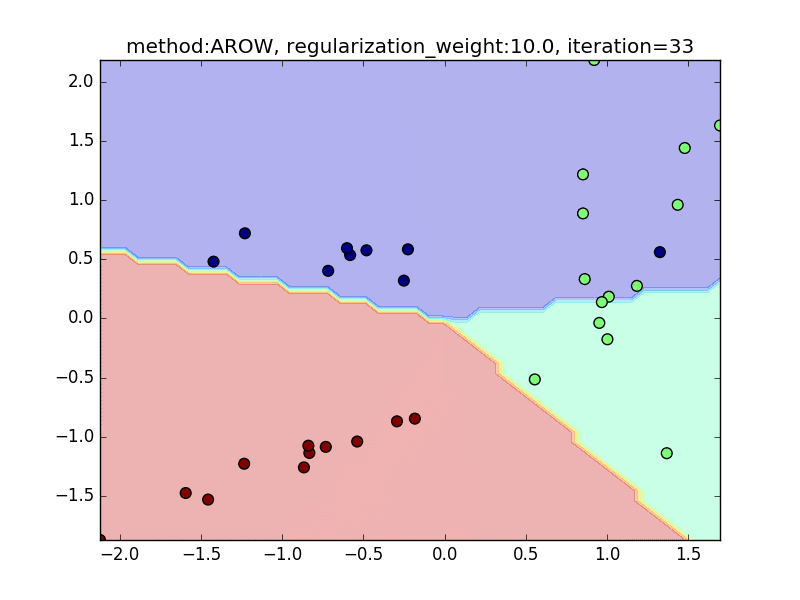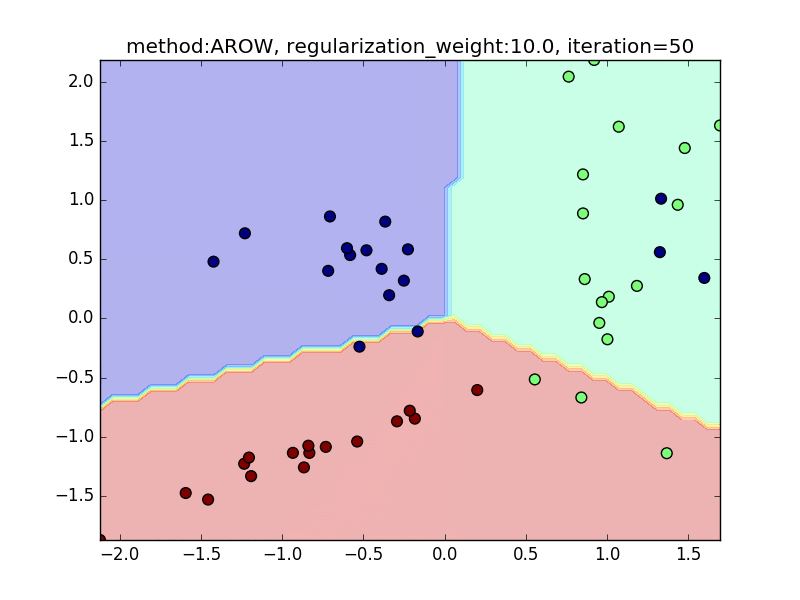
今回は、AROWを例にとり、regularization_weightによる違いを見てみたいと思います。
特に、iteration=40 近辺のバタつきに注目してみてください。
regularization_weightが大きいとばたつきが大きくなることがわかると思います。
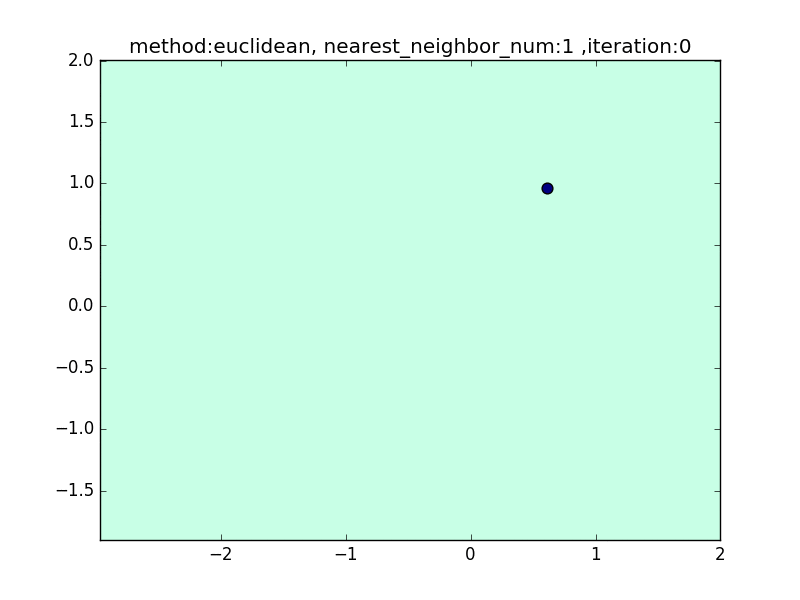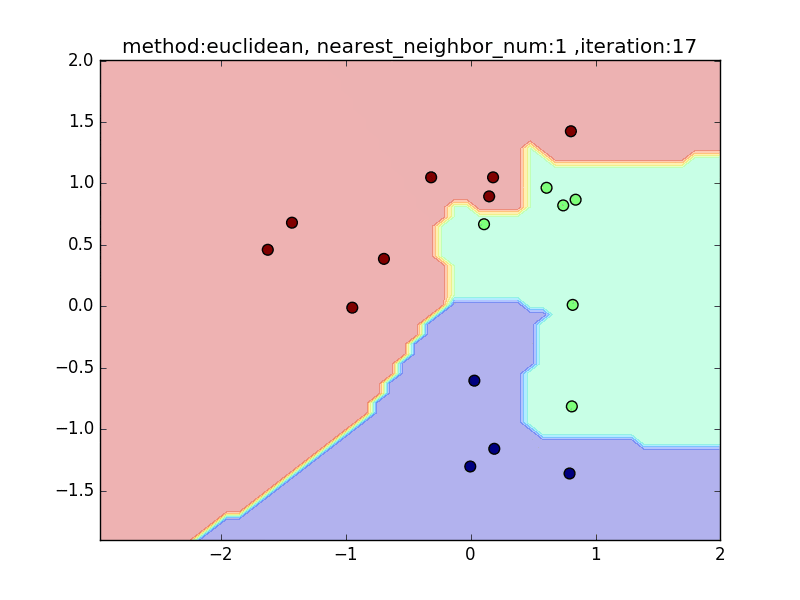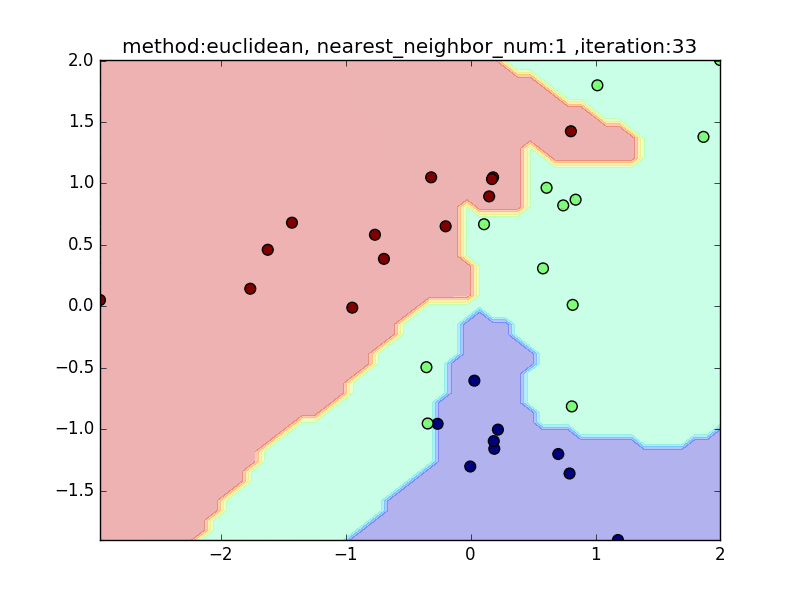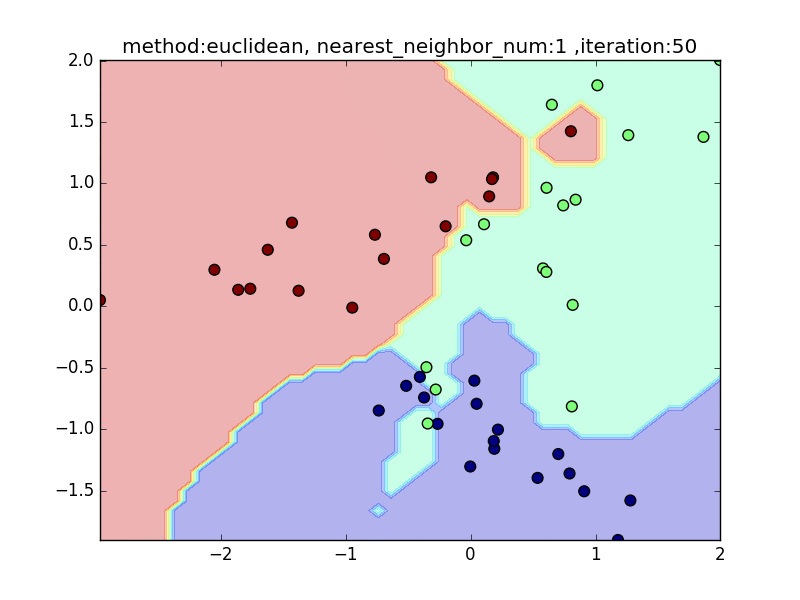
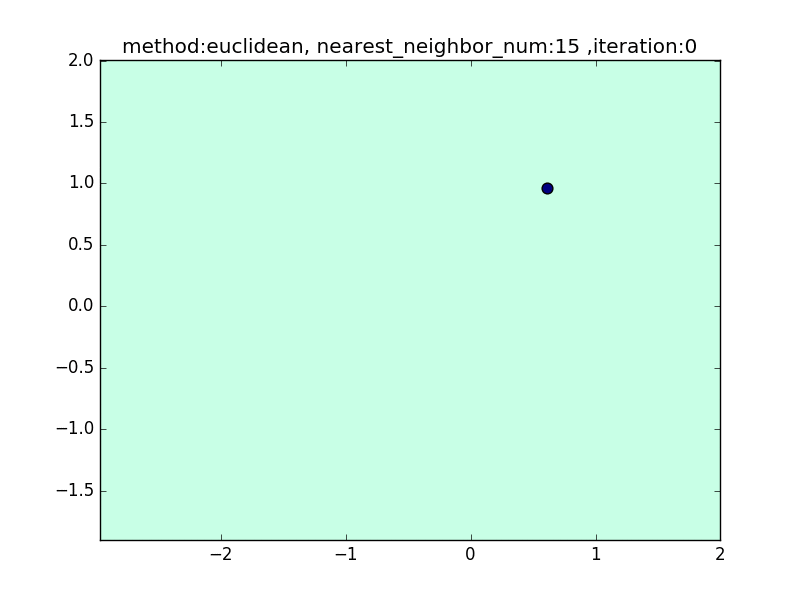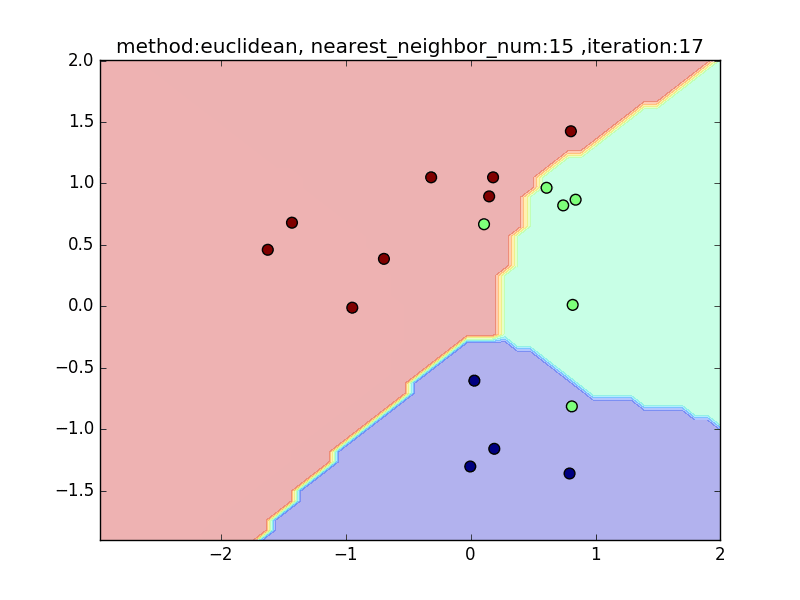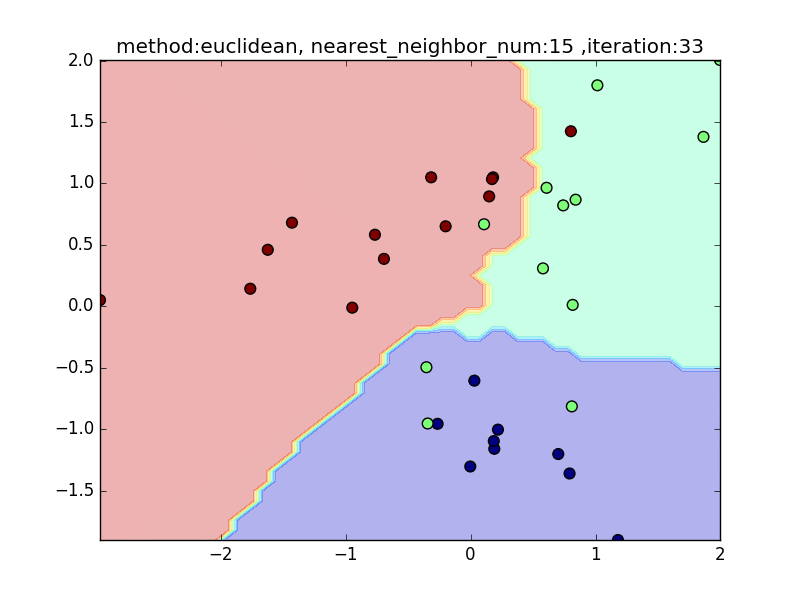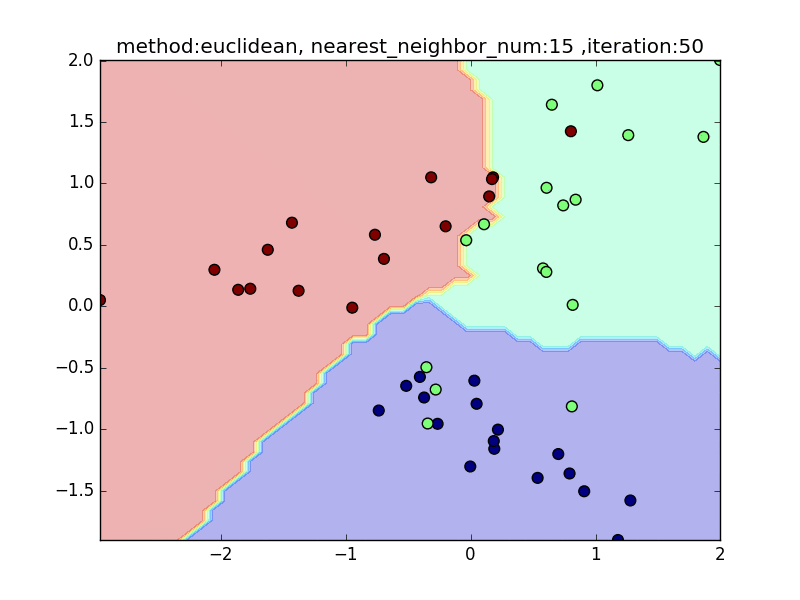
nearest_neighbor_num
(distance : euclidean, local_sensitivity = 1.0)
近傍点の数が少ないと、1点の周りに特化した境界面になります。そのため、きちんとすべてを分類できますが、過学習を起こしがちになります。
近傍点の数を増やしていくと、周りを見ながら近傍点を設定するので、境界面はそこまでぐにゃっと曲がることはありません。その反面で、少し分類しきれない点も出てきます
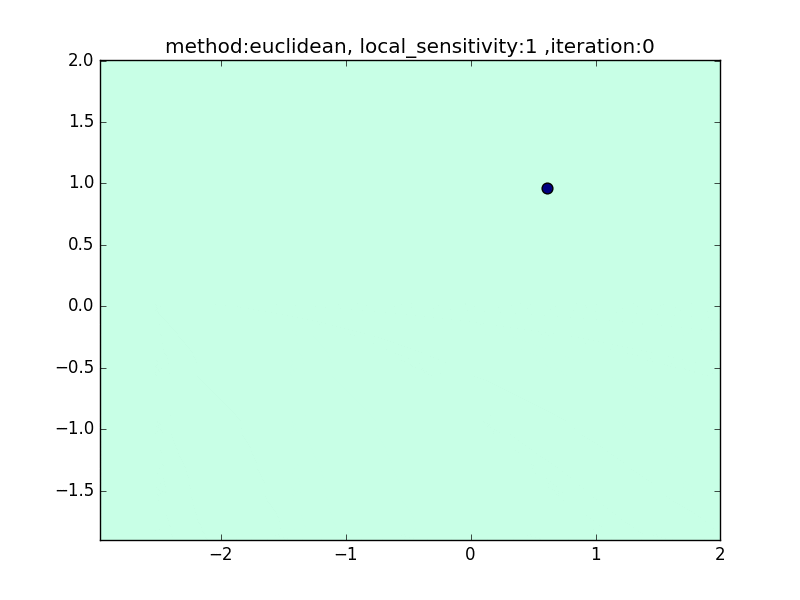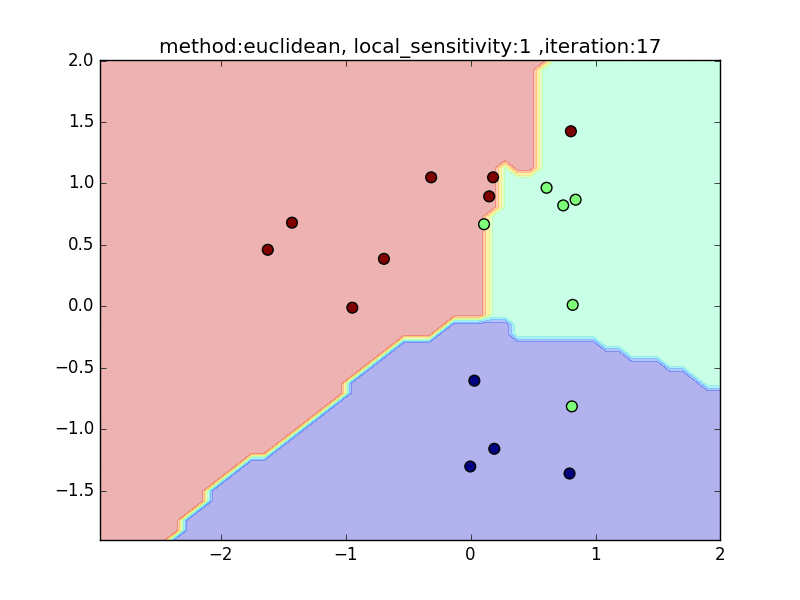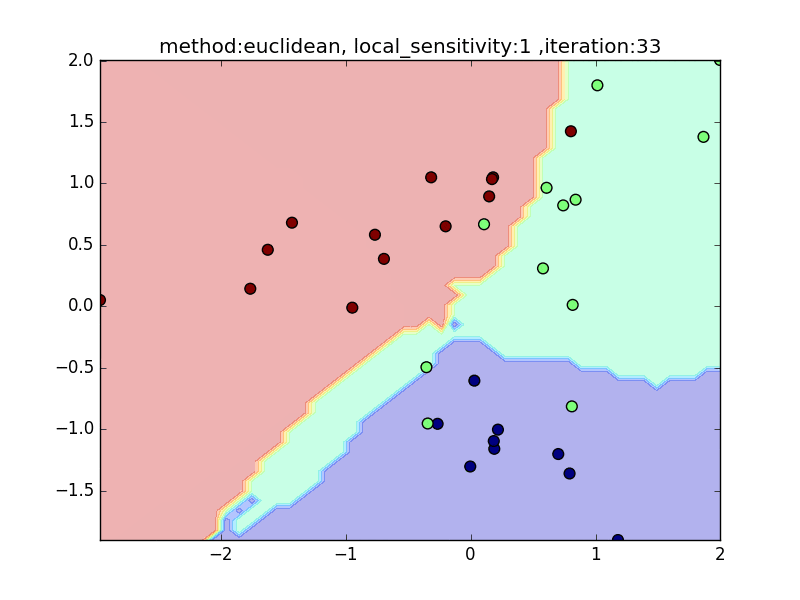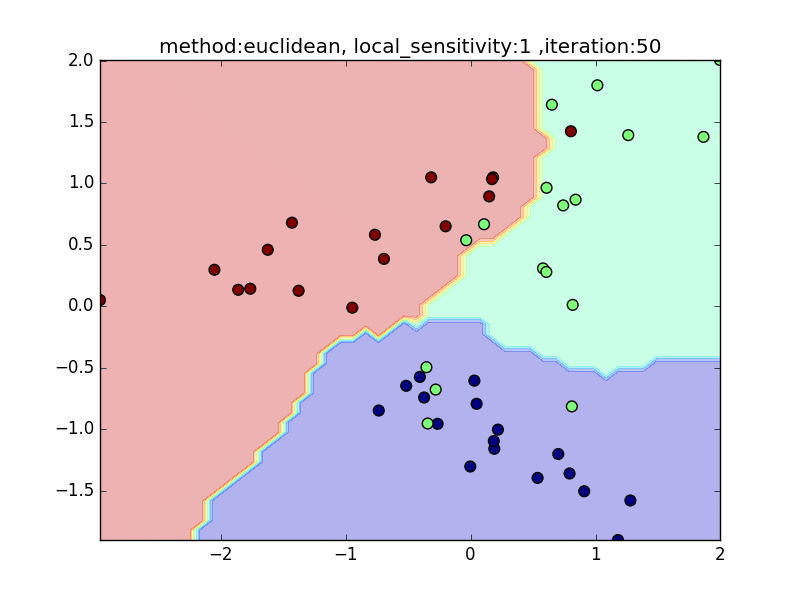
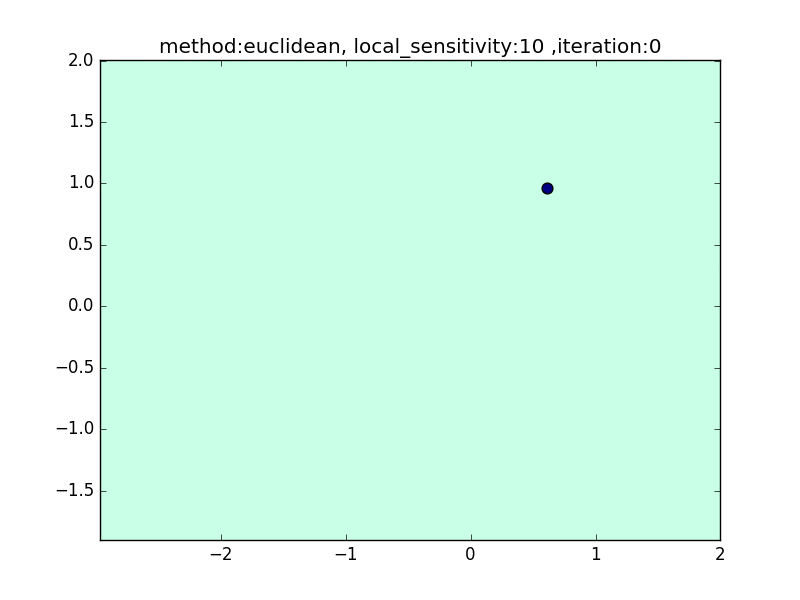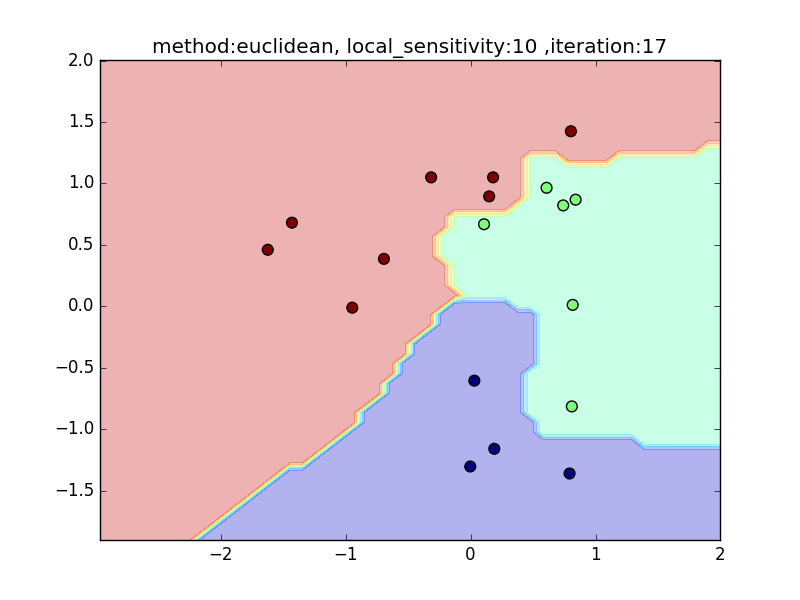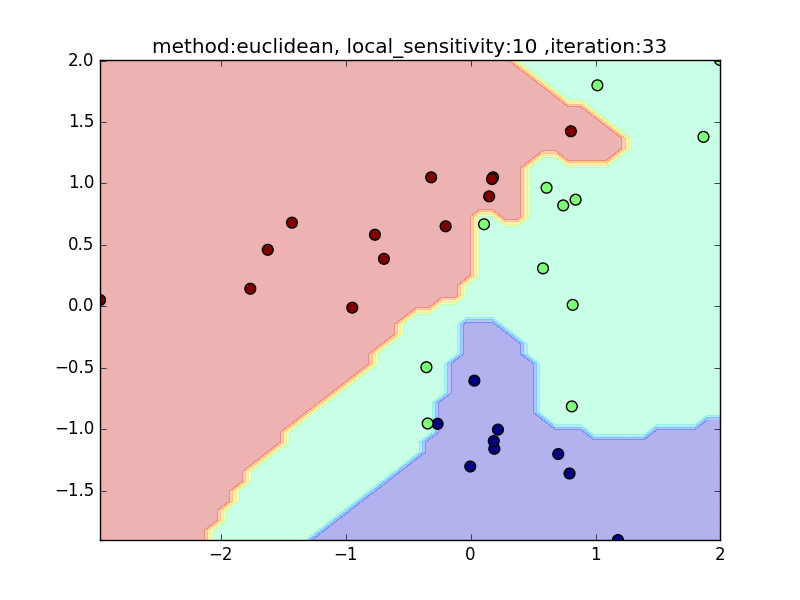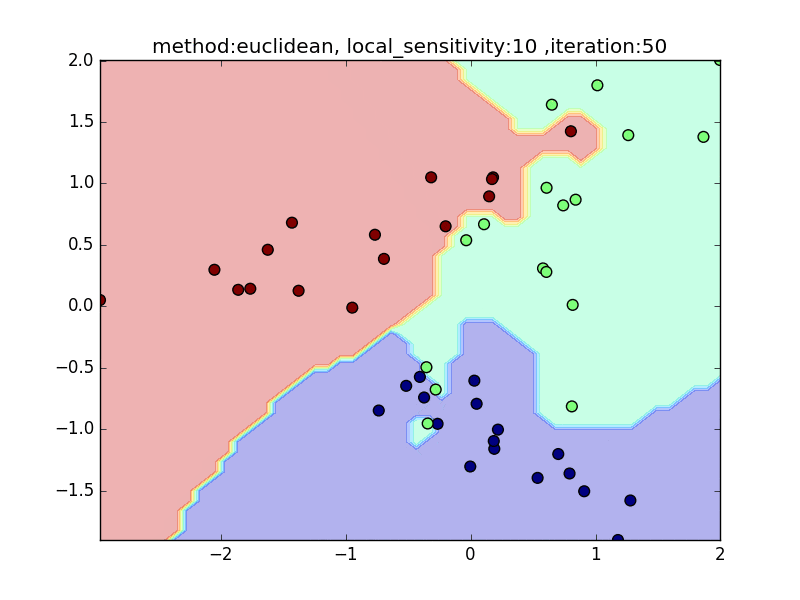
local_sensitivity
(distance : euclidean, nearest_neighbor_num = 5)
今度は、近傍点を固定してlocal_sensitivityを変えつつ、挙動を見てみます。
local_sensitivity = 10を見ればわかるように、近傍点を5個選んでいるのにもかかわらず、直近の点しかほとんど見ていないような挙動になっていることがわかると思います。
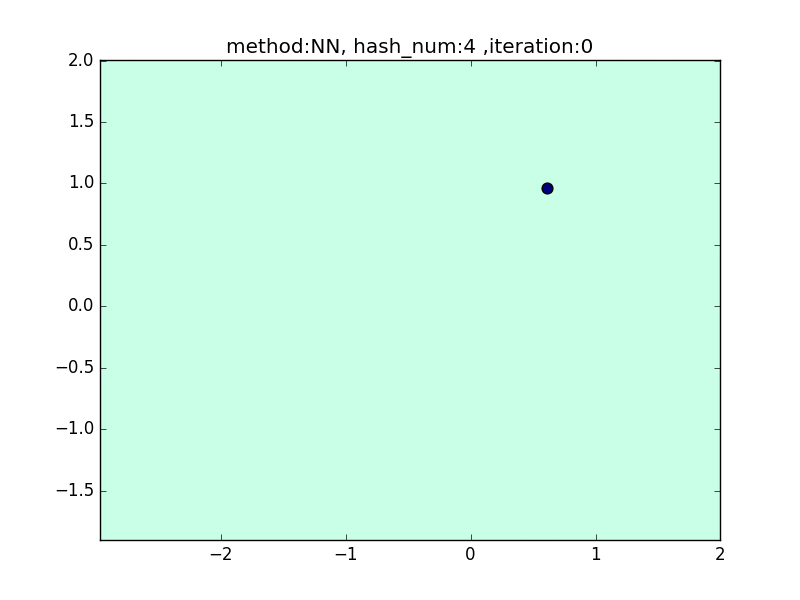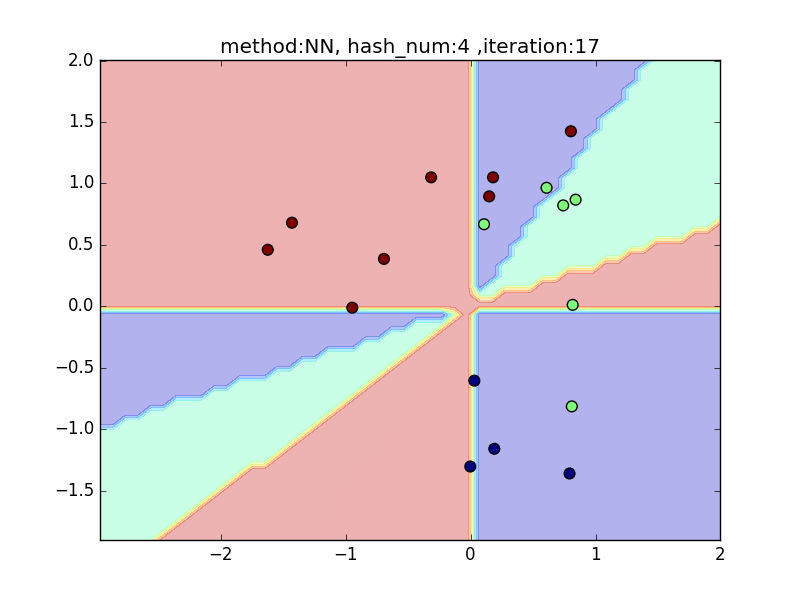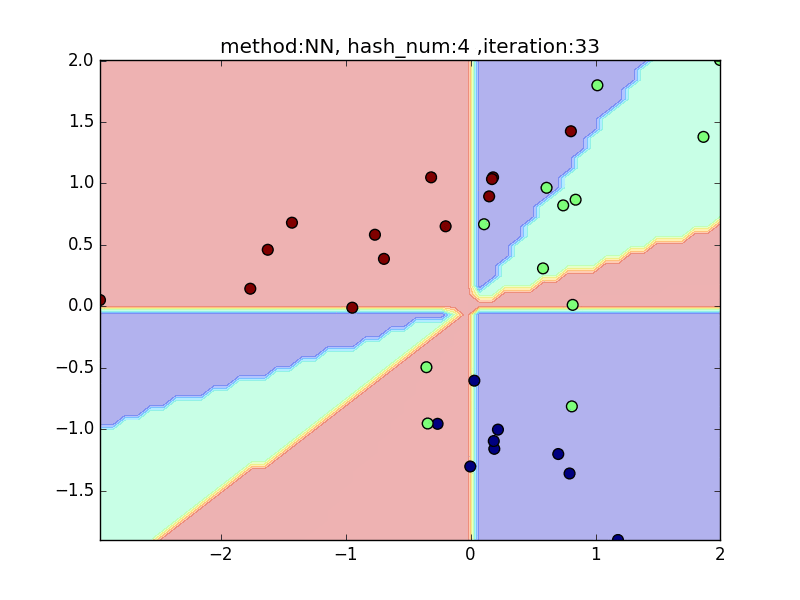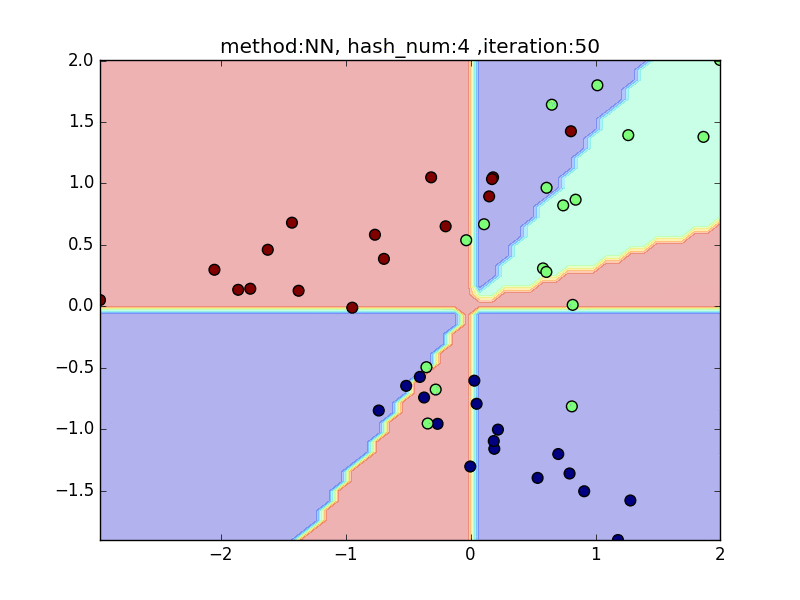
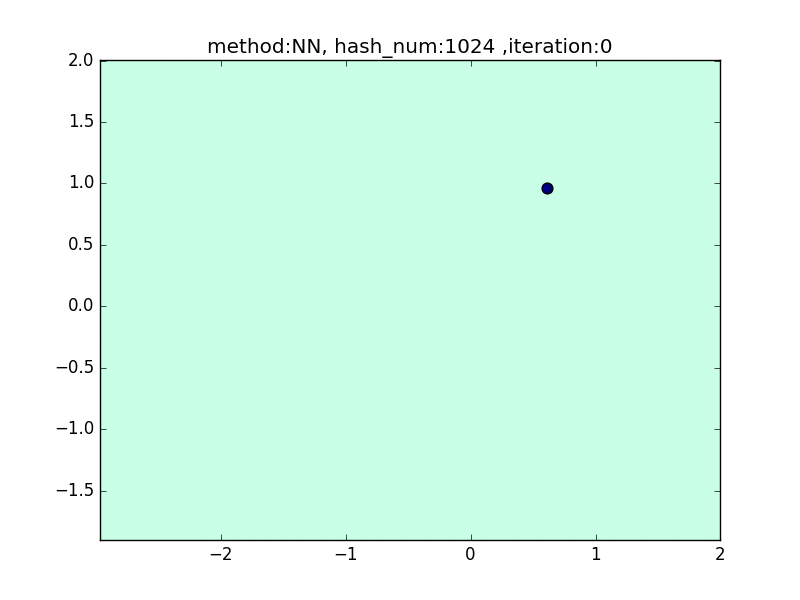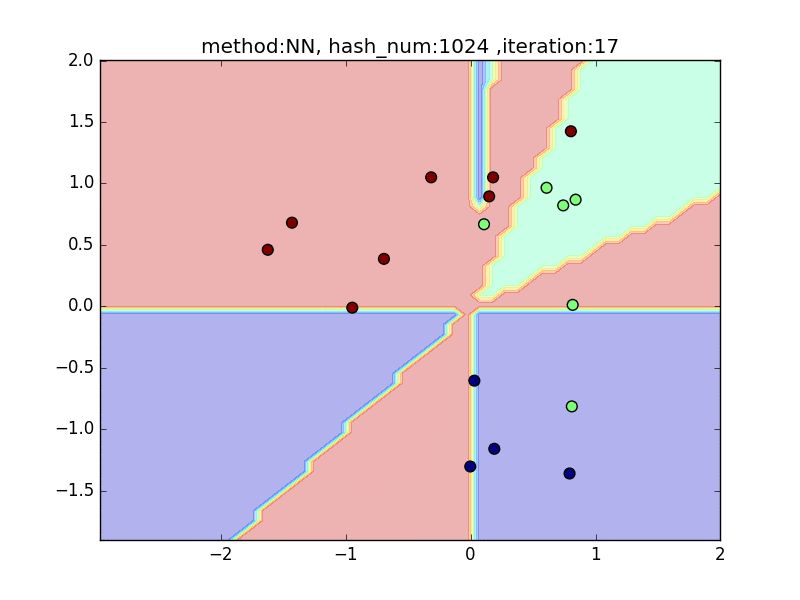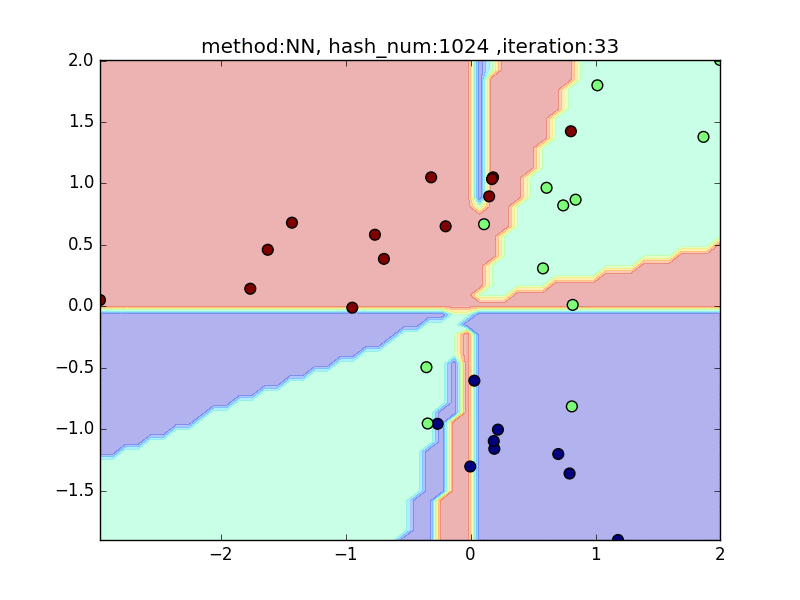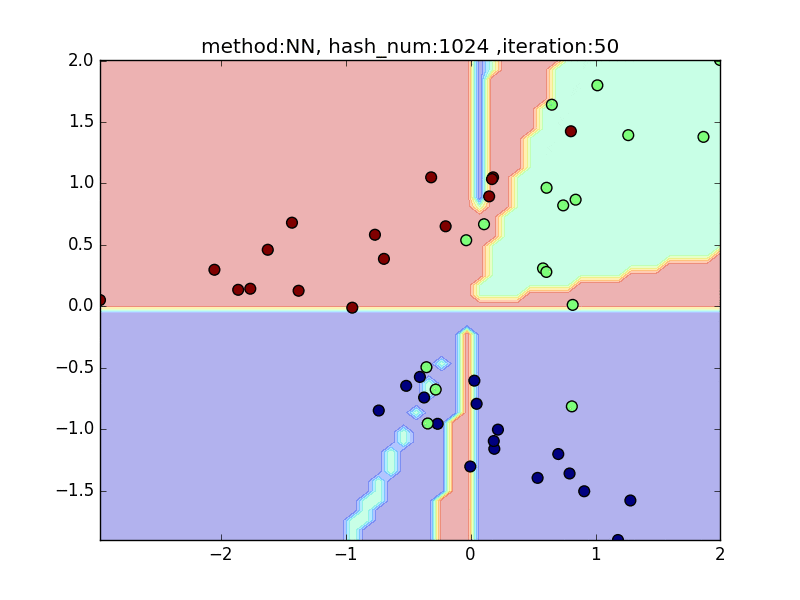
hash_num
(nearest_neighbor_num = 5, local_sensitivity = 1)
ハッシュの個数を指定して、挙動を見てみます。
hash_numが少ないと学習速度が速い分、近似精度が悪くなるというトレードオフがあります。
今回はminhashを例にとり見てみます。
やはり極端に少ないhash_numでは全然分類できておらず、
hash_numを増やすと精度が上がることが見て取れると思います。
hash_numと精度
これだけでは、どのくらい精度に差があるかわからないかもしれませんので、
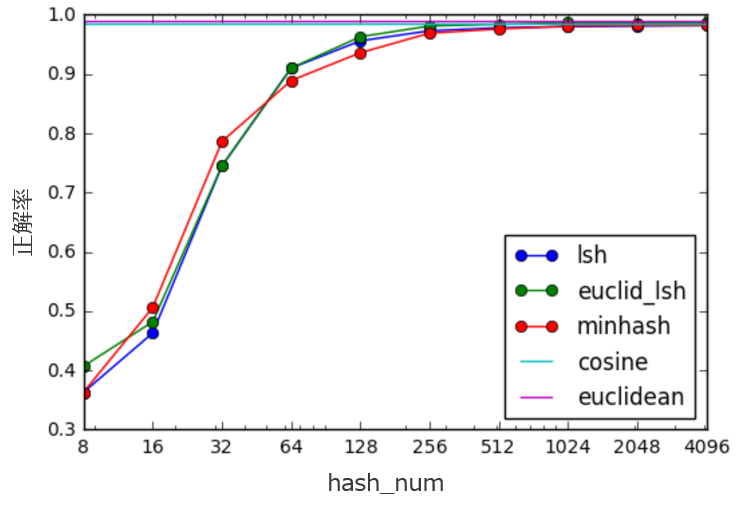
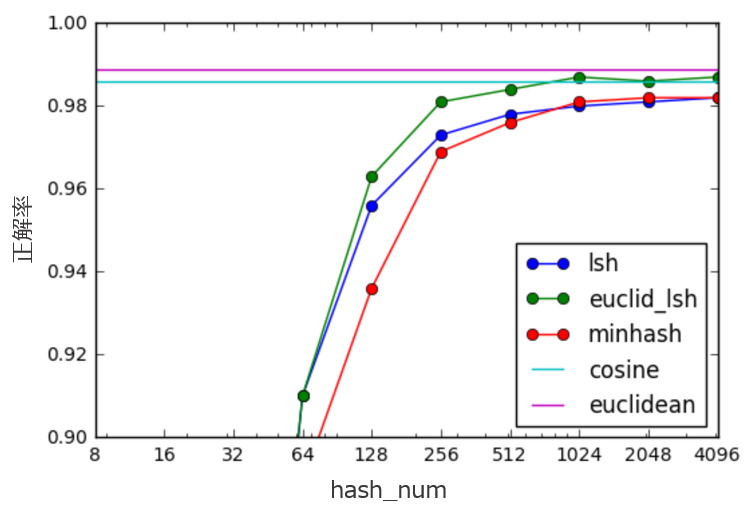
hash_numによる精度の変化を調べてみました。
-
評価 : Cross Validationを4回行い、正解率の平均
-
固定するパラメータ :
nearest_neighbor_num=5,local_sensitivity=1.0 -
hash_num={4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096}
これをみると、hash_num=256くらいで厳密計算のeuclideanやcosineと遜色ない精度を出せていることがわかります。
(これはデータセットによるところが大きいので、あくまで参考程度にしてください)
最適なパラメータを見つけるには
このように、パラメータによって挙動、精度が大きく変わるのですが、
「じゃあどのアルゴリズムとどのパラメータを使えばいいの?」
といわれると、なかなか難しいです。こういうのは、人の手で行うより機械にパラメータチューニングをして欲しいものなのですが、
Jubakitとscikit-learnを組み合わせれば、それができます!
@__john_smith__さんの記事で詳しく説明していただいていますが、
jubakitとhyperoptを使うことにより、
学習用のパラメータ最適化を行えるようになっています。
(詳細は、advent calendar 18日目をご覧ください)
このように、機械的にパラメータが見つけられるようになると、コストもグンと下がりますね!
まとめ
長くなりましたが、2日に渡って、分類器の中身を中心に説明してきました。
たまには中身のアルゴリズムに触れることで、機械学習に関する理解が深まり新たなアイディアが生まれるかもしれません。
さて、明日は誰が書いてくれるのでしょうか、楽しみです。