【完全展開】空間の平行四辺形の面積の成分表示

空間の平行四辺形の面積を求めるには下記のようにベクトルを使えば簡潔な公式で表せられます。

参考文献
基礎数学1 線型代数入門 齋藤正彦(著) 東京大学出版会

しかし、成分表示にしようと思うと、とてつない数の項(225項)が出てきて
手書きで計算など、とてもじゃないですがやってられません。
でも、やってみました。



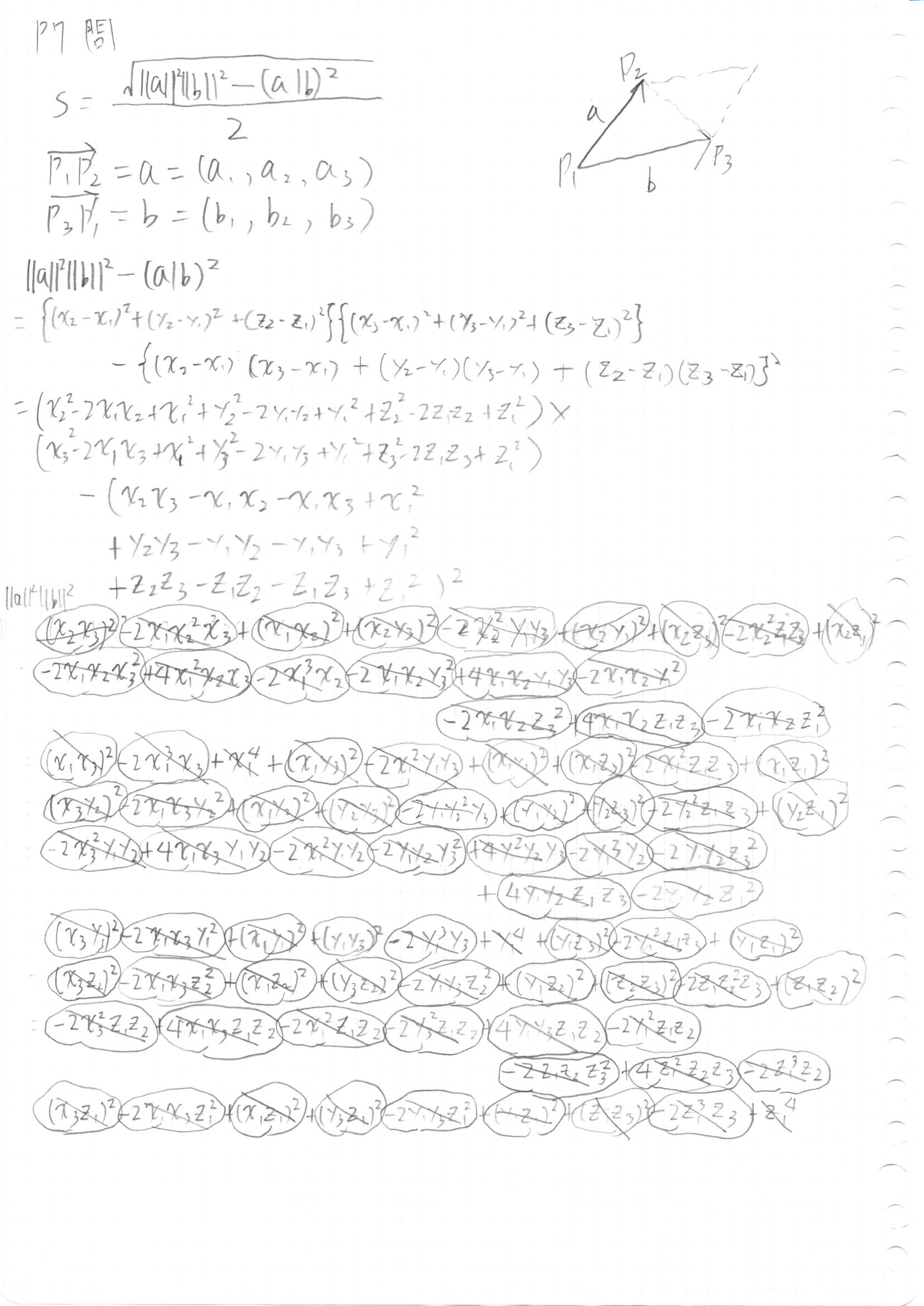
答え合わせをしたく、大分、検索してみましたが、こんな事をやってる人が見つかず
しょうがないので、自分でプログラムを書いて答え合わせしました。

# coding: utf-8

xyz = ['x_{1}', 'x_{2}', 'x_{3}', 'y_{1}', 'y_{2}', 'y_{3}', 'z_{1}', 'z_{2}', 'z_{3}']
dimention = 3;
element = len(xyz)

def mul(a_coefficient, a_term, b_coefficient, b_term):
    #係数
    coefficient = []
    #項
    term = []

    for a_n in range(len(a_coefficient)):
        for b_n in range(len(b_coefficient)):
            c = a_coefficient[a_n] * b_coefficient[b_n]
            t = [a_term[a_n][e] + b_term[b_n][e] for e in range(element)]

            #項整理
            if t in term:
                t_idx = term.index(t)
                coefficient[t_idx] += c
            else:
                coefficient.append(c)
                term.append(t)

    return coefficient, term

#||a||^2
#係数
aa_coefficient = []
#項
aa_term = []
#(x2-x1)^2 + (y2-y1)^2 + (z2-z1)^2
aa_coefficient_1 = [[-1,1], [-1,1], [-1,1]]
aa_term_1        = [[[1,0,0,0,0,0,0,0,0],[0,1,0,0,0,0,0,0,0]],[[0,0,0,1,0,0,0,0,0],[0,0,0,0,1,0,0,0,0]],[[0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,0]]]

for n in range(len(aa_coefficient_1)):
    aa_c, aa_t = mul(aa_coefficient_1[n], aa_term_1[n], aa_coefficient_1[n], aa_term_1[n])
    aa_coefficient = aa_coefficient + aa_c
    aa_term = aa_term + aa_t

#||b||^2
#係数
bb_coefficient = []
#項
bb_term = []
#(x3-x1)^2 + (y3-y1)^2 + (z3-z1)^2
bb_coefficient_1 = [[-1,1], [-1,1], [-1,1]]
bb_term_1        = [[[1,0,0,0,0,0,0,0,0],[0,0,1,0,0,0,0,0,0]],[[0,0,0,1,0,0,0,0,0],[0,0,0,0,0,1,0,0,0]],[[0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,0,1]]]

for n in range(len(bb_coefficient_1)):
    bb_c, bb_t = mul(bb_coefficient_1[n], bb_term_1[n], bb_coefficient_1[n], bb_term_1[n])
    bb_coefficient = bb_coefficient + bb_c
    bb_term = bb_term + bb_t

#||a||^2||b||^2
aabb_coefficient, aabb_term = mul(aa_coefficient, aa_term, bb_coefficient, bb_term)

#(a|b)
#係数
ab_coefficient = []
#項
ab_term = []
#(x2-x1)(x3-x1) + (y2-y1)(y3-y1) + (z2-z1)(z3-z1)
for n in range(len(aa_coefficient_1)):
    ab_c, ab_t = mul(aa_coefficient_1[n], aa_term_1[n], bb_coefficient_1[n], bb_term_1[n])
    ab_coefficient = ab_coefficient + ab_c
    ab_term = ab_term + ab_t

#(a|b)^2
abab_coefficient, abab_term = mul(ab_coefficient, ab_term, ab_coefficient, ab_term)

#||a||^2||b||^2-(a|b)^2
coefficient = aabb_coefficient
term = aabb_term

for abab_n in range(len(abab_coefficient)):
    if abab_term[abab_n] in term:
        t_idx = term.index(abab_term[abab_n])
        coefficient[t_idx] -= abab_coefficient[abab_n]
    else:
        coefficient.append(-abab_coefficient[abab_n])
        term.append(abab_term[abab_n])

print(coefficient)
print(term)

#Markdown形式出力
for n in range(len(coefficient)):
    if coefficient[n] != 0:

        exponential = ''
        for e in range(element):
            if term[n][e] != 0:
                if term[n][e] == 1:
                    exponential += xyz[e]
                else:
                    exponential += xyz[e] + '^' + str(term[n][e])

        if coefficient[n] == 1:
            print('+' + exponential)
        else:
            print('{:+}'.format(coefficient[n]) + exponential)

出力はこうなります。

\begin{align}
&\|a\|^2\|b\|^2-(a|b)^2 = \\
&x_{1}^2y_{3}^2
+x_{1}^2z_{3}^2
+2x_{1}x_{2}y_{1}y_{3}
-2x_{1}x_{2}y_{3}^2
+2x_{1}x_{2}z_{1}z_{3}
-2x_{1}x_{2}z_{3}^2
+x_{2}^2y_{1}^2 \\
&-2x_{2}^2y_{1}y_{3}
+x_{2}^2y_{3}^2
+x_{2}^2z_{1}^2
-2x_{2}^2z_{1}z_{3}
+x_{2}^2z_{3}^2
+x_{3}^2y_{1}^2
+y_{1}^2z_{3}^2 \\
&+2x_{1}x_{3}y_{1}y_{2}
-2x_{3}^2y_{1}y_{2}
+2y_{1}y_{2}z_{1}z_{3}
-2y_{1}y_{2}z_{3}^2
+x_{1}^2y_{2}^2
-2x_{1}x_{3}y_{2}^2
+x_{3}^2y_{2}^2 \\
&+y_{2}^2z_{1}^2
-2y_{2}^2z_{1}z_{3}
+y_{2}^2z_{3}^2
+x_{3}^2z_{1}^2
+y_{3}^2z_{1}^2
+2x_{1}x_{3}z_{1}z_{2}
-2x_{3}^2z_{1}z_{2} \\
&+2y_{1}y_{3}z_{1}z_{2}
-2y_{3}^2z_{1}z_{2}
+x_{1}^2z_{2}^2
-2x_{1}x_{3}z_{2}^2
+x_{3}^2z_{2}^2
+y_{1}^2z_{2}^2
-2y_{1}y_{3}z_{2}^2 \\
&+y_{3}^2z_{2}^2
-2x_{1}^2y_{2}y_{3}
-2x_{1}^2z_{2}z_{3}
-2x_{1}x_{3}y_{1}y_{3}
+2x_{1}x_{3}y_{2}y_{3}
-2x_{1}x_{3}z_{1}z_{3}
+2x_{1}x_{3}z_{2}z_{3} \\
&-2x_{1}x_{2}y_{1}y_{2}
+2x_{1}x_{2}y_{2}y_{3}
-2x_{1}x_{2}z_{1}z_{2}
+2x_{1}x_{2}z_{2}z_{3}
-2x_{2}x_{3}y_{1}^2
+2x_{2}x_{3}y_{1}y_{3}
+2x_{2}x_{3}y_{1}y_{2} \\
&-2x_{2}x_{3}y_{2}y_{3}
-2x_{2}x_{3}z_{1}^2
+2x_{2}x_{3}z_{1}z_{3}
+2x_{2}x_{3}z_{1}z_{2}
-2x_{2}x_{3}z_{2}z_{3}
-2y_{1}^2z_{2}z_{3}
-2y_{1}y_{3}z_{1}z_{3} \\
&+2y_{1}y_{3}z_{2}z_{3}
-2y_{1}y_{2}z_{1}z_{2}
+2y_{1}y_{2}z_{2}z_{3}
-2y_{2}y_{3}z_{1}^2
+2y_{2}y_{3}z_{1}z_{3}
+2y_{2}y_{3}z_{1}z_{2}
-2y_{2}y_{3}z_{2}z_{3}
\end{align}

63項に整理されます。

因数分解して整理できそうな気配がします。
しかし、さすがにこれ以上、地道に因数分解はしんど過ぎますので
天下り的にはなってしまいますが、外積による面積の公式から

出展
理数アラカルト 外積の大きさは平行四辺形の面積に等しい

下記のようになるのだろうと思われます。

\begin{align}
S^2= \ &\{(y_{2}-y_{1})(z_{3}-z_{1})-(z_{2}-z_{1})(y_{3}-y_{1})\}^2+ \\
&\{(z_{2}-z_{1})(x_{3}-x_{1})-(x_{2}-x_{1})(z_{3}-z_{1})\}^2+ \\
&\{(x_{2}-x_{1})(y_{3}-y_{1})-(y_{2}-y_{1})(x_{3}-x_{1})\}^2
\end{align}

反響を頂けるようでしたら平面についても記事を投稿しようかと思います。