機械学習で四則演算 3【積 失敗1】

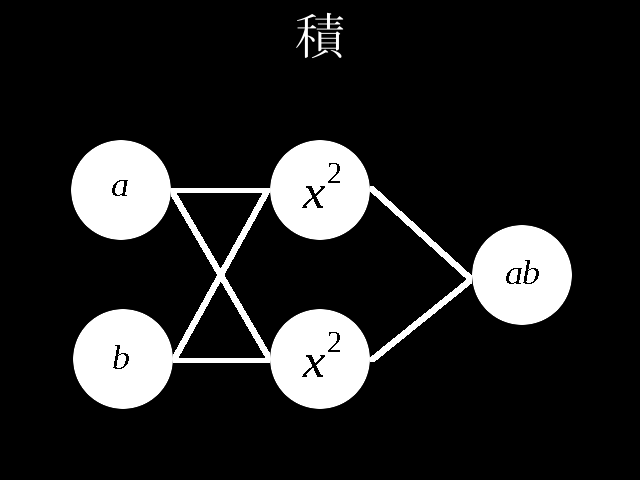
深層学習の形式でかけ算をする回路を考えてみました。\\
重みを\\
w[0]=
\begin{pmatrix}
1 & 1\\
1 & -1
\end{pmatrix}
w[1]=
\begin{pmatrix}
0.25\\
-0.25
\end{pmatrix}\\
としますとかけ算ができます。\\
　\\
\begin{pmatrix}
a & b
\end{pmatrix}
\begin{pmatrix}
1 & 1\\
1 & -1
\end{pmatrix}
=
\begin{pmatrix}
a+b & a-b
\end{pmatrix}\\
\begin{pmatrix}
a+b & a-b
\end{pmatrix}
を活性化関数
\begin{pmatrix}
x^2 & x^2
\end{pmatrix}
へ入力し
\begin{pmatrix}
(a+b)^2 & (a-b)^2
\end{pmatrix}\\
\begin{pmatrix}
(a+b)^2 & (a-b)^2
\end{pmatrix}
=
\begin{pmatrix}
a^2+2ab+b^2 & a^2-2ab+b^2
\end{pmatrix}\\
\begin{pmatrix}
a^2+2ab+b^2 & a^2-2ab+b^2
\end{pmatrix}
\begin{pmatrix}
0.25\\
-0.25
\end{pmatrix}
=ab\\
　\\
重みの初期値を乱数で決めてから学習を繰り返すと\\
w[0]=
\begin{pmatrix}
1 & 1\\
1 & -1
\end{pmatrix}
w[1]=
\begin{pmatrix}
0.25\\
-0.25
\end{pmatrix}
になるのか試してみました。

        string path = @"D:\開発\AI\" + DateTime.Now.ToString("yyyyMMdd") + "積.csv";
        double[][,] w = new double[2][,];

        int In = 2;
        //int layer = 1;
        int cell = 2;
        //int bias = 0;
        int Out = 1;
        
        Stopwatch sw = new Stopwatch();
        delegate void dldl();

        private void button1_Click(object sender, EventArgs e)
        {
            button1.Enabled = false;
            sw.Start();
            Thread th = new Thread(nnw);
            th.Start();
        }

        private void nnw()
        {
            //列見出し
            string row_title = ",a,b,ab,";
            for (int n1 = 0; n1 < In; n1++)
            {
                for (int n2 = 0; n2 < cell; n2++)
                {
                    row_title += "w[0][" + n1 + "_" + n2 + "],";
                }
            }
            for (int n = 0; n < cell; n++)
            {
                row_title += "h_in[" + n + "],h_out[" + n + "],";
            }
            for (int n1 = 0; n1 < cell; n1++)
            {
                for (int n2 = 0; n2 < Out; n2++)
                {
                    row_title += "w[1][" + n1 + "_" + n2 + "],";
                }
            }
            row_title += "Y,ΔE";
            using (StreamWriter sw = new StreamWriter(path, true, Encoding.Unicode))
            {
                sw.Write(row_title + Environment.NewLine);
            }

            //重み初期設定
            w[0] = new double[In, cell];            
            w[1] = new double[cell, Out];
            
            Random cRandom = new Random();// 0.0 以上 1.0 以下の乱数を取得
            //RNGCryptoServiceProvider rng = new RNGCryptoServiceProvider();
            //byte[] bs = new byte[sizeof(int)];
            for (int n0 = 0; n0 < w.Length; n0++)
            {
                for (int n1 = 0; n1 < w[n0].GetLength(0); n1++)
                {
                    for (int n2 = 0; n2 < w[n0].GetLength(1); n2++)
                    {
                        w[n0][n1, n2] = cRandom.NextDouble();
                        //rng.GetBytes(bs);
                        //w[n0][n1, n2] = BitConverter.ToInt32(bs, 0);
                    }
                }
            }

            //学習
            for (int p = 1; p <= 1000; p++)
            {
                //入力値設定
                double a = cRandom.NextDouble();
                double b = cRandom.NextDouble();
                //rng.GetBytes(bs);
                //double a = BitConverter.ToInt32(bs, 0);
                //rng.GetBytes(bs);
                //double b = BitConverter.ToInt32(bs, 0);

                //教師信号
                double a_mul_b = a * b;

                //順伝播
                double[] h_in = new double[cell];
                double[] h_out = new double[cell];

                for (int n = 0; n < cell; n++)
                {//入力
                    h_in[n] = a * w[0][0, n] + b * w[0][1, n];
                    h_out[n] = h_in[n] * h_in[n];
                }

                double Y = 0;
                for (int cl = 0; cl < cell; cl++)
                {//出力
                    Y += h_out[cl] * w[1][cl, 0];
                }

                //二乗誤差
                double dE = Y - a_mul_b;//計算省略のため二乗誤差微分後の値

                //記録
                string rec = p.ToString() + "," + a.ToString() + "," + b.ToString() + "," + a_mul_b.ToString() + ",";
                for (int n1 = 0; n1 < w[0].GetLength(0); n1++)
                {
                    for (int n2 = 0; n2 < w[0].GetLength(1); n2++)
                    {
                        rec += w[0][n1, n2].ToString() + ",";
                    }
                }
                for (int n = 0; n < cell; n++)
                {
                    rec += h_in[n].ToString() + "," + h_out[n].ToString() + ",";
                }
                for (int n1 = 0; n1 < w[1].GetLength(0); n1++)
                {
                    for (int n2 = 0; n2 < w[1].GetLength(1); n2++)
                    {
                        rec += w[1][n1, n2].ToString() + ",";
                    }
                }
                rec += Y.ToString() + "," + dE.ToString();
                using (StreamWriter sw = new StreamWriter(path, true, Encoding.Unicode))
                {
                    sw.Write(rec + Environment.NewLine);
                }

                //逆伝播
                //∂E/∂In                       
                double[] dE_dI = new double[cell];
                for (int cl = 0; cl < cell; cl++)
                {
                    dE_dI[cl] = 2 * h_in[cl] * w[1][cl, 0] * dE;
                }
                //w-Δw
                for (int cl = 0; cl < cell; cl++)
                {
                    w[0][0, cl] = w[0][0, cl] - (a * dE_dI[cl]);
                    w[0][1, cl] = w[0][1, cl] - (b * dE_dI[cl]);
                }
                for (int cl = 0; cl < cell; cl++)
                {
                    w[1][cl, 0] = w[1][cl, 0] - (h_out[cl] * dE);
                }
            }

            //最終記録
            string last_rec = new string(',', In + Out + 1);
            for (int n1 = 0; n1 < w[0].GetLength(0); n1++)
            {
                for (int n2 = 0; n2 < w[0].GetLength(1); n2++)
                {
                    last_rec += w[0][n1, n2].ToString() + ",";
                }
            }
            last_rec += new string(',', cell * 2);
            for (int n1 = 0; n1 < w[1].GetLength(0); n1++)
            {
                for (int n2 = 0; n2 < w[1].GetLength(1); n2++)
                {
                    last_rec += w[1][n1, n2].ToString() + ",";
                }
            }
            last_rec += new string(',', Out * 2 - 1);
            using (StreamWriter sw = new StreamWriter(path, true, Encoding.Unicode))
            {
                sw.Write(last_rec);
            }

            //読取専用
            File.SetAttributes(path, FileAttributes.ReadOnly);

            Invoke(new dldl(delegate
            {
                sw.Stop();
                label1.Text = sw.Elapsed.ToString();
                button1.Enabled = true;
            }));

        }

乱数で重みの初期値が\\
w[0]=
\begin{pmatrix}
0.109293425972244 & 0.342316406472733\\
0.24016019340612 & 0.377903668385886
\end{pmatrix}
w[1]=
\begin{pmatrix}
0.497233796630629\\
0.071685814332071
\end{pmatrix}
と決定され\\
1000回学習させてみました。\\
なにはともあれ、まずは重みの推移グラフをご覧下さい。

桁が文字通り、桁違いにおかしいです。
どうやら、学習を200回越えたあたりで何かあったようなのでデータを見てみる事にします。

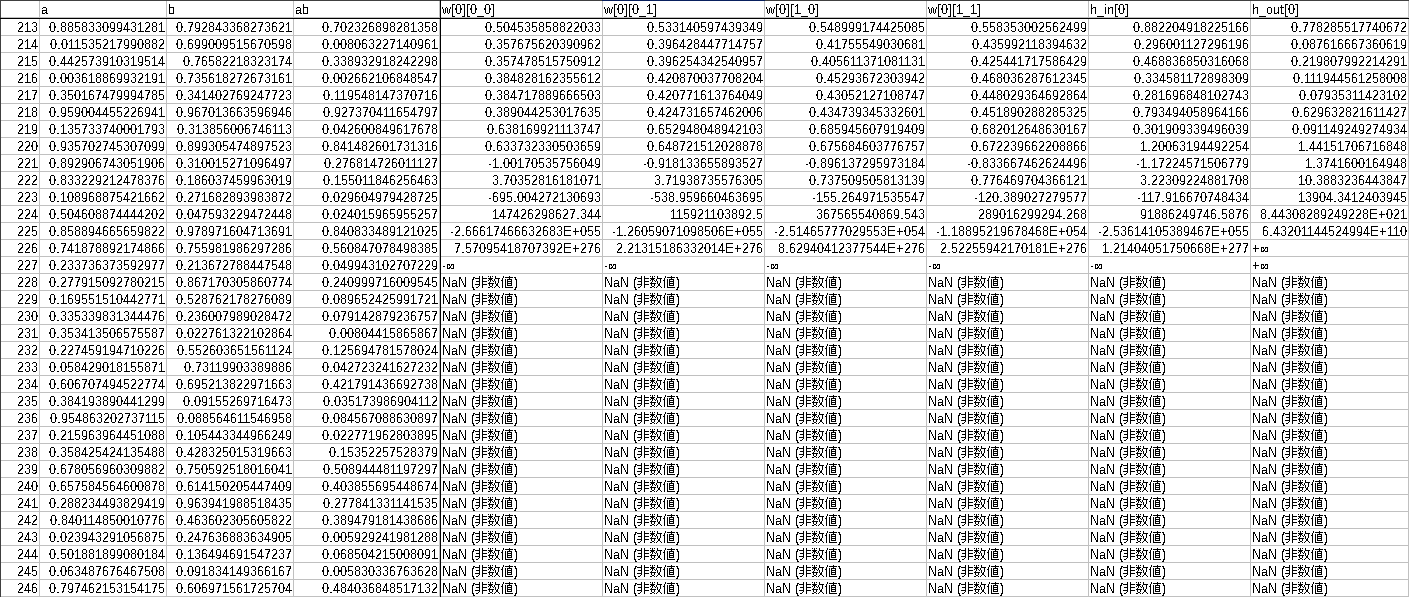
途中でオーバーフローを起して学習もへったくれも無い状態になってしまいました。
何でこんなことになってしまったのか。これが、過学習というやつでしょうか。
どうしたものか
とりあえず、200回学習させたところまではどんなグラフになるのかを見る事にしました。

どうも、目標の値に収束する気配は無く、全ての重みが同調して推移している様子が見て取れました。
原因をつきとめる為、w[1]の重みは固定しw[0]だけ、2000回学習させてみることにしました。

初期値\\
w[0]=
\begin{pmatrix}
0.773612595057866 & 0.487146192457129\\
0.305395017985904 & 0.674572251585579
\end{pmatrix}\\
目標値\\
w[0]=
\begin{pmatrix}
1 & 1\\
1 & -1
\end{pmatrix}\\
計算値\\
w[0]=
\begin{pmatrix}
0.943032192695527 & -0.940468591037847\\
1.06007360784422 & 1.05778446754946
\end{pmatrix}

このような結果になりました。
計算値は収束しているのですが、目標値とずれてしまいました。
また、-1に当たる部分が別の部分になってしまいまいました。
しかし、この重みでも回路に入力すると目的のかけ算の値が出力されます。
考えましたところ、下記条件を満たせば積が出力されるとわかりました。

w[0]=
\begin{pmatrix}
△ & ▲\\
□ & ■
\end{pmatrix}\\
△=▲　かつ　□=-■　かつ　△□=1\\
または\\
△=-▲　かつ　□=■　かつ　△□=1\\
もしかしたら対称性からもっとあるかもしれません。

冒頭で示した回路では重みが一意に定まらない回路だから
学習を繰り返すと重みが混乱し狂喜乱舞してしまったのかと思いましたが
どうも、そういう事でもなさそうです。

次に、w[0]を固定しw[1]がどう変化するか、2000回学習させて確かめてみました。

目標値\\
w[1]=
\begin{pmatrix}
0.25\\
-0.25
\end{pmatrix}\\
初期値\\
w[1]=
\begin{pmatrix}
0.146244229351284\\
0.840737492237584
\end{pmatrix}\\
計算値\\
w[1]=
\begin{pmatrix}
-4.52155444931984E+073\\
4.02666751918411E+074
\end{pmatrix}

何でこんなに暴れるのか、私の教育はどこが間違っていたのか
そんなに苦労をかけて育てたつもりはありません。
無理矢理、型にはめようとしたからなのか
もっと、この子の個性を尊重すればよかったのだろうか
私のAIがたりなかったからなのでしょうか。
もう、疲れました。眠ります。

次回
積 失敗2 学習率導入