再帰構造、右から見るか？左から見るか？

最近、サイエンス社の『プログラミングの基礎』を読み進めています。
タイトルは完全にプログラミング入門本なんですが、初学者にいきなりOCamlを叩き込もうという類の本なので、私のような関数型初心者にもぴったり。

以下はそんなOCaml入門中の私の思考メモです。
マサカリ大歓迎。

tl; dr

「まとめ」まで飛んでください。

foldに着目する

リスト処理関係の高階関数っていっぱいありますよね。
mapとか、filterとかよく使います。

foldはその次ぐらいによく使うやつ、みたいに今までは思っていました。
でも、この辺の関数を全部自分で再実装してみて気づきました。
foldだけなんだか格が違うんです。
というか抽象度が違う。
わかりやすく言えば、こいつだけ汎用性が高すぎるんです。

というのも、mapもfilterもfoldで書けるんですよね。
逆はちょっと今の自分には思いつかないです。

my_map.ml

let my_map f a_list =
  List.fold_right
    (fun item acm -> (f item) :: acm)
    a_list
    []

my_filter.ml

let my_filter f a_list =
  List.fold_right
    (fun item acm -> if f item then item :: acm else acm)
    a_list
    []

どうやら、foldは他の多くの再帰処理の基盤になっていると言ってよさそうです。

fold_rightとfold_left

そんなfoldを実際に実装して、左右の違いを比べてみます。

my_fold_right.ml

let rec my_fold_right f a_list default = match a_list with
    [] -> default
  | first :: rest -> f first (my_fold_right f rest default)

my_fold_left.ml

let rec my_fold_left f default a_list = match a_list with
    [] -> default
  | first :: rest -> my_fold_left f (f default first) rest

fold_leftはdefaultに渡す値を変えていくのがテクいですね。

以下の具体例について、実際の処理を比べてみます。

my_fold_sample.ml

let sum_right = my_fold_right (+) [1; 10; 100] 5
(* val sum_right : int = 116 *)

let sum_left = my_fold_left (+) 5 [1; 10; 100]
(* val sum_left : int = 116 *)

それぞれ以下のように処理が進んでいるはずです。
（注：f 10 20は即ち10 + 20です。）

fold_right.txt

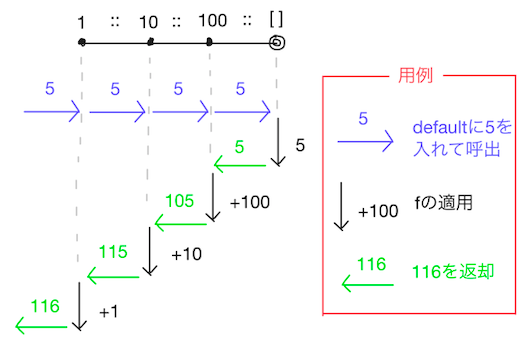
  fold_right f [1; 10; 100] 5
= f 1 (fold_right f [10; 100] 5)
= f 1 (f 10 (fold_right f [100] 5))
= f 1 (f 10 (f 100 (fold_right f [] 5)))
= f 1 (f 10 (f 100 5))
= f 1 (f 10 105)
= f 1 115
= 116

fold_left.txt

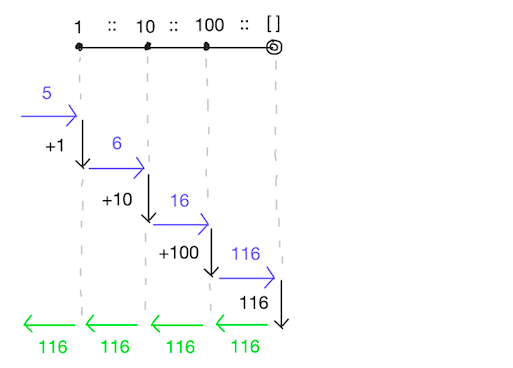
  fold_left f 5 [1; 10; 100]
= fold_left f (f 5 1) [10; 100]
= fold_left f 6 [10; 100]
= fold_left f (f 6 10) [100]
= fold_left f 16 [100]
= fold_left f (f 16 100) []
= fold_left f 116 []
= 116

図で表すと以下のようになります。

• fold_right

• fold_left

さて、「foldは多くの再帰処理の基盤」ということで、この分析はもう少し一般に広げられるポテンシャルがあるように感じられます。

「右から再帰」と「左から再帰」

fold_rightとfold_leftの処理内容を、少し抽象化してまとめてみます。

• 前提
  • 再帰的なデータ構造をしている評価対象について、基底部（再帰呼出が止まる部分です。上の例で言えば[]。）を右端、評価したい部分を左端と捉える。
• fold_right（＝右から再帰）
  • 右端について評価し、その評価結果を利用して1つ左を求めることを繰り返しながら、左端に至る。
• fold_left（＝左から再帰）
  • 左端から順に評価結果を蓄積し、右端に至れば終了する。

抽象化したそれぞれの定義に、「右から再帰」「左から再帰」と名前をつけました。

fold以外の「右から再帰」「左から再帰」を実際に見てみましょう。
みんな大好き階乗計算です。
自然数は1を基底とした再帰的データ構造と見ることができます。

fact_right.ml

let rec fact_right n default =
  if n <= 1 then default else n * fact_right (n - 1) default

let test1 = fact_right 1 1 = 1
let test2 = fact_right 5 1 = 120

fact_left.ml

let rec fact_left default n =
  if n <= 1 then default else fact_left (default * n) (n - 1)

let test1 = fact_left 1 1 = 1
let test2 = fact_left 1 5 = 120

で、どっちを使えば良いの？

いよいよ本題。
上記の図やコードを踏まえて、メリット・デメリットを自分なりに洗い出してみました。

最左値／最右値が欲しい時

当たり前ですが、「条件を満たす中で最も左／右の値が欲しい時」などは、やはり左／右から再帰していった方が早いでしょう。
例えば、JavaScriptでいうところのArray.prototype.indexOf()は「左から再帰」、Array.prototype.lastIndexOf()は「右から再帰」で実装することになります。

基底値定義の埋め込み

上で書いた階乗計算ですが、普通に考えたら階乗の基底値の定義（1!）は1に決まっています。
パラメータ化する意味はありません。
なので関数の中に定義を埋め込みたいところです。

「右から再帰」で書かれた階乗だと、普通に埋め込むことができます。

fact_right_default_fixed.ml

let rec fact_right_default_fixed n =
  if n <= 1 then 1 else n * fact_right_default_fixed (n - 1)

let test1 = fact_right_default_fixed 1 = 1
let test2 = fact_right_default_fixed 5 = 120

しかし、「左から再帰」の場合は埋め込みが難しいです。
なぜでしょうか？

fact_right 5 1を呼んだ時、再帰呼出部だけを抜き出すと
fact_right 4 1、
fact_right 3 1、
fact_right 2 1、
fact_right 1 1となります。

ところが
fact_left 1 5を呼ぶ時は、再帰呼出部は
fact_left 5 4
fact_left 20 3
fact_left 60 2
fact_left 120 1です。

つまり、
fact_right n defaultの引数defaultが純粋に基底値であるのに対し、
fact_left default nの引数defaultは実はアキュムレーターの役割を担っているわけです。（defaultという命名が良くなかったですね。）

これを踏まえると、fact_leftの場合は引数defaultを残さないといけないことが分かります。
なので、補助関数を用いない限り定義を埋め込めないということになります。

fact_left_default_fixed.ml

let fact_left_default_fixed n =
  let rec fact_left default n =
    if n <= 1 then default else fact_left (default * n) (n - 1)
  in fact_left 1 n

let test1 = fact_left_default_fixed 1 = 1
let test2 = fact_left_default_fixed 5 = 120

自然さ、分かりやすさ

fact_right 5 1は、
fact_right 4 1（＝4!）、
fact_right 3 1（＝3!）、
fact_right 2 1（＝2!）、
fact_right 1 1（＝1!）でできています。
それぞれの呼出が独立した数学的な意味を持っています。

一方で、fact_left 1 5の途中の呼出、
例えばfact_left 20 3なんかは、はっきり言って「20ってなんやねん」という話になってきます。
この20はアキュムレーター、要は計算の都合で出てきただけの値です。
fact_left 20 3という式は、fact_left 1 5を求める時にしか役に立たないわけです。

こうして比較してみると、やはり「右から再帰」の方が圧倒的にシンプルで分かりやすいと思います。

「右から再帰」は、独立した意味のある数学的定義のみを使って定義する。
それに対し「左から再帰」は、アキュムレーターという計算のプロセスを意識しないといけない。

まあしかし、for文的な思考を好む人にとってはもしかしたら「左から再帰」の方が分かりやすいのかもしれませんね。

パフォーマンス

「左から再帰」は末尾再帰です。
末尾再帰最適化のある言語なら恩恵を受けられます。

一方で、メモ化を多用するなら「右から再帰」の方が良さそうです。
例えばfact_right 5 1をメモ化しながら計算すれば、そのあとにfact_right 3 1を呼び出す時にも恩恵を受けられます。
fact_left 1 5をしてしまった場合、メモ化されるのはfact_left 20 3の結果であり、そのあとにfact_left 1 3を呼び出しても恩恵は受けられません。

評価を見ながら動的に再帰呼出を止めたい

• 基底まで行かなくても評価が確定する。
• 評価結果を見ないと基底かどうか判断がつかない。

とかですかね。
後者の例は思いつきませんが、前者の例はexists（1つ見つければtrueで確定する）や、リストの全ての値をかけ算する（0が出てきた瞬間0で確定する）などが考えられます。

これが実現できるのは「左から再帰」のみです。
「右から再帰」の場合、例えばかけ算の例なら「再帰呼出の結果が0の場合、かけ算を行わずに0をそのまま返す」という風に評価処理を節約することはできますが、呼出自体は節約できていませんし、コードも汚くなりがちです。

言葉で書くと分かりづらいので、コードと図でも示します。
引き続きかけ算の例です。

product_left.ml

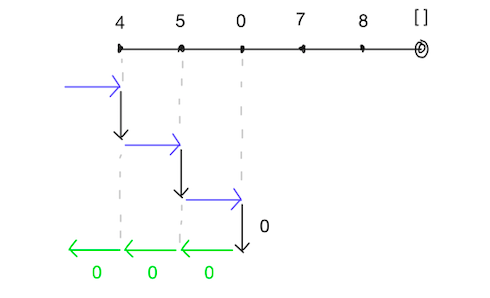
let rec product_left default a_list = match a_list with
    [] -> default
  | first :: rest ->
    if first = 0 then 0
    else product_left (default * first) rest

let test1 = product_left 1 [4; 5; 6; 7; 8] = 6720
let test2 = product_left 1 [4; 5; 0; 7; 8] = 0

product_right.ml

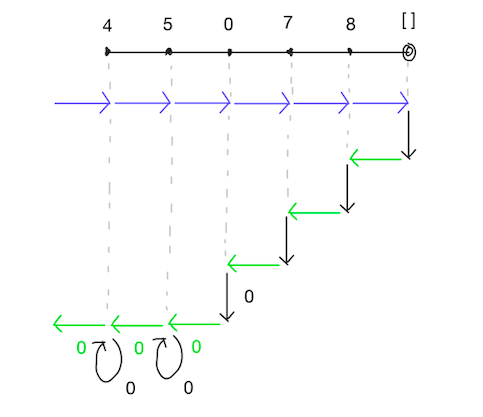
let rec product_right a_list default = match a_list with
    [] -> default
  | first :: rest ->
    let rest_product = product_right rest default
    in if rest_product = 0 then 0
    else first * rest_product

let test1 = product_right [4; 5; 6; 7; 8] 1 = 6720
let test2 = product_right [4; 5; 0; 7; 8] 1 = 0

• product_left

• product_right

比較しやすいよう、基底値定義は両方とも外出しにしました。
product_rightの方は、これだともう愚直に0をかけ続けた方がマシな気がします。
なお、existsの場合はアキュムレーターが不要なので、「左から再帰」でも「基底値定義の埋め込み」ができます。
そうなるともう完全に「左から再帰」で書いた方が綺麗です。

まとめ

要件	「右から再帰」	「左から再帰」	備考
最左値取得	×	○
最右値取得	○	×
分かりやすい	○	×	人による？
基底値定義埋込	○	×	アキュムレーターが不要なら無関係
末尾再帰	×	○
メモ化	○	×
呼出動的キャンセル	×	○

（注：×は「できない」というよりは「相対的に良くない」的なカンジです。）

おわり。