1. きっかけ
年始にM3マック買った。うれしくてmlx_lmを使って推論した。↓
そしたら、学習したくなった。ただそれだけだ!w
2. 自分のMacと環境
MacBookAir(2025年1月初売りで購入)
CPU:M3
ユニファイドメモリー:24GB
SSD:1T
バージョン関連
Python==3.11.8
mlx_lm==0.21.1
3. 公式
基本的にmlx_lmのGitHubを見て実行している。Qiita様にも記事が少ないしね!きっとこれはみんなの役に立つ。
4. 学習の準備
ザクっとここに書いてある。が、わかりにくいので整理する。
- データの用意
- 学習方法を選択
- パラメータ設定
- 学習
よし、こんな手順でいこう。
4-1 学習データの用意
基本的にここに書いてある。
が、わかりにくい。
僕が用意したのはこんな形式のjsonl
これをtrain_dataフォルダにtrain.jsonl、eval.jsonl、test.jsonlとして入れておこう。これらはkan_hatakeyamaさんのデータセットから抜粋して加工させていただいた。
train.jsonl
[{"text": "### 指示\nあなたが長方形の庭を持っていると想像してください。その庭は幅が10メートル、奥行きが5メートルあります。花を植えることに決めましたが、庭の周囲に沿って植えます。もし4人の友達があなたを手伝って花を咲かせるなら、それぞれの人が庭の隅から始めて次の角に向かって歩く場合、全員が同時に作業を終え、仕事を均等に分けると各人がどれくらいの距離を歩くことになるでしょうか?\n### 回答\n友達が歩く距離を計算するためには、まず庭の総周長を求める必要があります。この庭は長さが10メートルで幅が5メートルの長方形なので、長方形の面積の公式を使って周長(P)を以下のように計算します:\n\n\\( P = 2 \\times (長さ+幅) \\)\n\nこれを具体的な数値に当てはめると:\n\n\\( P = 2 \\times (10m + 5m) \\) \n\\( P = 2 \\times 15m \\) \n\\( P = 30m \\)\n\n次に、四人の友達が花を植えるためにそれぞれ異なる角から始めて次の角に向かって進むとします。この場合、各友人は長方形の一辺に沿って花を咲かせる責任を負います。\n\n長方形には長い側面が二つあり、それぞれが10メートルの長さを持ちます。また短い側面も二つあり、それぞれが5メートルの長さを持っています。もし各友人がちょうど一辺を歩く場合を考えると、二人の友人が10メートルずつ歩き、残り二人が5メートルずつ歩くことになります。しかしこれでは作業が均等に分配されません。なぜなら全体の距離は均等に配分されないからです。\n\n作業を公平に分割するために、各友人の歩く距離は等しいべきです。総周長が30メートルであることを考えると、各友人はこの周長の1/4を歩きます。したがって次のように計算できます:\n\n一人当たりの距離 = 総周長 ÷ 人数 \n1人あたりの距離 = 30m ÷ 4人 \n1人あたりの距離 = 7.5m\n\nつまり、各友人が同じ距離を歩いて同時に作業を終えるようにするには、各友人が角から始まり次の角まで進み、7.5メートル歩く必要があります。これは一人が約半分の短い側またはほぼ半分の長い側のどちらかの端をカバーすることを意味します。</s>"}
{"text": "### 指示\nグリッドマップ上で、以下の位置に四つの市がマークされています:City Aは座標(2, 3)、City Bは座標(4, 5)、City Cは座標(6, 7)にあり、そしてCity Dは座標(8, 9)にあります。各市には固有のシンボルが付いており、それは星、円、三角形、四角形です。これらの座標のパターンを調べることで、どの形がCity Dに対応するかを特定できますか?\n### 回答\nCity Dに対応する形状を特定するために、まず提供された都市の座標パターンを確認しましょう:\n\n- City Aは座標(2,3)にあります。\n- City Bは座標(4,5)にあります。\n- City Cは座標(6,7)にあります。\n- City Dは座標(8,9)にあります。\n\n各都市のx軸(水平)およびy軸(垂直)に沿った座標が2ずつ増加していることがわかります。これは、もし形状と都市の対応関係が座標に基づくパターンであるならば、そのパターンは位置の順序か実際の数値値に関連する可能性があることを意味します。\n\n形状をどのように都市に対応させるのかについての情報がないため、我々はただ推測するしかありません。ただし、他のすべての都市が言及されている中で、City Dが最も最後にあるため、単純なアプローチとして都市名をアルファベット順に並べたり、他の秩序で形状を割り当てることが考えられます。\n\n例えば、都市の名前をアルファベット順に基づいて形状を割り当てる場合、以下のようなシーケンスが考えられます:\n\n- City A(アルファベット順の最初)-星形\n- City B(次に来るもの)-円\n- City C(その次)-三角形\n- City D(最後に来るもの)-四角形\n\nこのパターンに従うと、City Dは四角形に該当することが分かります。\n\nまた、形状が座標の増加数値に基づいている可能性もあります。この場合も、同様の結果になるかもしれません:\n\n- City A(最も低い座標)-星型\n- City B(次に低い座標)-円形\n- City C(次に高い座標)-三角形\n- City D(最も高い座標)-正方形\n\nここでも同様に、City Dは正方形に該当するでしょう。\n\n追加の形状と都市の関連情報がない限り、これらの推測は合理的です。したがって、観察したパターンや反対情報が不足していることから、City Dはおそらく正方形であると結論付けることができます。</s>"}
{"text": "### 指示\n質問1:6人家族において、各兄弟姉妹のペアの年齢差がちょうど3歳である2組の兄弟がいます。最年少のペアの合計年齢が24歳で、最年長のペアの合計年齢は最年少のペアの倍であるとします。この家族の子供たち全員の年齢はいくつですか?\n\n質問2:以下の非グラムパズルの手掛かりに基づいて、5×5グリッドを埋めてください。これにより家族のポートレートが明らかになります。\n\n1行目:1 1 \n2行目:2 2 \n3行目:1 1 1 \n4行目:2 1 1 \n5行目:1 1 1 1 1 \n\n1列目:1 1 1 1 1 \n2列目:2 2 1 1 \n3列目:1 1 2 2 \n4列目:1 1 2 1 \n5列目:1 1 1 1\n### 回答\n### Question 1:\n\n1. 最年少のペアの年齢を \\( A \\) と \\( B \\) で表します。ここで、\\( A \\) は年少の子供の年齢で、\\( B \\) は年長の子供の年齢です。私たちは次の情報を知っています:\n - \\( A + B = 24 \\)(方程式1)\n\n また、各兄弟姉妹の間に年齢差がちょうど3歳あるため、次のように言えます:\n \n - \\( B = A + 3 \\)(方程式2)\n\n 今、方程式2を方程式1に代入してみましょう:\n\n \\( A + (A + 3) = 24 \\)\n \n この結果から、\n\n \\( 2A + 3 = 24 \\)\n \n 2つの方程式を解くと、\n \n \\( 2A = 21 \\) \n \\( A = 10.5 \\)\n \n したがって、最年少の子供は10.5歳で、方程式2を使って年長の子供の年齢を求めると、\n \n \\( B = A + 3 \\)\n \\( B = 10.5 + 3 \\)\n \\( B = 13.5 \\)\n \n 最年長のペアの合計年齢は、最年少のペアの年齢のちょうど2倍であることがわかります。もし彼らの年齢をそれぞれ \\( C \\) および \\( D \\) (\\( C \\) が年少で \\( D \\) が年長)とすると、\n \n \\( C + D = 2 \\times (A + B) \\)\n \\( C + D = 2 \\times 24 \\)\n \\( C + D = 48 \\)\n \n そして、このペアにも3歳の差があるため、\n \n \\( D = C + 3 \\)\n \n この等式を前の式に代入すると、\n \n \\( C + (C + 3) = 48 \\)\n \n これは次のように解けます:\n \n \\( 2C + 3 = 48 \\)\n \\( 2C = 45 \\)\n \\( C = 22.5 \\)\n \n 年長の兄弟姉妹の年下の人物は22.5歳であり、差分方程式を使うと、\n \n \\( D = C + 3 \\)\n \\( D = 22.5 + 3 \\)\n \\( D = 25.5 \\)\n \n よって、子供たちの年齢は次のようになります:\n - 最年少のペア:10.5歳と13.5歳\n - 年長のペア:22.5歳と25.5歳\n\n### Question 2:\n\nこの数独パズルを解くためには、与えられたヒントに基づいてどのセルを埋めるべきかを決定する必要があります。行と列を順番に確認していきましょう:\n\n#### 行1:\n行の最初には2つのブロックが別々にありますが、列1には連続した5個の「1」が存在するため、これらは同じブロックの一部でなければなりません。そのため、最初のセルを行1に埋めます。\n\n#### 行2:\n行2には2つのブロックがあり、列2の上部には2つの「2」があります。このため、最初に行2の最初の2つのセルは埋められます。第二のブロックは同じ列に配置できないので、第2ブロックは列4および5に位置しなければなりません。\n\n#### 行3:\n行3には3つの独立したブロックが1つあります。すでに列1によって最初のセルが埋まっていることはわかっています。次のブロックは列2または3に置くことができません(既に「2」がある)。これは列4に続くもう一つのブロックとして配置されます。\n\n#### 行4:\n行4には2つの「1」、続いて1つの「2」が続きます。最初のセルは既に列1により決定されています。「1」の次のセルは行2に基づき列2にあり、「1」の後にもう一つ「1」が行3にある必要があります。最後のブロック「2」は列4および5にあります。\n\n#### 行5:\nすべてのセルはすでに提供されたヒント「1 1 1 1 1」に従って埋められています。\n\n#### 列1:\nすべての列も「1 1 1 1 1」のヒントに従います。\n\n#### 列2:\n上部に2つの「2」が存在し、それらはすでに行1および行2で満たされていることを確認しました。残りの行は単一の「1」により自動的に満たされます。\n\n#### 列3:\n最下部の2つの「2」について知っており、それらも行4および5で満たされるべきです。トップ2つのセルは空のまま残ります(「1」の行1および行2による制約のため)。\n\n#### 列4:\n最上部の「2」は行1および行2で満たされており、第三の位置は既に行3により決定されています。第四の位置は空白のままとなります(「1」の行4による制約のため)。\n\n#### 列5:\nすべてのセルは前述のヒントに従い、行2、3、および4からの要求を満たしています。\n\n最終的に、すべてのセルを埋めた後の完成形は次のようになるはずです:\n\n```\nX O O O\nX X O O\nO O X X\nO O X O\nX X X X X\n```\n\nここで、\"X\"は塗りつぶされたセルを示し、\"O\"は空のセルを示します。これにより、単純な家族の肖像画が表示され、両親と子供たちの絵が明らかになるでしょう。</s>"}]
eval.jsonl
[{"text": "### 指示\nあなたが長方形の庭を持っていると想像してください。その庭は幅が10メートル、奥行きが5メートルあります。花を植えることに決めましたが、庭の周囲に沿って植えます。もし4人の友達があなたを手伝って花を咲かせるなら、それぞれの人が庭の隅から始めて次の角に向かって歩く場合、全員が同時に作業を終え、仕事を均等に分けると各人がどれくらいの距離を歩くことになるでしょうか?\n### 回答\n友達が歩く距離を計算するためには、まず庭の総周長を求める必要があります。この庭は長さが10メートルで幅が5メートルの長方形なので、長方形の面積の公式を使って周長(P)を以下のように計算します:\n\n\\( P = 2 \\times (長さ+幅) \\)\n\nこれを具体的な数値に当てはめると:\n\n\\( P = 2 \\times (10m + 5m) \\) \n\\( P = 2 \\times 15m \\) \n\\( P = 30m \\)\n\n次に、四人の友達が花を植えるためにそれぞれ異なる角から始めて次の角に向かって進むとします。この場合、各友人は長方形の一辺に沿って花を咲かせる責任を負います。\n\n長方形には長い側面が二つあり、それぞれが10メートルの長さを持ちます。また短い側面も二つあり、それぞれが5メートルの長さを持っています。もし各友人がちょうど一辺を歩く場合を考えると、二人の友人が10メートルずつ歩き、残り二人が5メートルずつ歩くことになります。しかしこれでは作業が均等に分配されません。なぜなら全体の距離は均等に配分されないからです。\n\n作業を公平に分割するために、各友人の歩く距離は等しいべきです。総周長が30メートルであることを考えると、各友人はこの周長の1/4を歩きます。したがって次のように計算できます:\n\n一人当たりの距離 = 総周長 ÷ 人数 \n1人あたりの距離 = 30m ÷ 4人 \n1人あたりの距離 = 7.5m\n\nつまり、各友人が同じ距離を歩いて同時に作業を終えるようにするには、各友人が角から始まり次の角まで進み、7.5メートル歩く必要があります。これは一人が約半分の短い側またはほぼ半分の長い側のどちらかの端をカバーすることを意味します。</s>"}
{"text": "### 指示\nグリッドマップ上で、以下の位置に四つの市がマークされています:City Aは座標(2, 3)、City Bは座標(4, 5)、City Cは座標(6, 7)にあり、そしてCity Dは座標(8, 9)にあります。各市には固有のシンボルが付いており、それは星、円、三角形、四角形です。これらの座標のパターンを調べることで、どの形がCity Dに対応するかを特定できますか?\n### 回答\nCity Dに対応する形状を特定するために、まず提供された都市の座標パターンを確認しましょう:\n\n- City Aは座標(2,3)にあります。\n- City Bは座標(4,5)にあります。\n- City Cは座標(6,7)にあります。\n- City Dは座標(8,9)にあります。\n\n各都市のx軸(水平)およびy軸(垂直)に沿った座標が2ずつ増加していることがわかります。これは、もし形状と都市の対応関係が座標に基づくパターンであるならば、そのパターンは位置の順序か実際の数値値に関連する可能性があることを意味します。\n\n形状をどのように都市に対応させるのかについての情報がないため、我々はただ推測するしかありません。ただし、他のすべての都市が言及されている中で、City Dが最も最後にあるため、単純なアプローチとして都市名をアルファベット順に並べたり、他の秩序で形状を割り当てることが考えられます。\n\n例えば、都市の名前をアルファベット順に基づいて形状を割り当てる場合、以下のようなシーケンスが考えられます:\n\n- City A(アルファベット順の最初)-星形\n- City B(次に来るもの)-円\n- City C(その次)-三角形\n- City D(最後に来るもの)-四角形\n\nこのパターンに従うと、City Dは四角形に該当することが分かります。\n\nまた、形状が座標の増加数値に基づいている可能性もあります。この場合も、同様の結果になるかもしれません:\n\n- City A(最も低い座標)-星型\n- City B(次に低い座標)-円形\n- City C(次に高い座標)-三角形\n- City D(最も高い座標)-正方形\n\nここでも同様に、City Dは正方形に該当するでしょう。\n\n追加の形状と都市の関連情報がない限り、これらの推測は合理的です。したがって、観察したパターンや反対情報が不足していることから、City Dはおそらく正方形であると結論付けることができます。</s>"}
{"text": "### 指示\n質問1:6人家族において、各兄弟姉妹のペアの年齢差がちょうど3歳である2組の兄弟がいます。最年少のペアの合計年齢が24歳で、最年長のペアの合計年齢は最年少のペアの倍であるとします。この家族の子供たち全員の年齢はいくつですか?\n\n質問2:以下の非グラムパズルの手掛かりに基づいて、5×5グリッドを埋めてください。これにより家族のポートレートが明らかになります。\n\n1行目:1 1 \n2行目:2 2 \n3行目:1 1 1 \n4行目:2 1 1 \n5行目:1 1 1 1 1 \n\n1列目:1 1 1 1 1 \n2列目:2 2 1 1 \n3列目:1 1 2 2 \n4列目:1 1 2 1 \n5列目:1 1 1 1\n### 回答\n### Question 1:\n\n1. 最年少のペアの年齢を \\( A \\) と \\( B \\) で表します。ここで、\\( A \\) は年少の子供の年齢で、\\( B \\) は年長の子供の年齢です。私たちは次の情報を知っています:\n - \\( A + B = 24 \\)(方程式1)\n\n また、各兄弟姉妹の間に年齢差がちょうど3歳あるため、次のように言えます:\n \n - \\( B = A + 3 \\)(方程式2)\n\n 今、方程式2を方程式1に代入してみましょう:\n\n \\( A + (A + 3) = 24 \\)\n \n この結果から、\n\n \\( 2A + 3 = 24 \\)\n \n 2つの方程式を解くと、\n \n \\( 2A = 21 \\) \n \\( A = 10.5 \\)\n \n したがって、最年少の子供は10.5歳で、方程式2を使って年長の子供の年齢を求めると、\n \n \\( B = A + 3 \\)\n \\( B = 10.5 + 3 \\)\n \\( B = 13.5 \\)\n \n 最年長のペアの合計年齢は、最年少のペアの年齢のちょうど2倍であることがわかります。もし彼らの年齢をそれぞれ \\( C \\) および \\( D \\) (\\( C \\) が年少で \\( D \\) が年長)とすると、\n \n \\( C + D = 2 \\times (A + B) \\)\n \\( C + D = 2 \\times 24 \\)\n \\( C + D = 48 \\)\n \n そして、このペアにも3歳の差があるため、\n \n \\( D = C + 3 \\)\n \n この等式を前の式に代入すると、\n \n \\( C + (C + 3) = 48 \\)\n \n これは次のように解けます:\n \n \\( 2C + 3 = 48 \\)\n \\( 2C = 45 \\)\n \\( C = 22.5 \\)\n \n 年長の兄弟姉妹の年下の人物は22.5歳であり、差分方程式を使うと、\n \n \\( D = C + 3 \\)\n \\( D = 22.5 + 3 \\)\n \\( D = 25.5 \\)\n \n よって、子供たちの年齢は次のようになります:\n - 最年少のペア:10.5歳と13.5歳\n - 年長のペア:22.5歳と25.5歳\n\n### Question 2:\n\nこの数独パズルを解くためには、与えられたヒントに基づいてどのセルを埋めるべきかを決定する必要があります。行と列を順番に確認していきましょう:\n\n#### 行1:\n行の最初には2つのブロックが別々にありますが、列1には連続した5個の「1」が存在するため、これらは同じブロックの一部でなければなりません。そのため、最初のセルを行1に埋めます。\n\n#### 行2:\n行2には2つのブロックがあり、列2の上部には2つの「2」があります。このため、最初に行2の最初の2つのセルは埋められます。第二のブロックは同じ列に配置できないので、第2ブロックは列4および5に位置しなければなりません。\n\n#### 行3:\n行3には3つの独立したブロックが1つあります。すでに列1によって最初のセルが埋まっていることはわかっています。次のブロックは列2または3に置くことができません(既に「2」がある)。これは列4に続くもう一つのブロックとして配置されます。\n\n#### 行4:\n行4には2つの「1」、続いて1つの「2」が続きます。最初のセルは既に列1により決定されています。「1」の次のセルは行2に基づき列2にあり、「1」の後にもう一つ「1」が行3にある必要があります。最後のブロック「2」は列4および5にあります。\n\n#### 行5:\nすべてのセルはすでに提供されたヒント「1 1 1 1 1」に従って埋められています。\n\n#### 列1:\nすべての列も「1 1 1 1 1」のヒントに従います。\n\n#### 列2:\n上部に2つの「2」が存在し、それらはすでに行1および行2で満たされていることを確認しました。残りの行は単一の「1」により自動的に満たされます。\n\n#### 列3:\n最下部の2つの「2」について知っており、それらも行4および5で満たされるべきです。トップ2つのセルは空のまま残ります(「1」の行1および行2による制約のため)。\n\n#### 列4:\n最上部の「2」は行1および行2で満たされており、第三の位置は既に行3により決定されています。第四の位置は空白のままとなります(「1」の行4による制約のため)。\n\n#### 列5:\nすべてのセルは前述のヒントに従い、行2、3、および4からの要求を満たしています。\n\n最終的に、すべてのセルを埋めた後の完成形は次のようになるはずです:\n\n```\nX O O O\nX X O O\nO O X X\nO O X O\nX X X X X\n```\n\nここで、\"X\"は塗りつぶされたセルを示し、\"O\"は空のセルを示します。これにより、単純な家族の肖像画が表示され、両親と子供たちの絵が明らかになるでしょう。</s>"}]
test.jsonl
[{"text": "### 指示\nあなたが長方形の庭を持っていると想像してください。その庭は幅が10メートル、奥行きが5メートルあります。花を植えることに決めましたが、庭の周囲に沿って植えます。もし4人の友達があなたを手伝って花を咲かせるなら、それぞれの人が庭の隅から始めて次の角に向かって歩く場合、全員が同時に作業を終え、仕事を均等に分けると各人がどれくらいの距離を歩くことになるでしょうか?\n### 回答\n友達が歩く距離を計算するためには、まず庭の総周長を求める必要があります。この庭は長さが10メートルで幅が5メートルの長方形なので、長方形の面積の公式を使って周長(P)を以下のように計算します:\n\n\\( P = 2 \\times (長さ+幅) \\)\n\nこれを具体的な数値に当てはめると:\n\n\\( P = 2 \\times (10m + 5m) \\) \n\\( P = 2 \\times 15m \\) \n\\( P = 30m \\)\n\n次に、四人の友達が花を植えるためにそれぞれ異なる角から始めて次の角に向かって進むとします。この場合、各友人は長方形の一辺に沿って花を咲かせる責任を負います。\n\n長方形には長い側面が二つあり、それぞれが10メートルの長さを持ちます。また短い側面も二つあり、それぞれが5メートルの長さを持っています。もし各友人がちょうど一辺を歩く場合を考えると、二人の友人が10メートルずつ歩き、残り二人が5メートルずつ歩くことになります。しかしこれでは作業が均等に分配されません。なぜなら全体の距離は均等に配分されないからです。\n\n作業を公平に分割するために、各友人の歩く距離は等しいべきです。総周長が30メートルであることを考えると、各友人はこの周長の1/4を歩きます。したがって次のように計算できます:\n\n一人当たりの距離 = 総周長 ÷ 人数 \n1人あたりの距離 = 30m ÷ 4人 \n1人あたりの距離 = 7.5m\n\nつまり、各友人が同じ距離を歩いて同時に作業を終えるようにするには、各友人が角から始まり次の角まで進み、7.5メートル歩く必要があります。これは一人が約半分の短い側またはほぼ半分の長い側のどちらかの端をカバーすることを意味します。</s>"}
{"text": "### 指示\nグリッドマップ上で、以下の位置に四つの市がマークされています:City Aは座標(2, 3)、City Bは座標(4, 5)、City Cは座標(6, 7)にあり、そしてCity Dは座標(8, 9)にあります。各市には固有のシンボルが付いており、それは星、円、三角形、四角形です。これらの座標のパターンを調べることで、どの形がCity Dに対応するかを特定できますか?\n### 回答\nCity Dに対応する形状を特定するために、まず提供された都市の座標パターンを確認しましょう:\n\n- City Aは座標(2,3)にあります。\n- City Bは座標(4,5)にあります。\n- City Cは座標(6,7)にあります。\n- City Dは座標(8,9)にあります。\n\n各都市のx軸(水平)およびy軸(垂直)に沿った座標が2ずつ増加していることがわかります。これは、もし形状と都市の対応関係が座標に基づくパターンであるならば、そのパターンは位置の順序か実際の数値値に関連する可能性があることを意味します。\n\n形状をどのように都市に対応させるのかについての情報がないため、我々はただ推測するしかありません。ただし、他のすべての都市が言及されている中で、City Dが最も最後にあるため、単純なアプローチとして都市名をアルファベット順に並べたり、他の秩序で形状を割り当てることが考えられます。\n\n例えば、都市の名前をアルファベット順に基づいて形状を割り当てる場合、以下のようなシーケンスが考えられます:\n\n- City A(アルファベット順の最初)-星形\n- City B(次に来るもの)-円\n- City C(その次)-三角形\n- City D(最後に来るもの)-四角形\n\nこのパターンに従うと、City Dは四角形に該当することが分かります。\n\nまた、形状が座標の増加数値に基づいている可能性もあります。この場合も、同様の結果になるかもしれません:\n\n- City A(最も低い座標)-星型\n- City B(次に低い座標)-円形\n- City C(次に高い座標)-三角形\n- City D(最も高い座標)-正方形\n\nここでも同様に、City Dは正方形に該当するでしょう。\n\n追加の形状と都市の関連情報がない限り、これらの推測は合理的です。したがって、観察したパターンや反対情報が不足していることから、City Dはおそらく正方形であると結論付けることができます。</s>"}
{"text": "### 指示\n質問1:6人家族において、各兄弟姉妹のペアの年齢差がちょうど3歳である2組の兄弟がいます。最年少のペアの合計年齢が24歳で、最年長のペアの合計年齢は最年少のペアの倍であるとします。この家族の子供たち全員の年齢はいくつですか?\n\n質問2:以下の非グラムパズルの手掛かりに基づいて、5×5グリッドを埋めてください。これにより家族のポートレートが明らかになります。\n\n1行目:1 1 \n2行目:2 2 \n3行目:1 1 1 \n4行目:2 1 1 \n5行目:1 1 1 1 1 \n\n1列目:1 1 1 1 1 \n2列目:2 2 1 1 \n3列目:1 1 2 2 \n4列目:1 1 2 1 \n5列目:1 1 1 1\n### 回答\n### Question 1:\n\n1. 最年少のペアの年齢を \\( A \\) と \\( B \\) で表します。ここで、\\( A \\) は年少の子供の年齢で、\\( B \\) は年長の子供の年齢です。私たちは次の情報を知っています:\n - \\( A + B = 24 \\)(方程式1)\n\n また、各兄弟姉妹の間に年齢差がちょうど3歳あるため、次のように言えます:\n \n - \\( B = A + 3 \\)(方程式2)\n\n 今、方程式2を方程式1に代入してみましょう:\n\n \\( A + (A + 3) = 24 \\)\n \n この結果から、\n\n \\( 2A + 3 = 24 \\)\n \n 2つの方程式を解くと、\n \n \\( 2A = 21 \\) \n \\( A = 10.5 \\)\n \n したがって、最年少の子供は10.5歳で、方程式2を使って年長の子供の年齢を求めると、\n \n \\( B = A + 3 \\)\n \\( B = 10.5 + 3 \\)\n \\( B = 13.5 \\)\n \n 最年長のペアの合計年齢は、最年少のペアの年齢のちょうど2倍であることがわかります。もし彼らの年齢をそれぞれ \\( C \\) および \\( D \\) (\\( C \\) が年少で \\( D \\) が年長)とすると、\n \n \\( C + D = 2 \\times (A + B) \\)\n \\( C + D = 2 \\times 24 \\)\n \\( C + D = 48 \\)\n \n そして、このペアにも3歳の差があるため、\n \n \\( D = C + 3 \\)\n \n この等式を前の式に代入すると、\n \n \\( C + (C + 3) = 48 \\)\n \n これは次のように解けます:\n \n \\( 2C + 3 = 48 \\)\n \\( 2C = 45 \\)\n \\( C = 22.5 \\)\n \n 年長の兄弟姉妹の年下の人物は22.5歳であり、差分方程式を使うと、\n \n \\( D = C + 3 \\)\n \\( D = 22.5 + 3 \\)\n \\( D = 25.5 \\)\n \n よって、子供たちの年齢は次のようになります:\n - 最年少のペア:10.5歳と13.5歳\n - 年長のペア:22.5歳と25.5歳\n\n### Question 2:\n\nこの数独パズルを解くためには、与えられたヒントに基づいてどのセルを埋めるべきかを決定する必要があります。行と列を順番に確認していきましょう:\n\n#### 行1:\n行の最初には2つのブロックが別々にありますが、列1には連続した5個の「1」が存在するため、これらは同じブロックの一部でなければなりません。そのため、最初のセルを行1に埋めます。\n\n#### 行2:\n行2には2つのブロックがあり、列2の上部には2つの「2」があります。このため、最初に行2の最初の2つのセルは埋められます。第二のブロックは同じ列に配置できないので、第2ブロックは列4および5に位置しなければなりません。\n\n#### 行3:\n行3には3つの独立したブロックが1つあります。すでに列1によって最初のセルが埋まっていることはわかっています。次のブロックは列2または3に置くことができません(既に「2」がある)。これは列4に続くもう一つのブロックとして配置されます。\n\n#### 行4:\n行4には2つの「1」、続いて1つの「2」が続きます。最初のセルは既に列1により決定されています。「1」の次のセルは行2に基づき列2にあり、「1」の後にもう一つ「1」が行3にある必要があります。最後のブロック「2」は列4および5にあります。\n\n#### 行5:\nすべてのセルはすでに提供されたヒント「1 1 1 1 1」に従って埋められています。\n\n#### 列1:\nすべての列も「1 1 1 1 1」のヒントに従います。\n\n#### 列2:\n上部に2つの「2」が存在し、それらはすでに行1および行2で満たされていることを確認しました。残りの行は単一の「1」により自動的に満たされます。\n\n#### 列3:\n最下部の2つの「2」について知っており、それらも行4および5で満たされるべきです。トップ2つのセルは空のまま残ります(「1」の行1および行2による制約のため)。\n\n#### 列4:\n最上部の「2」は行1および行2で満たされており、第三の位置は既に行3により決定されています。第四の位置は空白のままとなります(「1」の行4による制約のため)。\n\n#### 列5:\nすべてのセルは前述のヒントに従い、行2、3、および4からの要求を満たしています。\n\n最終的に、すべてのセルを埋めた後の完成形は次のようになるはずです:\n\n```\nX O O O\nX X O O\nO O X X\nO O X O\nX X X X X\n```\n\nここで、\"X\"は塗りつぶされたセルを示し、\"O\"は空のセルを示します。これにより、単純な家族の肖像画が表示され、両親と子供たちの絵が明らかになるでしょう。</s>"}]
ここは手抜きなのでデータの中身は全部同じだけど、三つファイルが必要であることはお忘れなく。DeepLearningをしている人ならそれぞれの役割はわかると思う。真面目にやるならちゃんとデータを作ろう。
4-2 学習手法の選択
GitHubにはLoRAの説明があるのでLoRAで学習してみよう。
LoRAは別途ググってください。ヲイ
4-3 パラメータの設定
パラメータの確認方法
GitHubを探っていくと何となくパラメータの種類がわかる。
先のLORA.mdを見てみると直接lora.pyを呼んでいるようなので、mlx_lm直下のlora.pyを見てみる
ここにハイパラが設定されそうだ。
しかし、ちょっと待て。学習させる層を決めるのはどこだ?
ちょっとここで冷静になる。たしか、コマンドラインでの学習時に設定を渡す方法は二つある。
- それぞれの設定を引数として渡す方法
- 設定のyamlファイルを用意し、このファイルを引数として渡す方法
ということで、yamlファイルのサンプルを見に行ってみる
あった。
lora_parameters:
# The layer keys to apply LoRA to.
# These will be applied for the last lora_layers
keys: ["self_attn.q_proj", "self_attn.v_proj"]
rank: 8
scale: 20.0
dropout: 0.0
なるほど。lora_parametersに辞書形式で渡せば良さそうだ。
あと、yamlファイルを作っておいた方が、確かに管理しやすいかもしれない。次回以降に検討しよう。
これはyamlファイルで渡さないとできないっぽい。
lora.pyのargparseに受取先がない。ということで、今回はあきらめる(あっさり)。
4-4 学習時のコマンドを考えてみる
mlx_lm.lora \
--model <モデルのレポジトリか、ダウンロードしたモデルのパス> \ # 学習させるモデル
--train \ # 学習フラグ
--data train_data \ # 学習データへのパスこのパスの中に三つのファイルがある
--adapter-path adapter_cli \ # LoRAモデルを保存するパス
--iters 5 # 学習回数(エポック数)
--max-seq-length 1024 \ # 出力データ長
--steps-per-report 1 \ # 学習の実行状況を何ステップごとに表示するか
--val-batches 2 \ # 評価時のバッチ数(高いとMacが固まる)
--test-batches 2 \ # テスト時のバッチ数(高いとMacが固まる)
こんな感じにしてみた。解説は中に書いておいたのでよろぴこ。
4-5 メモリー問題への対処
僕のMacBookAirも24GBしかないのでメモリーが足りなくなる。
対策方法はここに書いてある。僕も4bit量子化し、さらに学習する層を目的に合わせて特定の層だけにしている。
from mlx_lm import convert
convert(
hf_path = hf_repo,
mlx_path = mlx_path,
dtype="bfloat16",
quantize=True, # 量子化設定
q_bits=8 # 8bitを指定。
)
quantizeをTrueにして、q_bitsを8とか、4に指定すれば随分とメモリーを削減できると思う。精度も落ちるけどね。
量子化していても、バッチ数が大きいとMacが固まることもありました。w
unslothのようにGradient Accumulation機能があるといいなぁ。
5. 学習
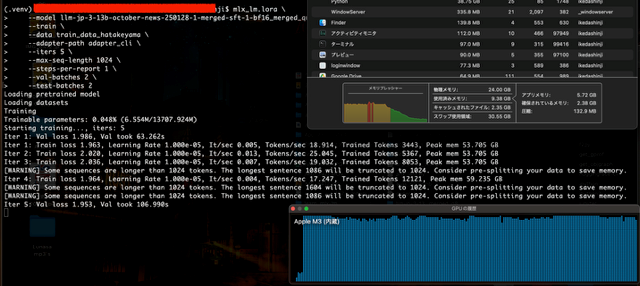
と言うことで実行してみた。
めっちゃメモリー食ってるけど、スワップしてメモリーを逃がしてる。
きっとバックプロパゲーションの時に60GB近くのメモリーを食ってくるんじゃないかな。
でもユニファイドメモリーのおかげで、メモリーをうまく処理してくれるので何とか計算できています。きっと速度はめっちゃ遅い。やっぱり学習する層を指定しないとなぁ。デフォルト設定がわからんし。

そして、最後
最終のエポックが終わってから何かしら処理してます。
コマンドラインが戻ってくるまでひたすら待ちです。
6. 学習結果
確認しようとしたら学習したモデルがインストラクションチューニング済みだったので、差がわからんというオチ。
お見せできず、ごめんなさい。
今度はNotebook形式でやってみるのでリベンジします。
7. おわりに
mlx_lmのGitHubを見ていて思ったんだけど、mlx_lmってtransformersライブラリのラッパーみたいな感じなんですね。いたるところで、transformersのクラスが出てきます。だから使い方が似てます。
なので、transformers + GoogleColabで慣れて、そのあとにmlx_lmを触れば理解がはやいのかもしれません。また、LoRAを使うなら、unslothをGoogleColabで使ってみるとすごくわかりやすい。サンプルも多いですし。
なんていったってmlx_lmは情報が少なすぎる
以前、あっさり挫折したmlx_lmですが、今回は学習までこぎつけることができました。自分のプログラムを読む力が向上したのかもしれませんが、事前の知識習得があったからというのが一番大きい。松尾・岩澤研の大規模言語モデル2024はマジで神講座だと思います。そのおかげで、今回は新しく理解する範囲が少なくて済んだんだと思います。少しずつステップ踏めば僕たちもツヨツヨエンジニアになれるのかもしれません。
次はコマンドラインではなくて、ノートブック形式でやっちゃおう。
今度こそ、 インストラクションチューニングしていないモデル で、 学習する層を指定 してやってみたいと思います。この宣言は守られるのか!?。
ではまた