今年もAdvent Calendarの季節ですね。ZabbixのAdvent Calendarの初日担当させていただきます。
全然枠埋まってないので皆さんぜひ!
初回は、Zabbixで監視したデータから、少し統計的な情報を取り出してみようというテーマです。
Zabbixは、監視したデータに対して四則演算したり、トリガー関数という形で計算処理できる機能が提供されていたりします。これらを使って生の監視データからどういった加工ができるのかをチャレンジしてみます。(結構無理やりなところがあるので、本当にやりたいならZabbixからデータを取り出してZabbix以外の分析が得意なツールとかにおまかせするのが良いと思いますが。。)
算出できるか試した値
- 単純移動平均値(Wikipedia)
- 単純に特定の期間の監視データの平均値を算出
- 使いみち
- 監視データの平滑化
- 次点の予測値として活用
- 加重移動平均値(Wikipedia)
- 特定の期間の監視データに対して、直近のデータに特に重みを多くつけつ、古いデータに重みを低めにつけて平均値を算出
- 使いみち
- 監視データの平滑化
- 直近の値に重みをつけた平均値を次点の予測値として活用
- 指数平滑移動平均値(Wikipedia)
- 特定の期間の監視データの平均に対して、一定の係数を掛けた値を順次計算して求める平均値
- 使いみち
- 監視データの平滑化。
- 加重移動平均・単純移動平均は特定の期間のデータのみを含んだ平均値となるが、指数平滑移動平均は常に前回の平均値に対する掛け算をして次の値を求めていくために過去の傾向をすべて反映した次点の予測値を算出
- 中央値(Wikipedia)
- 特定の期間の監視データの中で上位50%の位置にくる値
- 使いみち
- 監視データに大小の偏りがある場合に見ると役立つかもしれない代表値
- 自己相関係数(Wikipedia)
- 時系列の監視データが過去の時間と相関関係がどのぐらいあるかの値
- 使いみち
- 過去の監視データが未来の監視結果を予測するために活用できるかを判断するための指標
- 監視データがどういう周期性を持っているかを確認するのに有効
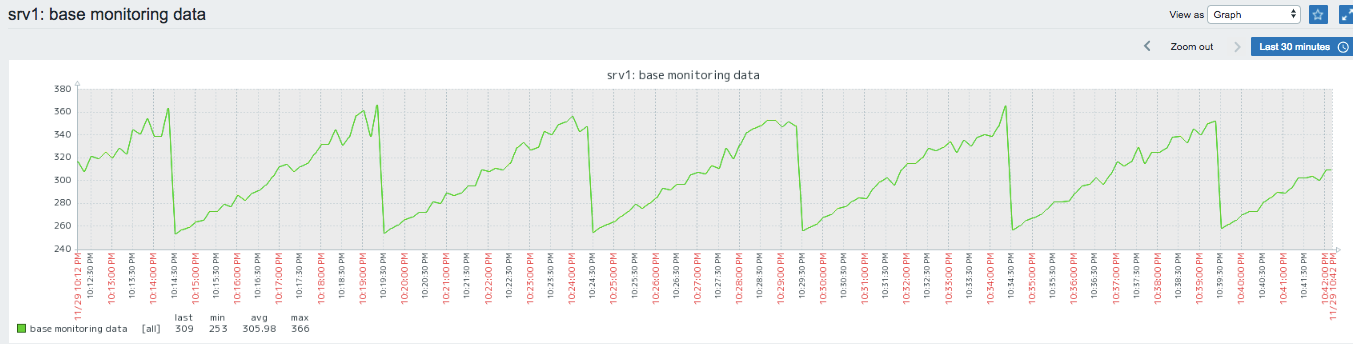
統計値を算出する元のデータ系列
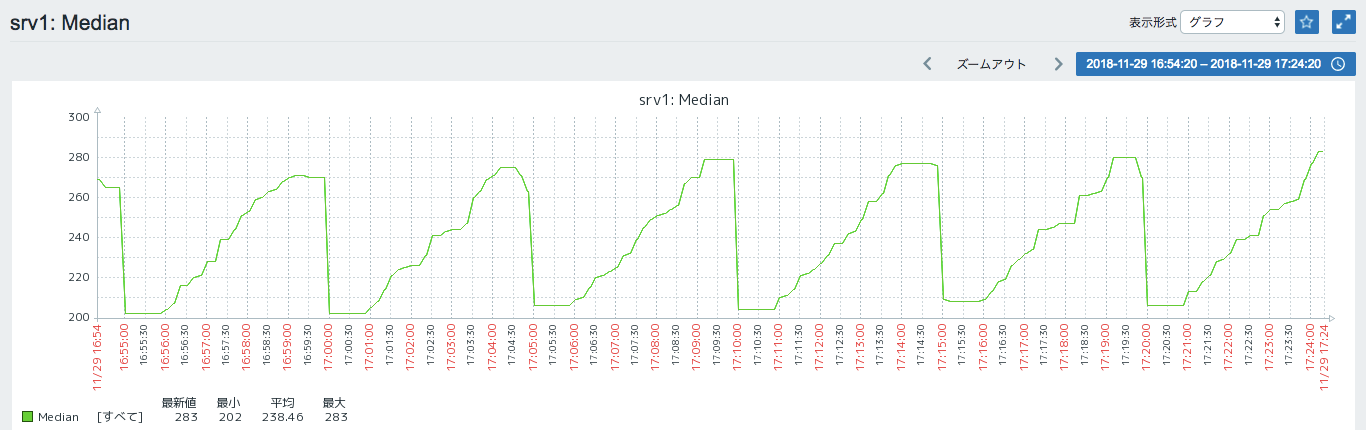
今回は擬似的にこんなデータを用意。
単純移動平均
計算式
tの時点における直近n個の監視データ(x)の単純移動平均値yの式
y_t = \frac{x_t+x_{t-1}+x_{t-2}+\cdots+x_{t-n}}{n}
算出の方針
トリガー関数のavgを利用し、直近x件の監視データの平均値を算出する計算アイテムを利用。
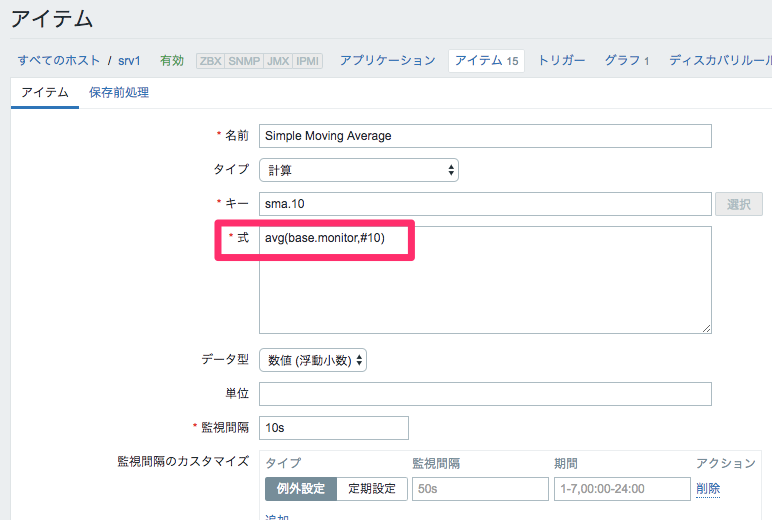
設定方法
10秒間隔で直近10個の監視データの平均を算出して監視結果として登録。
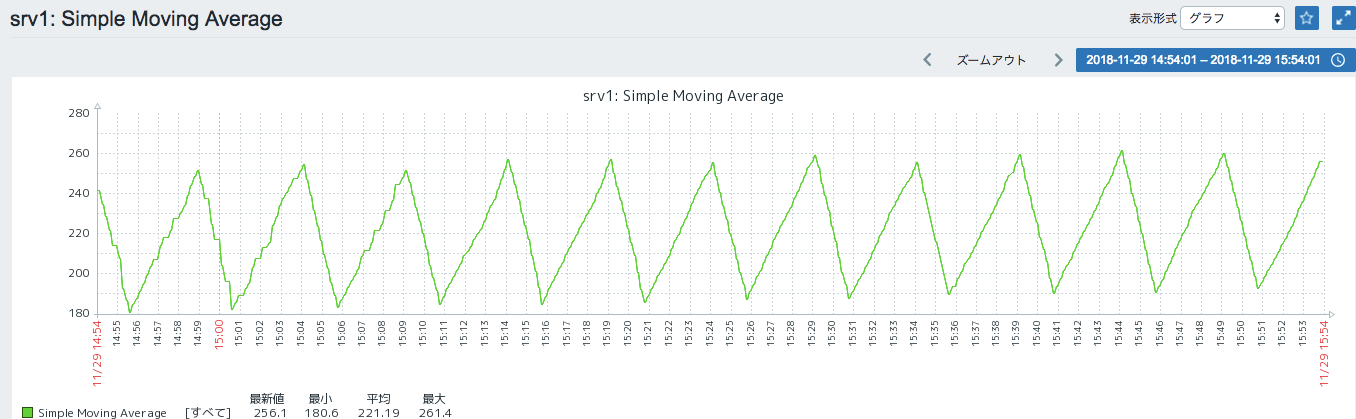
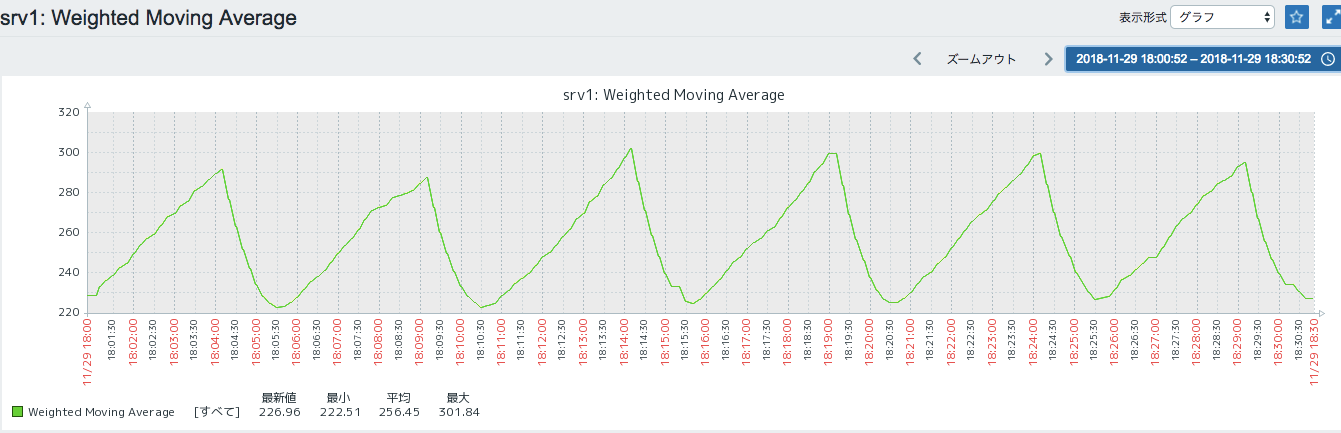
こんな感じで生データよりは平滑化されたグラフが得られます。
平均を算出する対象のデータの個数を増やせばもっと均されます。
加重移動平均
計算式
tの時点における直近n個の監視データ(x)に対し、直近の値に対する重みをnに設定して1ずつ重みを減らす場合の加重移動平均値yの式
y_t = \frac{n \times x_t+(n-1) \times x_{t-1}+ (n-2) \times x_{t-2}+\cdots+x_{t-n+1}}{n + (n-1) + (n-2) + \cdots + 2 + 1}
算出の方針
単純移動平均と同じくトリガー関数のavgを利用し、直近x件の監視データの平均値を算出する計算アイテムを利用。
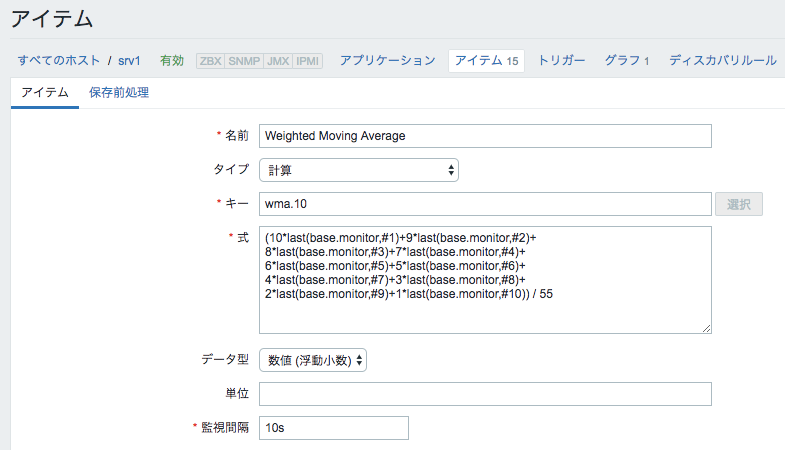
設定方法
10個の監視データを一つずつ重みを変えて掛け合わせる式を記述します。
あまりシンプルにはかけないです。。
先程と同じく平滑化されてますね。
指数平滑移動平均
計算式
係数をαとした場合のtの時点における指数平滑平均値yの式
y_t = α \times x_{t-1} + (1 - α) \times y_{t-1}
算出の方針
- 最初、単純移動平均を求める計算アイテムとして登録(指数平滑平均の値を求めるには最初の1点の値は別の方法で算出した値をなにか設定しないといけないため)
- 途中から計算方法を変えて、前回の監視結果と前回の平均値から計算するアイテムを設定
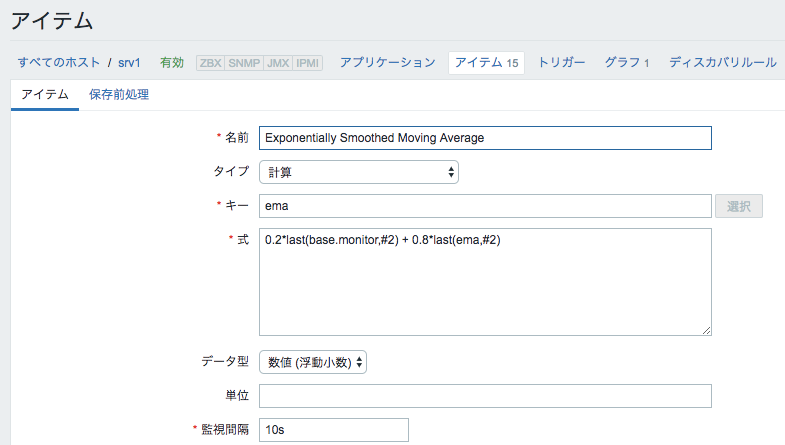
設定方法
係数を0.2(20%)と設定した場合の設定例です。
初回のデータが何か登録されている必要があるので、最初は単純移動平均のときと同じようにavgで算出した設定値を登録し、その後以下の内容に変更しています。
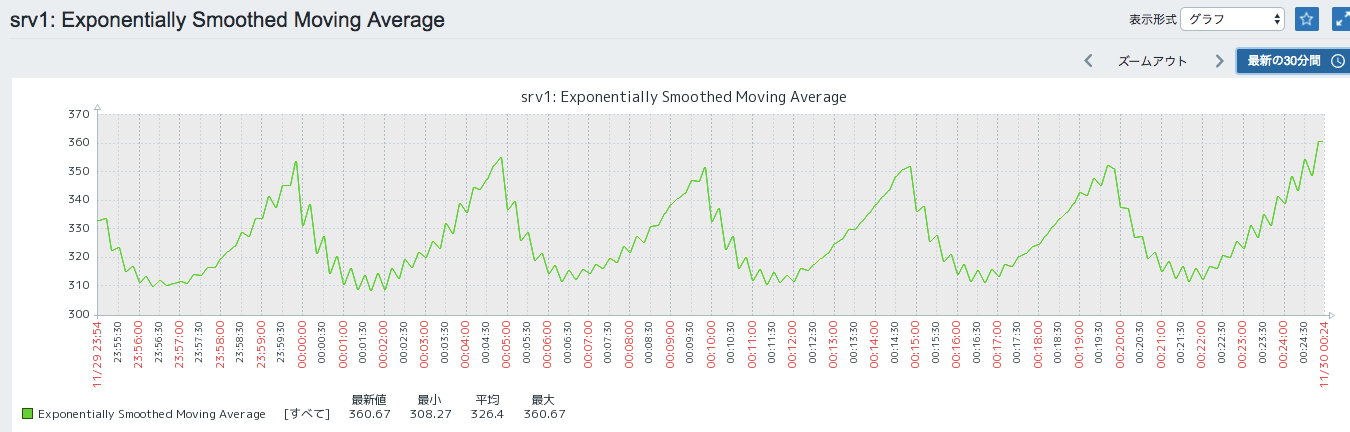
少しいびつな感じですね。。
中央値
計算式
過去の監視結果個数n(偶数個)の中央値yの式
y_t = \frac{x_{t-\frac{n}{2}-1} + x_{t-\frac{n}{2}}}{2}
過去の監視結果個数n(奇数個)の中央値
y_t = x_{t-\frac{n+1}{2}-1}
算出の方針
- percentile関数を使って50パーセンタイル値を算出する計算アイテムを利用
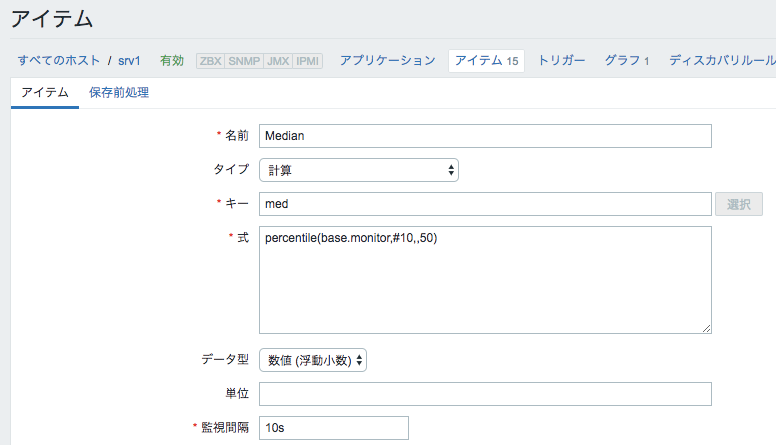
設定方法
percentile関数の第2引数で50%指定にすればOKです。
自己相関係数
計算式
監視結果n個に対し、ラグ(遅れ)がk個の自己相関係数yの式
y_t = \frac{(x_{k+1}-\bar{x})(x_1-\bar{x})+(x_{k+2}-\bar{x})(x_2-\bar{x})+\cdots+(x_{n}-\bar{x})(x_{n-k}-\bar{x})}{(x_{1}-\bar{x})^2+(x_{2}-\bar{x})^2+\cdots+(x_{n}-\bar{x})^2}
算出の方針
- ① n個毎の監視結果の平均値を計算するアイテムを登録
- ② 各監視結果と①の差分を計算するアイテムを登録
- ③ ②の値の2乗を計算するアイテムを登録
- ④ 計算式の分子の加算のために必要となるラグ分ずらした差分と差分を乗算するアイテムを登録
- ⑤ ③の和と④の和を使って自己相関係数を計算する計算アイテムを登録
設定方法
今回の元データが300秒毎に周期的な変動が起こってそうな疑似データだったので、ラグを30個(300秒)の自己相関を求めてみます。
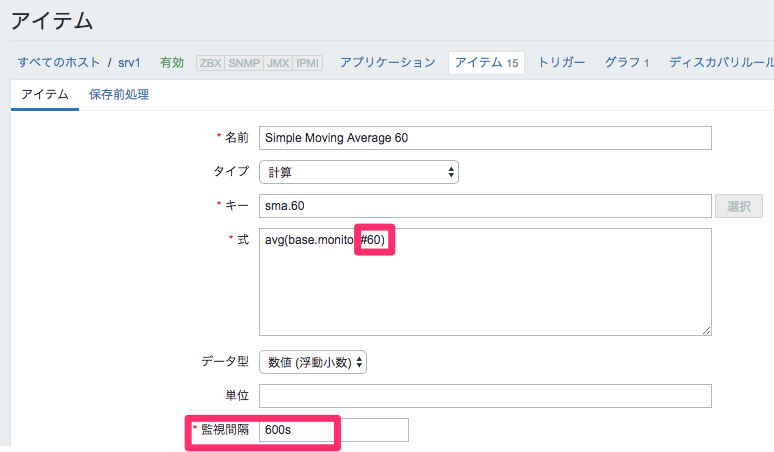
① ひとまず60個毎の監視結果の平均値を計算するアイテムを登録
60個(600秒)分の平均値を600秒に1回算出
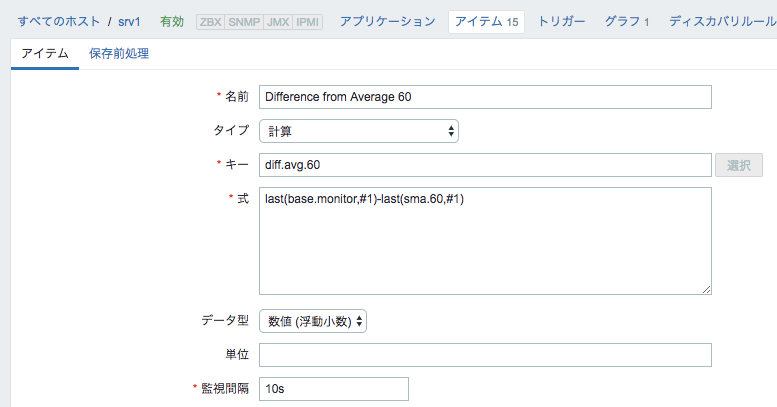
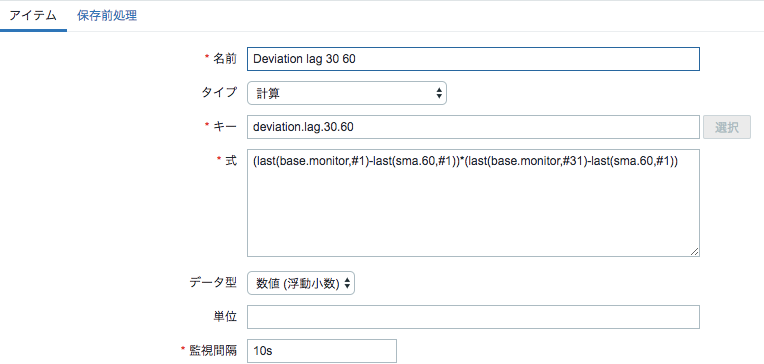
② 各監視結果と①の差分を計算するアイテムを登録
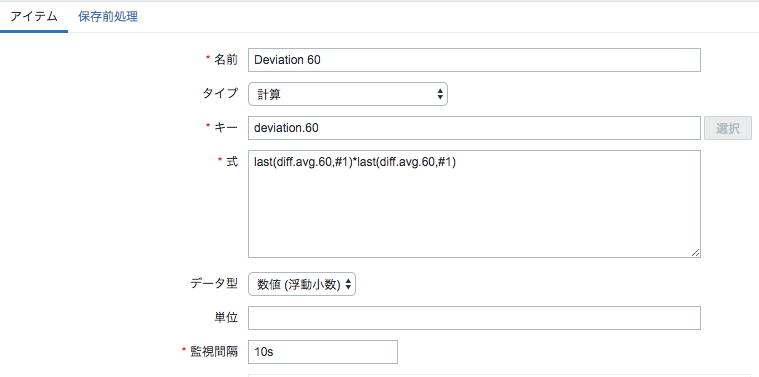
③ ②の値の2乗を計算するアイテムを登録
④ 計算式の分子の加算のために必要となるラグ分ずらした差分と差分を乗算するアイテムを登録
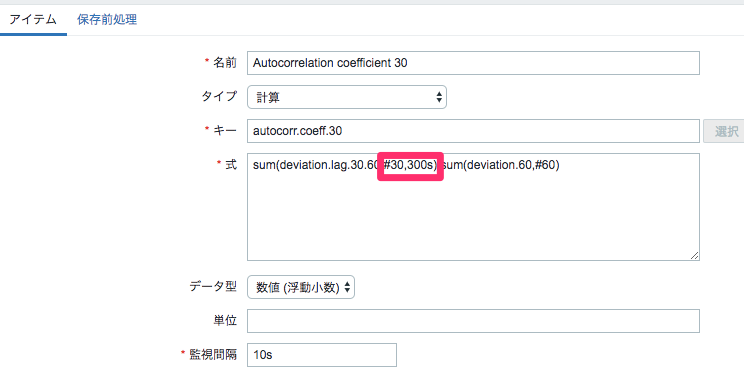
⑤ ③の和と④の和を使って自己相関係数を計算する計算アイテムを登録
sum関数の第2引数でタイムシフト(300秒分前)設定でずらした値を計算させるのがポイント。
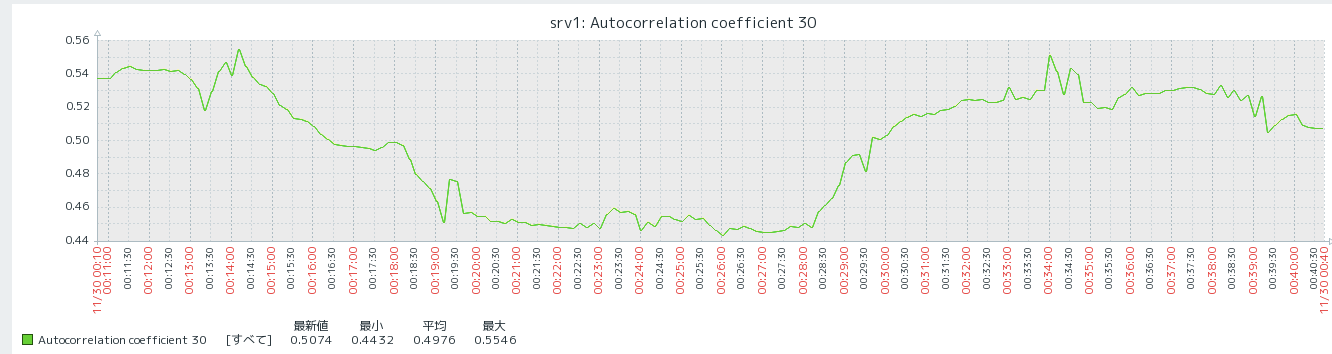
こんな感じで、0.5付近で前後するような自己相関係数の推移が見れます。
ラグ300秒の自己相関を見る限り、正方向の相関がありそうだとわかります。(300秒の周期性がありそうな感じ)
まとめ
他にも時系列のデータ分析としては、AR、MA、ARMA、ARIMA等様々なモデルで分析できますが、さすがにZabbixの計算機能だけではちょっと限界がありそうです。
\sqrt{x}
とか
\log{x}
とかの計算への対応は難しかったりするのであまり複雑なことはできないですが、生のデータ1つでもいろいろと視点を変えてみると見えることも出てきそうですね。冒頭でも記述してますが、分析自体はやはり専門のツールとか、自前でプログラムを組むとか実際には切り出して考えた方がいいかと思います。