まえがき
大学院受験の勉強してたら電磁気の教科書に「等角写像」なる概念が書いていた。
どうやら電位のラプラス方程式を解くために導入されたものであるが、僕は式で理解するのは甘い卵焼きと同じくらい苦手なのでパイソン様に教えてもらうことにした。
数学、物理、Python全てにおいてへっぽこ丸なので恐竜の赤ちゃんを見るドラちゃんくらい温かい目で見てください。
目次
1.複素関数とは
2.等角写像とは
3.等角写像をPythonで
4.まとめ
1.複素関数とは
まずこの知識が怪しかったのでwiki君に聞いてみた。
複素解析(wikipediaのページ)
巷では話好きで有名である彼であるが、要領を得ないとも聞く。
実際よく分からない。
習ったはずなんだけどなぁ
僕の拙い知識を述べると、複素関数とは二次元平面上の点を複素数を使って表す分野。と思う。
「二次元平面上の点を指定するだけならベクトルでも構わないが、複素関数ではひとつの複素数を与えるだけで平面上の一点を特定できるという利点がある。その代わりベクトルのように三次元への拡張は出来ない。」みたいなことが昔読んだ本に書いてあったような気がする。
「複素関数とは」という目次だが、下手に僕の知識を話しても誤解を生みそうなのでここまでにする。
2.等角写像とは
複素関数の説明がテキトーだったのでどうせ等角写像もだろ?と思った方。なかなか鋭いですね。
複素関数自体理解していないのに等角写像なんて理解できるのだろうか?
てか等角って何スカ、写像って何スカ。
そもそも写像という言葉自体一般的ではない。ひろゆきも言ってたし。
御託はこの辺にして本題に戻ろう。
僕は写像というものはある値が与えられたとき、何かしらの処理を行って返す機械のようなものだと思っている。
ソーダサーバーに焼酎を与えるとチューハイが返される、ウイスキーを与えるとハイボールが返される。何も与えなかったらソーダが返される。
写像とはこのソーダサーバーのようなものだ。
少しコードを交えて数学をすると
x=np.array([1,2,3])
y=np.array([1,1,1])
plt.scatter(x,y)
plt.show()
この何の面白みのない点をソーダサーバーにかけてやると
def soda_server(x):
return x**2
x=np.array([1,2,3])
plt.scatter(x,f(x))
plt.show()
一つの点に対してある法則に基づいた点が返されていることが分かるだろう。
写像とはこういうことなのである。
等角とは?
・・・・・
以下のサイトにより詳しく書いている。
僕より1e10倍詳しく説明しているので是非参考にしてほしい。
3.等角写像をPythonで
よりやろう。
適当に複素数をとってそれをソーダサーバーにかけてやるとするか。
まずはソーダサーバーをいくつか用意しよう
それでは
いかれたメンバーを紹介するぜ!!!
三角関数の世界からこんばんWhatup!!!!
sin!!!
def sin(z):
return np.sin(z)
二乗なら俺に任せろ!!
z2!!!
def z2(z):
return z*z
なんか複素関数の教科書の例題によく出てくるやつ!!
h!!!
def h(z):
return (z - 1j)/(z + 1j)
さぁこいつらをつかってどう料理してやろうかって感じなんですけども~・・・
まずx、yの組を用意します。
import matplotlib.pyplot as plt
import numpy as np
s = 3
x = np.linspace(-s,s,100)
y = np.linspace(-s,s,100)
メッシュを切ります
X,Y=np.meshgrid(x,y)
X=X.flatten()
Y=Y.flatten()
点がいっぱいありますね。以上
ソーダサーバーに通すとこの点たちはどう変わるのでしょうか?
Z=np.zeros([Y.shape[0]],dtype=complex)
for i in range(Y.shape[0]):
x=X[i]
y=Y[i]
z=sin(x+1j*y)
Z[i]=z
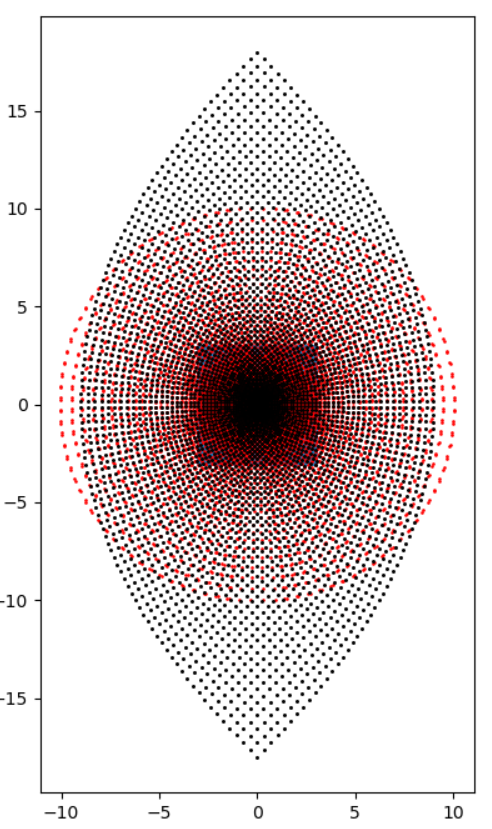
plt.scatter(Z.real,Z.imag,color="red",s=0.8)
なんか広がりましたね。
次
Z=np.zeros([Y.shape[0]],dtype=complex)
for i in range(Y.shape[0]):
x=X[i]
y=Y[i]
z=z2(x+1j*y)
Z[i]=z
plt.scatter(Z.real,Z.imag,color="black",s=0.8)
plt.show()
レモンみたいにしようと思って黄色だったんですが、見にくいので黒にしました。
4.まとめ
写像したら点が動きましたね。
等角の説明するには線で説明する必要があったのですが、リンクのコードがいまいち理解できなかったので点で書き直してみたら本質を見失ってしまいました。
等角写像による画像の変換〜Schwarz-Christoffel 変換〜 part1
最後に、ここまで読んでいただきありがとうございます。
Youtubeだったら低評価の方が多いような記事ですがこれからもちょくちょく更新していこうと思います。
よかったらまた見てください。