数値計算で使用される様々な境界条件についてまとめてみる。
問題設定
１次元波動方程式を差分法にて数値計算する問題を考える。今回考える方程式を以下のように与える。
\frac{\partial^2 u(x,t)}{\partial t^2}=\frac{\partial^2 u(x,t)}{\partial x^2}
ここで、$0\leq x \leq L$、$0\leq t$をとる。初期値として以下を与える。
\frac{\partial u(x,t=0)}{\partial t}=0
また、初期値$u(x,t=0)$は考える境界条件によって変化させる。
差分法
空間方向の$[0,L]$区間を$N$等分するとき、１区画の距離$\delta x$は$\frac{L}{N}$となり、各区画の座標$x_i=i\delta x$となる。また、時間方向への離散化は、$t_j = j\delta t$とできる。このとき、
U_i^j\equiv u(x_i,t_j)
とおく。離散化された１次元波動方程式は
\frac{U_i^{j+1}-2U_i^j+U_i^{j-1}}{\delta t^2}=\frac{U_{i+1}^j-2U_i^j+U_{i-1}^j}{\delta x^2}
となる。左辺に$U_i^{j+1}$だけ残るようにすると、
U_i^{j+1}=2U_i^j-U_i^{j-1}+\frac{\delta t^2}{\delta x^2}(U_{i+1}^j-2U_i^j+U_{i-1}^j)
となり、時間発展を漸化式で表すことができる。
境界条件
この問題設定のもと、様々な境界条件$u(x=0,t)$、$u(x=L,t)$を考えていく。
ディリクレ境界条件
第１境界条件とも呼ばれ、境界上の点$x$に対して、
u(x)=f(x)
という条件を与える。
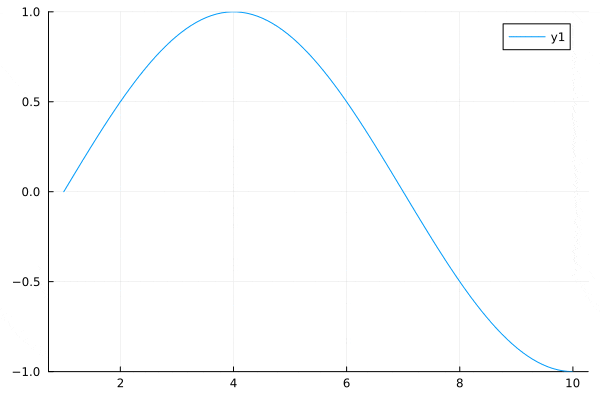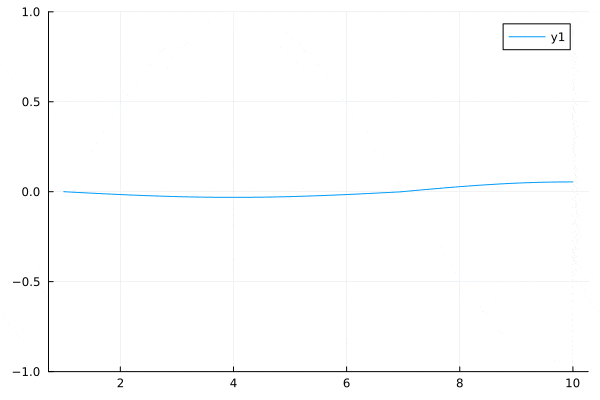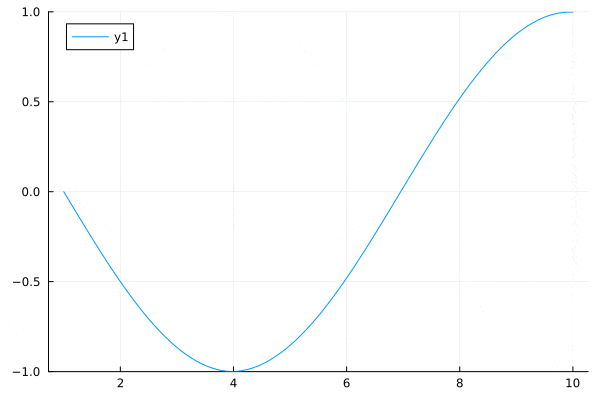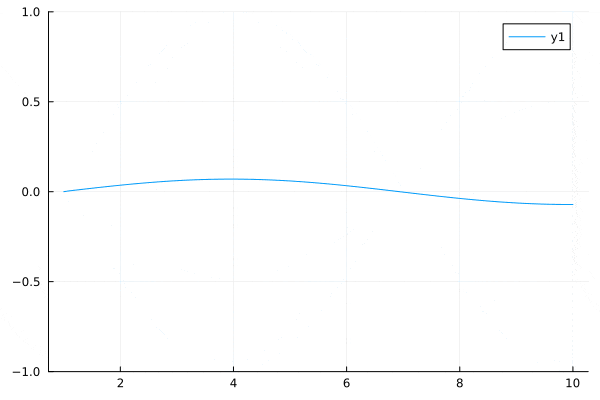
数値計算
初期値$u(x,t=0)=\sin(2\pi x)$とする。
ディリクレ境界条件は、
\begin{multline}
\begin{split}
u(x=0,t)&=0\\
u(x=L,t)&=0
\end{split}
\end{multline}
で与える。
このとき、数値計算結果は下図の通り。
両端が常に$0$となっており、固定端と呼ばれる。
ノイマン境界条件
第２境界条件とも呼ばれ、境界上の点$x$に対して、
\frac{\partial u(x)}{\partial x}=f(x)
という条件を与える。
数値計算
初期値$u(x,t=0)=\cos(2\pi x)$とする。
ノイマン境界条件は、
\begin{multline}
\begin{split}
\frac{\partial u(x=0,t)}{\partial x}&=0\\
\frac{\partial u(x=L,t)}{\partial x}&=0
\end{split}
\end{multline}
で与える。
このとき、数値計算結果は下図の通り。
自由端と呼ばれる。
ロビン境界条件
第３境界条件とも呼ばれ、境界上の点$x$に対して、
au(x)+b\frac{\partial u(x)}{\partial x} = f(x)
という、ディリクレ境界条件とノイマン境界条件の線形結合を与える。
数値計算
良い感じの初期値を探し中。
ノイマン境界条件は、
\begin{multline}
\begin{split}
u(x=0,t)+\frac{\partial u(x=0,t)}{\partial x}&=0\\
u(x=L,t)+\frac{\partial u(x=L,t)}{\partial x}&=0
\end{split}
\end{multline}
で与える。
混合境界条件
境界を複数の部分集合に分割し、それぞれの部分集合で異なる境界条件を組み合わせること。
数値計算
初期値は$u(x,t=0)=\sin(\frac{3}{2}\pi x)$とする。
混合境界条件は、
\begin{multline}
\begin{split}
u(x=0,t)&=0\\
\frac{\partial u(x=L,t)}{\partial x}&=0
\end{split}
\end{multline}
で与える。
このとき、数値計算結果は下図の通り。
コーシー境界条件
境界上の点$x$に対して、
\begin{multline}
\begin{split}
u(x)&=f(x)\\
\frac{\partial u(x)}{\partial x}&=g(x)
\end{split}
\end{multline}
という、ディリクレ境界条件とノイマン境界条件の両方を与える。
数値計算
良い感じの初期値を探し中。
コーシー境界条件は、
\begin{multline}
\begin{split}
u(x=0,t)&=0\\
\frac{\partial u(x=0,t)}{\partial x}&=0
\end{split}
\end{multline}
で与える
周期境界条件
境界上の点$x$に対して、
u(x)=u(x+L)
という条件を与える。
数値計算
初期値は$u(x,t=0)=\sin(2\pi x)$とする。
周期境界条件は、
u(x)=u(x+L)
で与える。
このとき、数値計算結果は下図の通り。
ボルン=フォン・カルマン境界条件
波動関数がある特定のブラベー格子上で周期的でなければならないという周期境界条件。固体物理学いｎおいて理想結晶をモデル化するために用いられる。
ヘリカル境界条件
？