株価の相関関係を可視化したい
※2022年6月時点の分析のため、分析期間や銘柄名などに違和感があるかと思われますがご容赦ください。
1. 目的
今回やりたいこと
今回の分析では、株式1銘柄を点(以下ノード)、各銘柄間の相関を線(以下リンク)と見立て、特定の市場全体の株価の相関関係をグラフ化したい。このとき銘柄間のつながりをどう定義するか、がモデルの肝となる。今回は、「直接相関と間接相関」という2つ関係性の違いに着目しモデルを定義していきたい。
直接相関と間接相関を区別する
直接相関と間接相関を定性的に理解するには、以下の例がわかりやすい。
ある日の気温が高いとき、当然かき氷屋の売上が上がる。単純に考えると、気温が高くなるほど売り上げが増加する。この2つの関係性を「直接相関」という。同じように、気温が高いほどエアコンの使用が増え、家庭の光熱費が増加するため、気温と家庭の光熱費にも「直接相関」があると言える。(冬は暖房で光熱費が上がるというのは一旦無視したとして)このとき、かき氷屋の売上と家庭の光熱費にも相関関係が生まれてしまう。直感的に考えたとき、家庭で光熱費が高まってもかき氷屋の売上に影響はないが、2つのデータを並べたときにそこには相関関係が生まれてしまう。それが、「間接相関」である。簡単に言えば、相関関係の内、因果関係があるものが直接相関、ないものが間接相関、と考えて問題ない。
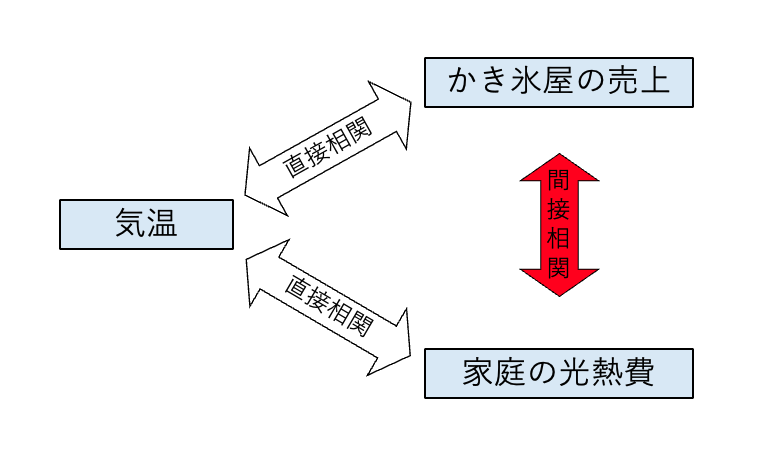
今回の研究では、リンクを定義する際に「間接相関」、つまり見せかけの値動きの相関を排除して、直接的な株価相関だけを反映したい。
このとき、「直接相関」、つまり「この銘柄が上がれば、この銘柄が上がりやすい」という銘柄間の結びつきを全て定性的に判断するのは現実的ではない。ここで、「グラフィカルラッソ」という定量モデルをリンクの定義に使用する。
2. グラフィカルラッソ
※もちろん、2つのデータの相関が直接相関か間接相関かの真偽は定性的に判断しない限り本当のところはわからない。このモデルはあくまで、いくつかの仮定の基、「定量的に直接相関を示すと考えられるデータ」を計測しているだけにすぎない、ということには留意すべきである。
偏相関係数とは・・・
詳しい計算過程の説明は参考書に譲るが、グラフィカルラッソでは多変量正規分布を想定したマルコフグラフを構成することを考える。
このとき、各成分に標準化変換を施したM次元データ$D=[x^{(1)},x^{(2)},...,x^{(M)}]$の確率分布関数は以下で表される。
$$
\mathcal{N}(x|0,\Lambda^{-1})\equiv \frac{|\Lambda|^{1/2}}{(2\pi)^{M/2}}\exp(-\frac{1}{2}x^{T}\Lambda x)
$$
ただし、$\Lambda$は共分散行列の逆行列であり、精度行列ともいう。このときパラメータは精度行列一つで表せれていることが重要となる。
ここでたとえば、$x^{(1)}$と$x^{(2)}$の関係性を考える。直接相関を考える場合、「他の変数がどのような値でも互いの依存関係が見られる」ことを確認する必要があるため、条件付き確率 $p(x^{(1)},x^{(2)}|x^{(3)},...,x^{(M)})$を調べる。
確率分布関数を基にすると以下のように計算できる。
$$
p(x^{(1)},x^{(2)}|x^{(3)},...,x^{(M)})\propto \exp[-\frac{1}{2}(\Lambda_{1,1}x^{(1)}x^{(1)}+2\Lambda_{1,2}x^{(1)}x^{(2)}+\Lambda_{2,2}x^{(2)}x^{(2)})]
$$
上の式より、すぐに$x^{(1)}$と$x^{(2)}$が統計的に独立であるためには$\Lambda_{1,2}=0$である必要があり、逆が言えることも明らかである。
よって、
$$
r^{i,j}\equiv\frac{\Lambda_{i,j}}{\sqrt{\Lambda_{i,i}\Lambda_{j,j}}}
$$
を偏相関係数と言い、この値が0でなければ「$x^{(i)}$と$x^{(j)}$には直接相関がある」と表現できる。
ちなみに$\Lambda_{i,j}=0$かつ$\Sigma_{i,j}\neq0$であるとき、「$x^{(i)}$と$x^{(j)}$には間接相関がある」と表現できる。
したがって、$\Lambda$の導出が直接相関、すなわち今回定義したいリンクの接続基準に直結するということになる。
グラフィカルラッソモデル
今回目的としているグラフの構築を含む構造学習の目的は、「直接相関の構造を浮かび上がらせること」にある。そういう意味で、グラフはノイズとなる相関を排除し疎なグラフがふさわしい。つまり、$\Lambda$の成分は大半が0であることが好ましい。
このとき、単純に最尤推定などで$\Lambda$を推定した場合、大きく2つの問題が生じる。
①分散共分散行列が正則であることが求められる。
②たとえ正則であったとしても、$\Lambda$の成分の多くが0でなくなる。このとき、どこかの閾値で0に切り捨てても、その閾値に結果が敏感に左右される。
したがって、構造学習の中に明示的に精度行列の疎性を取り込む必要があり、それを実現したのが「グラフィカルラッソモデル」である。
グラフィカルラッソモデルの隣接行列$\Lambda^{*}$は以下に従って求める.
${}$
<パラメータ推定>
$$
\Lambda^{*}=argmax f(\Lambda;S,\rho)
$$
$$
f(\Lambda;S,\rho)\equiv ln\ det\Lambda -tr(S\Lambda)-\rho\lVert \Lambda \rVert_1
$$
ただし、$S$は標本共分散行列、$\lVert \Lambda \rVert_1$は$\sum_{i,j=1}^M|\Lambda_{i,j}|$とする。
細かい数式の説明は省くが、重要なことは正則化パラメータ$\rho$によって、$\Lambda$を0付近に束縛している部分であり、これにより、疎な隣接行列を構成している。
※上の数式を繰り返し計算するプログラムを構成するだけでもかなり骨が折れると想像されるが、pythonには便利なことに「GraphicalLassoCV」というモジュールが搭載されており、実際の分析では、分析データと正則化パラメータを設定するだけで精度行列$\Lambda$が出力される。
株価分析に適用すると・・・
では、今回のお題目である株価リターンを分析データとした場合、グラフィカルラッソがどれだけの威力を発揮するか。
まず一般的な相関行列で株価のリターンを相関をヒートマップ化すると以下のようになる。
一般的な相関行列の例
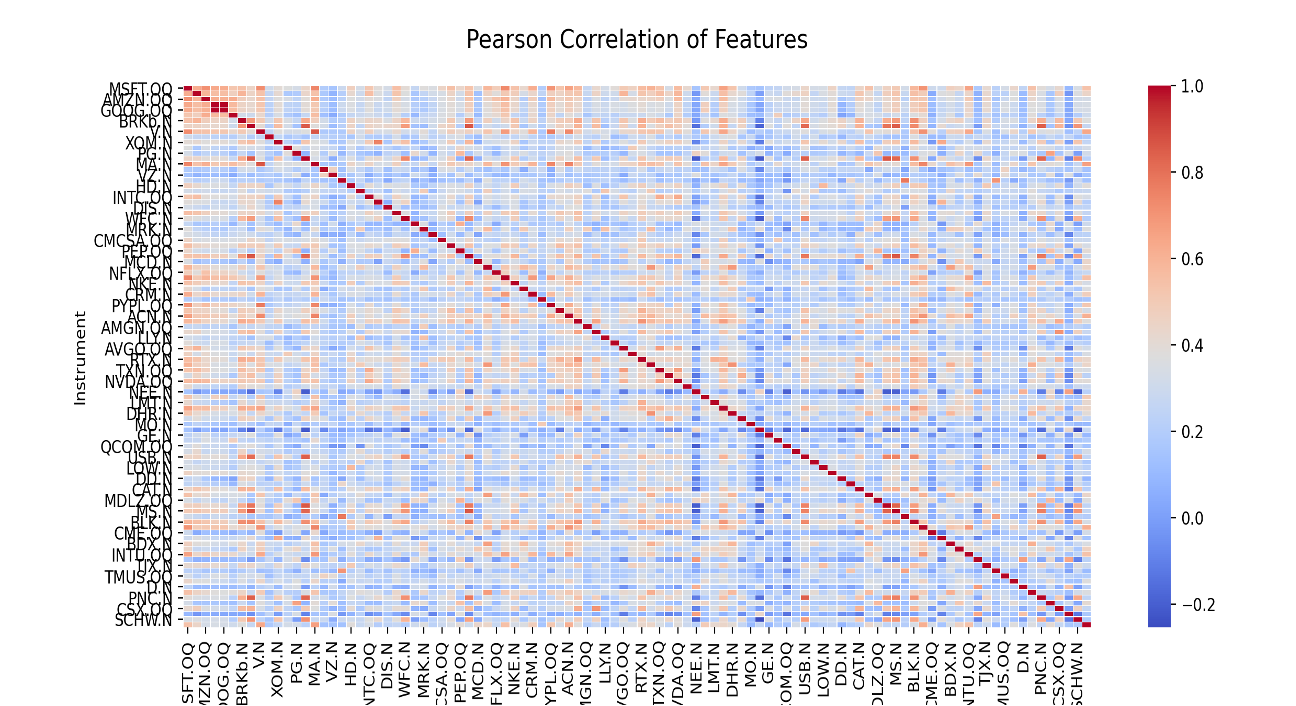
今回は分かりやすく分析対象は米株の時価総額上位100銘柄(2019年末時点)を対象としてる。相関が高いほどセルが赤く点灯するが、至る所に高い相関が計測されていることが分かる。
一方、グラフィカルラッソにより計測された精度行列$\Lambda$の
ヒートマップはどうなっているか。
グラフィカルラッソの使用例
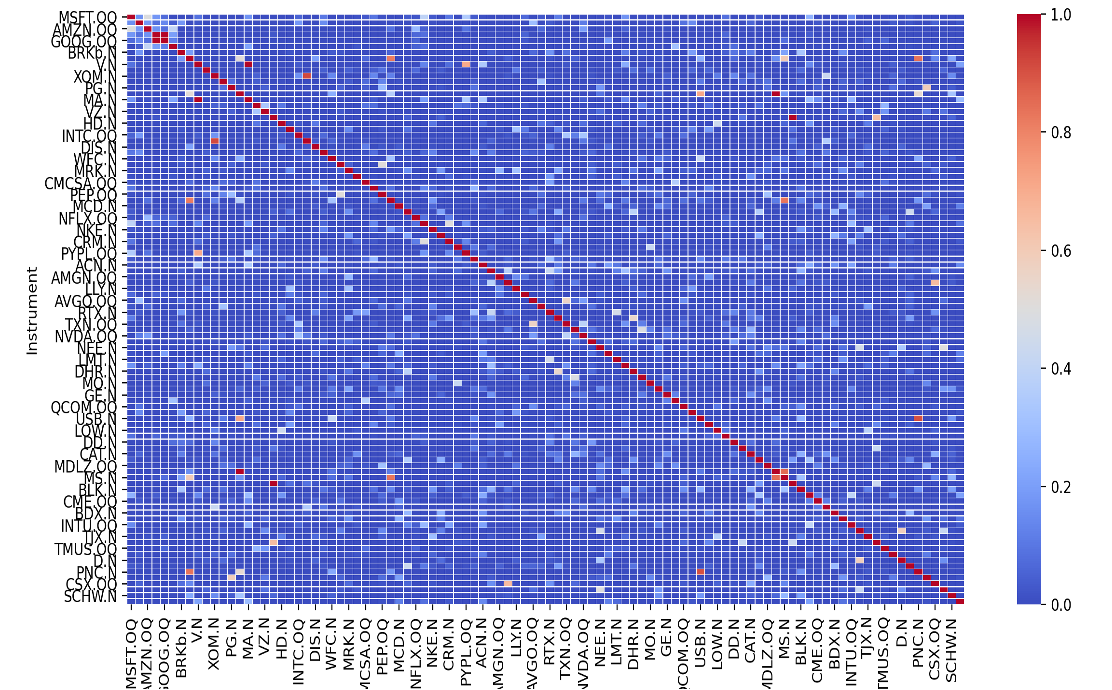
図より、ほとんどの図が青塗り、つまり無相関となっており、わずか赤く点在していることがわかる。ちなみに偏相関係数は正負の方向が一般的な相関の正負と対応しているわけではないため、偏相関係数は絶対値の大きさで計測している。つまり、この赤く点在している点がグラフィカルラッソで導き出された「直接相関」であり、これらをリンクさせたグラフを構築するイメージである。
このようにグラフィカルラッソは疎なグラフを構築することに適している。上の相関行列で閾値を設定して、下のグラフに寄せれば良いと考えるかもしれないが、その場合結果がパラメータに敏感に左右されてしまい、結果の安定性が損なわれてしまう。
3. ネットワーク構築
それでは今回の趣旨であるネットワークの構築に移っていく。
分析条件は以下の通りである。
${}$
<分析概要>
- 分析期間:2006年初〜2019年末
- 分析対象銘柄:S&P500時価総額上位100銘柄(2019年末時点)
- 正規化パラメータ:$\rho=0.1$
- 銘柄$i$と銘柄 $j$をリンクさせる(関係性を持つ)
$\Leftrightarrow|\Lambda_{i,j}|>0.1$
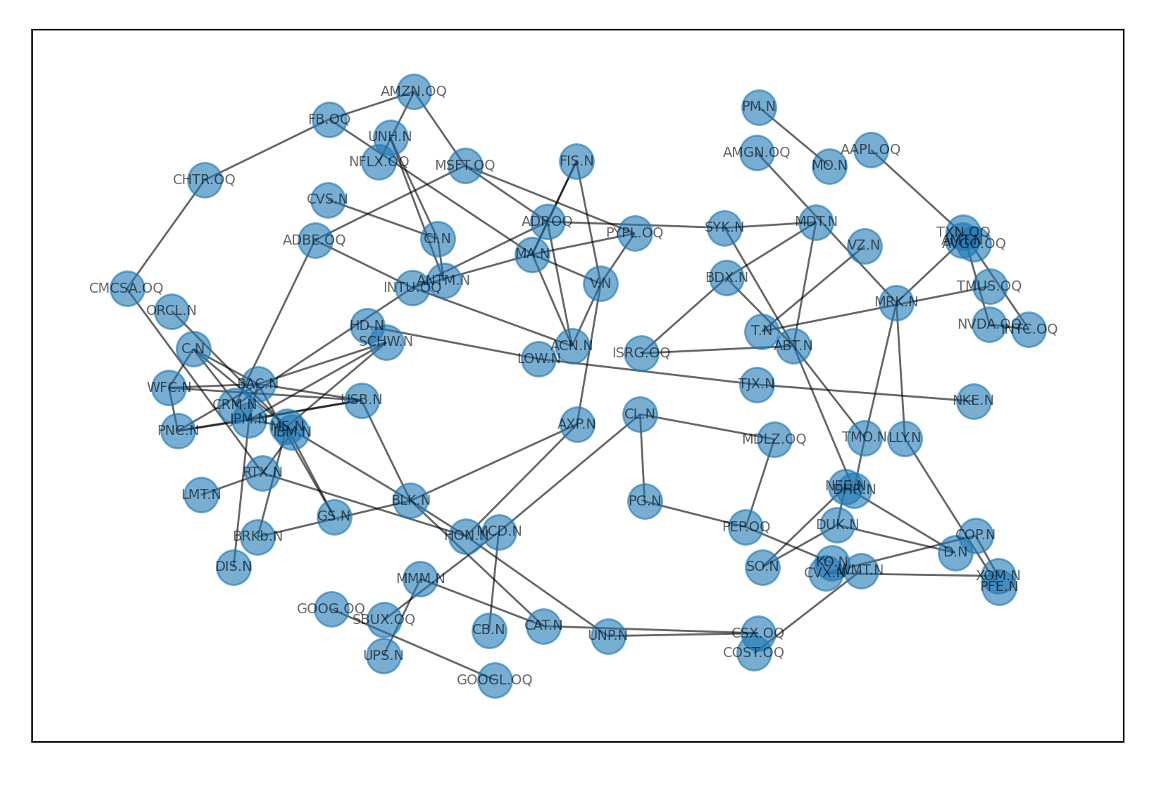
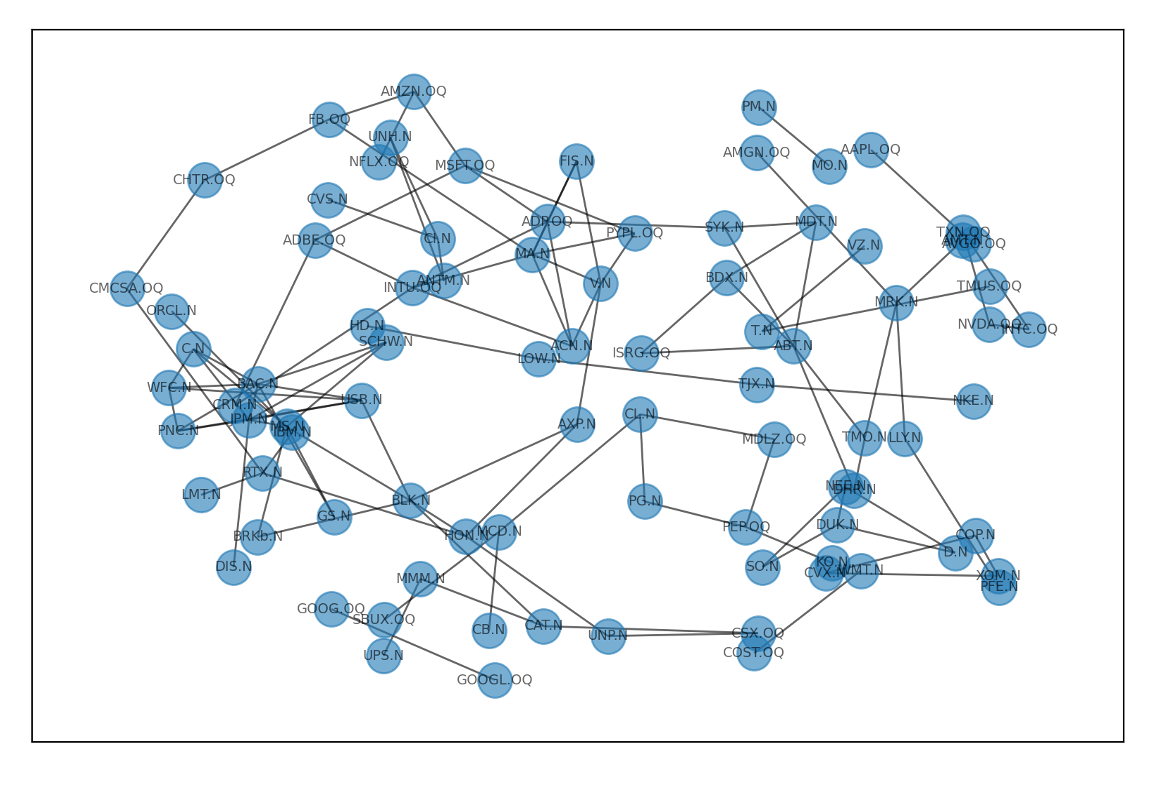
上記条件の元、構築したネットワークが以下である。
ネットワーク構築例①
※ネットワークの構築にはpythonモジュールの「pyvis.network」を用いた。
グラフィカルラッソによって銘柄間の繋がりを視覚的に把握可能なグラフが作成できたことが分かる。ただ、せっかくネットワーク化するのであればもう少し視覚情報を増やしたいところである。
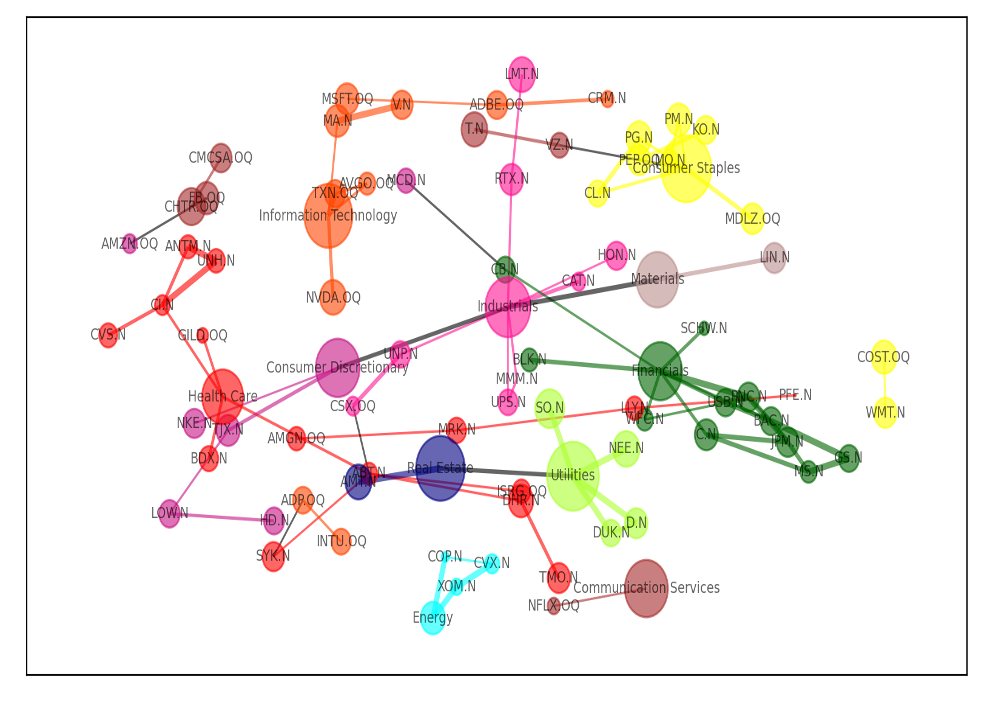
そこで、以下のようにグラフをカスタマイズした。
ネットワーク構築例②
ネットワーク例①からアップデートさせた部分は以下の通りである。
${}$
<アップデート部分>
- 銘柄をセクターごとに色分け(セクターはGICS11セクターを使用)
- セクター(同セクター銘柄の平均)を表すノード(頂点)を追加
⇨セクター間の関係性も可視化するため - 計算に使用するリターンをトータルリターンから市場の影響を除いたレジデュアルリターンに変更
⇨β(市場の影響)によって誤相関を補足しないようにするため。 - 同セクター内のエッジの色は同色、別セクター間のエッジの色は黒に色付け
- 偏相関係数の大きさに応じてエッジの太さを変更(太い線ほど関係性が大きい)
以上のカスタマイズによって、よりシンプルかつ多角的な情報がネットワークから読み取れるようになったと思われる。
4. 考察
前項まででさまざまなツールを駆使してネットワークという視覚的な情報を取得できたが、構築自体に大きな意味はない。「ネットワークをどう活用するか」ということが重要である。投資における活用案を最後に述べるが、今回は『セクター』という切り口でネットワークから読み取れる情報を考察していきたい。
4-1. GICS11セクター
今回はセクター分類として、GICS11セクターを使用する。
GICS(Global Industry Classification Standard)はS&PとMSCIが定める業種分類であり、グローバルな証券業務・運用業務で常用されている。GICSは階層構造になっており、11セクターの荒い分類から158業種の細かい分類まで4段階あるが、分類が細かすぎると視覚的に理解しづらくなってしまうため、今回は一番荒い11セクターの分類を使用した。
考察に入る前に今一度各セクターの情報を整理した。バリューorグロース、シクリカルorディフェンシブについては、一概にどちらかに分類することはできないが、「セクター内に含まれる銘柄が一般的にどちらの特性に振れているか」という点で分類した。(色はネットワークに対応する色)
GICS11セクター内訳表
以下の分析は上記の表の内容を基に進めていく。
4-2. 分析開始年と終了年を比較
ここからは分析期間=2006年〜2019年の分析開始年と終了年の市場構造を比較していく。
まず、分析開始年=2006年と終了年=2019年、それぞれで構築したネットワークを比較する。
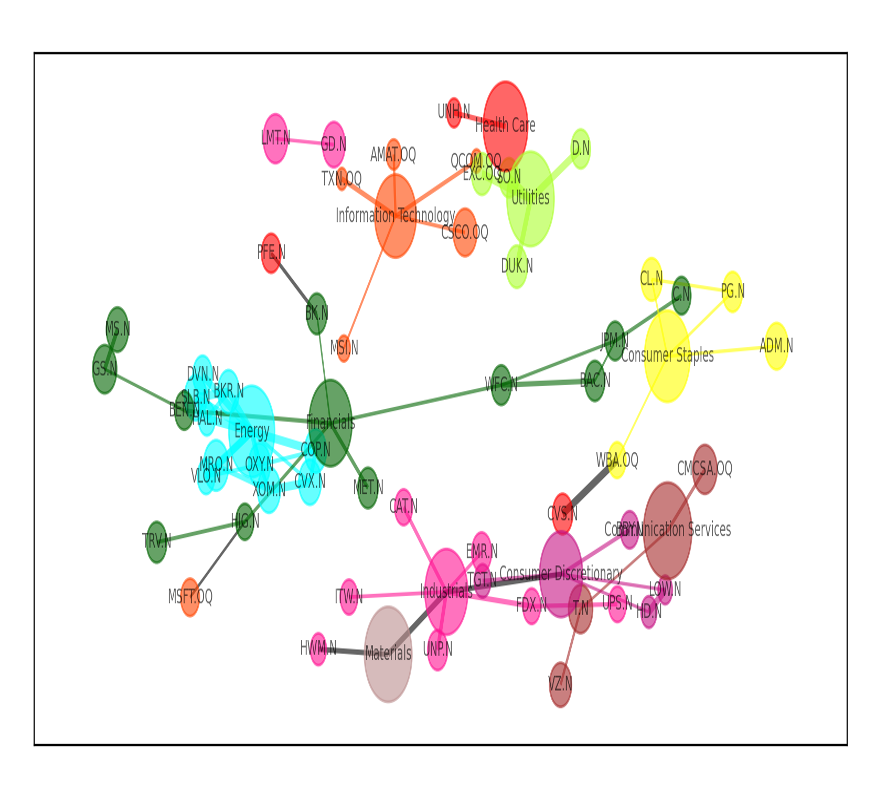
2006年のネットワーク
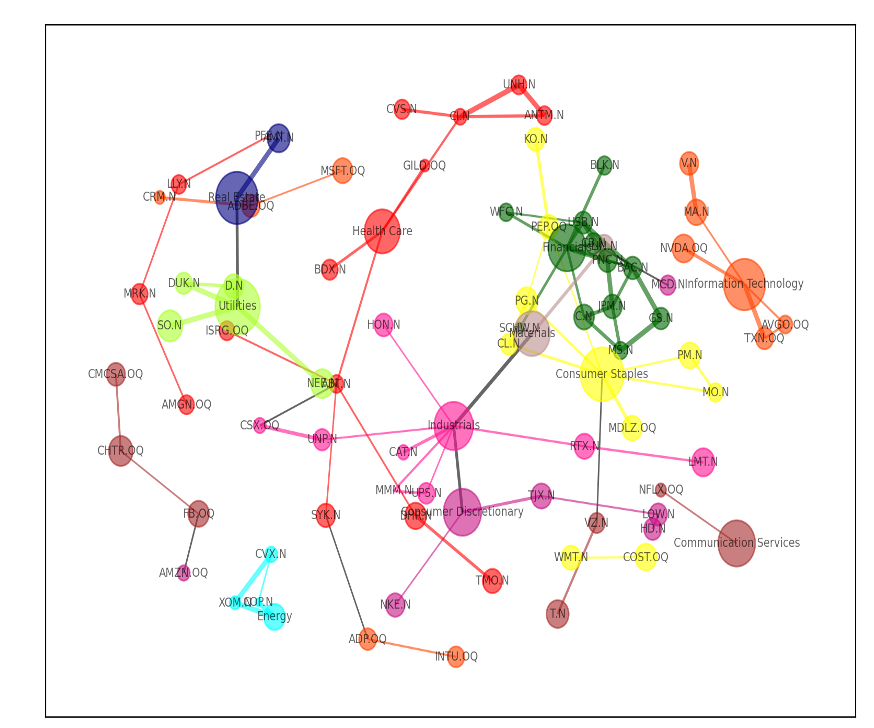
2019年のネットワーク
それぞれのネットワークを比較して分かるのは、各セクター間の距離が最近の市場の方が離れている、つまりセクターごとの株価の連動が薄れてきていることくらいだろうか。(ネットワークの仕様上、関係の強いノード同士は近づく)
次にネットワークの変化をさらに細かく見ていく。
4-3. セクターの平均リンク数と中心性
今回のネットワークから読み取れることは各セクターがどのようなまたはどのくらいセクター・銘柄と、リンクしているかである。そこで、時代の変化によって各セクター間の結びつきが変化しているか、を見ていくこととする。イメージで言えば、時代が経つにつれハイテク銘柄の影響力が高まり、他のセクター・銘柄全体にリンクが伸びていくことが確認できれば興味深いと考えた次第である。
確認する指標は①平均リンク数と②中心性の2つの指標。①はシンプルにセクター内の銘柄、1銘柄あたりの次数(他のノードの結びつくエッジの数)。ただし①だけでは、単に銘柄数の多いクラスターを構築している(他と独立して固まっている)だけのセクターの指標が高くなるため、①と合わせ、②中心性(pagerank)という指標を確認することとした。
②中心性(pagerank)$r_u$の定義は以下の通りである。
$$
r_u=d\sum_{v\in B_u}\frac{r_v}{n_v}+(1-d)\frac{r_u}{N}
$$
ただし、
- $B_u$: 𝑢のリンク先ノードの集合
- $n_v$: $v$の次数
- $N$: ネットワーク全体の総ノード数
- $d$: 𝑢のリンク先ノードの集合
特徴的な部分は右式の第一項にて、リンク先のノードの次数字数まで考慮している点である。つまり、影響力の強いノード(銘柄)との結びつきが高いほど、中心性の指標は高くなる傾向になるため、よりグラフ全体で中心的なポジションとなっているノードを特定することができる。
ただ、上式を解析に解くことはできないため、こちらもpythonモジュールの「nx.pagerank」を使って計測した。(一般的に使われるd=0.85に設定した。)
以下は各時点(3年ごと)の①平均リンク数と②中心性をセクターごとに測定した結果である。データ値は①②のそのままのデータではなく、時点ごとのランキングの数値である。また、各セクターの上位2セクターのデータを赤字、下位2セクターのデータを青字としている。
セクターごとの平均リンク数と中心性
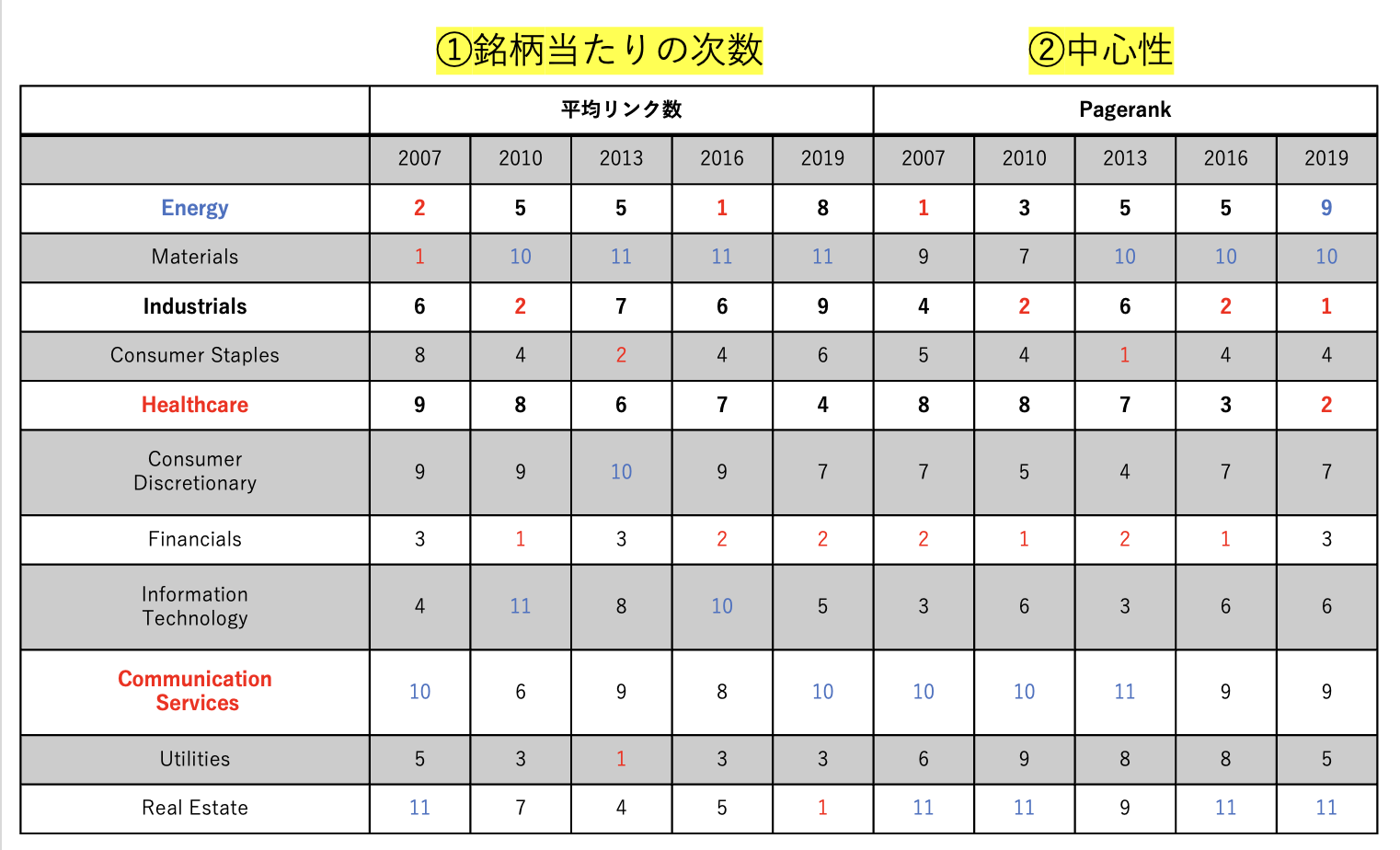
データを一気に並べても考察しずらいだろうが、おおよそ各セクターの位置付けは時系列で大きく変化していないことが分かる。ただし一部セクターでやや変化が見られるため、ここからは特に変化が見られた以下の3セクターに注目していきたい。
(1)Energy(エネルギー)
(2)Healthcare(ヘルスケア)
(3)Communication Services(通信)
4-4. エネルギー・ヘルスケア・通信の影響力の変化
上のランキングでは一見して変化が分かりにくいため、実際の①平均リンク数と②中心性の計測値の時系列推移をそれぞれ確認していきたい。
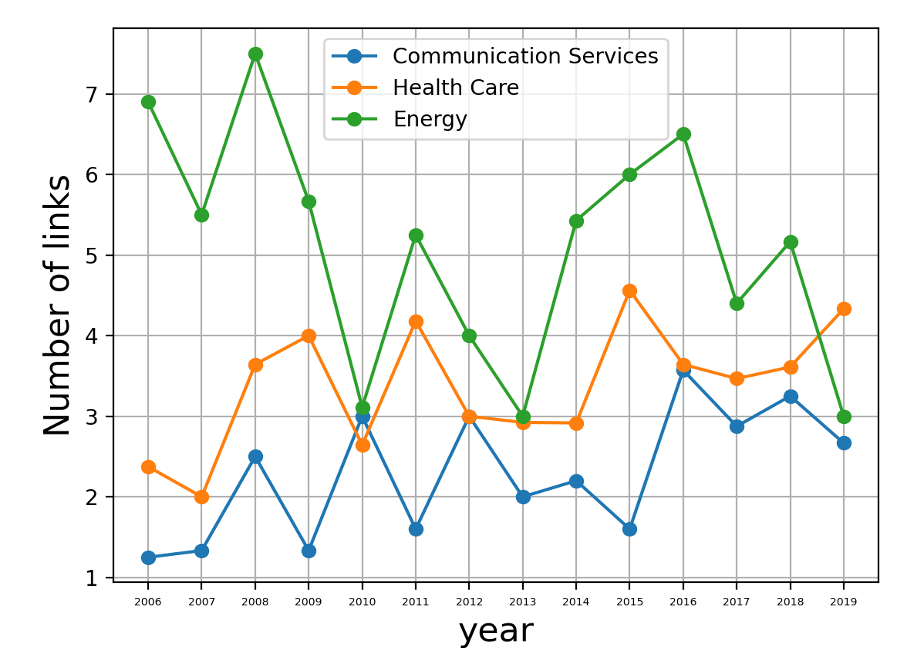
①平均リンク数の推移
②中心性の推移
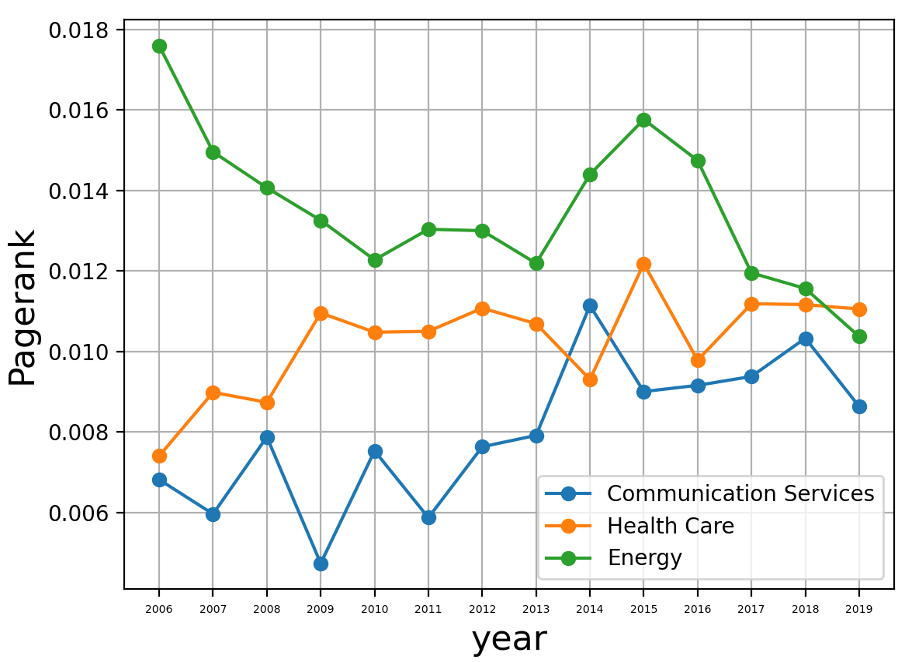
以上のグラフから、多少のブレはあるが、
「ネットワーク(市場)全体で、エネルギーセクターの影響力が低下し、
通信・ヘルスケアの影響力が上昇していること」が分かる。
4-5. リンク先の特性変化
前項まではリンク数という単純な数量の変化を確認した。次にリンク先の特性の変化を確認したい。
ここで上述の「GICS11セクター内訳表」を参照したい。表上では各セクターをバリューorグロース、シクリカルorディフェンシブで分類した。この分類を参考に11セクターをそれぞれ2つの特性で分類した場合、各セクターはどちらの特性と強く結びついているか、を時系列で確認する。
言葉で説明するより、実際に測定した結果を見ると分かりやすい。
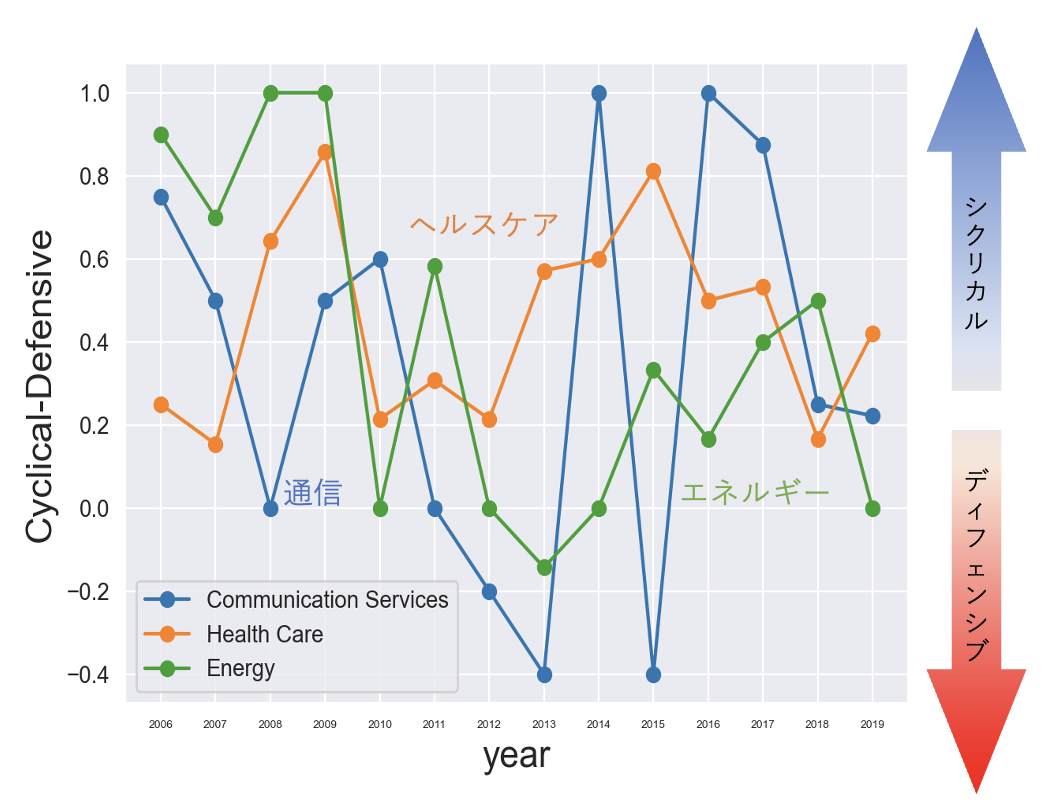
先ほどの3セクターに限定し、測定した。グラフが上に推移すると、シクリカル系のセクターとのリンクが強まっていることを表す。ちなみに、シクリカル系のセクターとは、ビジネスが景気変動の影響を受けやすいセクター(ディフェンシブはその逆)を指す。
エネルギー・ヘルスケア・通信のリンク先の特性変化
ここでは、エネルギーがややシクリカルからディフェンシブに推移したことを除けば、特筆すべき傾向は確認できなかった。
同じような検証を全11セクターに対して行ったところ、以下2セクターの推移が特徴的だったため紹介する。
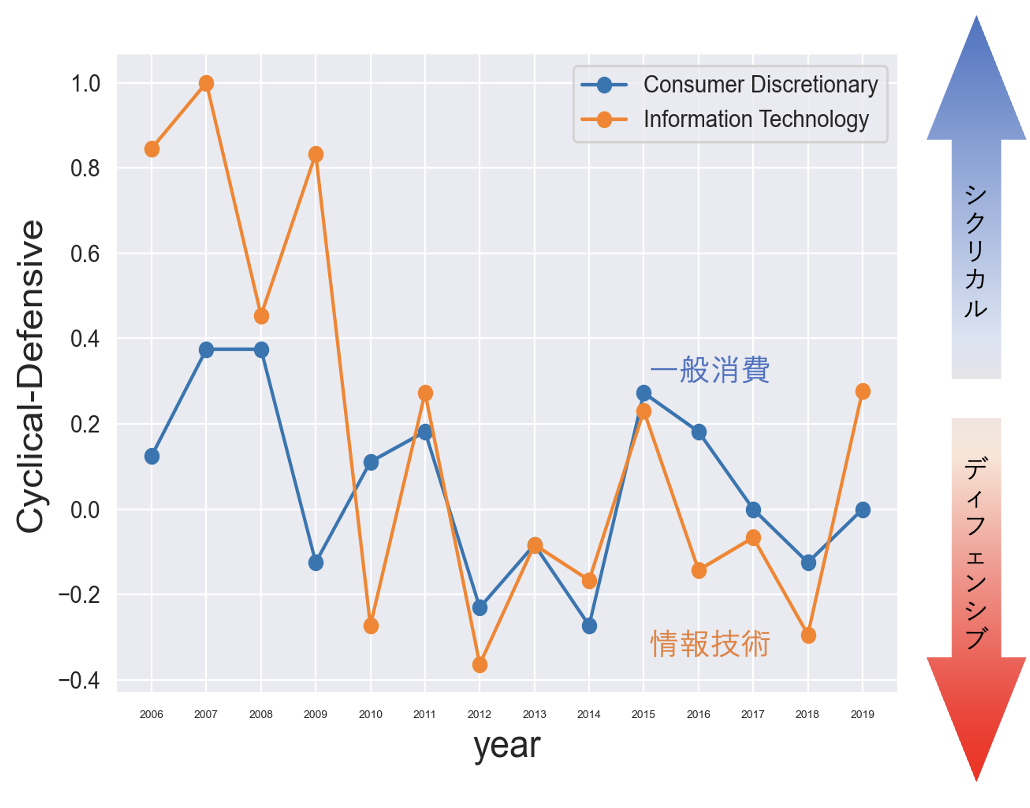
一般消費・情報技術のリンク先の特性変化
グラフから分かる通り、ややブレはあるものの、長期的に一般消費と情報技術はシクリカルからディフェンシブに推移にリンク先の特性が変化している。リンク先の変化は、同セクター自体の特性変化と見ることもできることから、「一般消費セクター・情報技術セクターはディフェンシブ性を高めているのではないか」と考えられる。
${}$
☆ 実際にコロナショック時のセクターごとのパフォーマンスのランキングを確認すると、シクリカルセクターである情報技術・一般消費セクターのダウンサイド耐性は強かった。
1位 情報技術
2位 ヘルスケア
3位 一般消費
4位 通信
4-6. リンク先セクター比率の変化
では、より詳細な情報を確認するためリンク先のセクターがどのように変化していったかを確認する。
以下、シクリカルorディフェンシブの2区分から11セクターに粒度を上げ、リンク数ではなくリンク数の比率の推移を確認する。
数式にすると以下の定義となる。
$$
セクターAのセクターBリンク比率=(セクターAとBリンク数)/(セクターAの次数)
$$
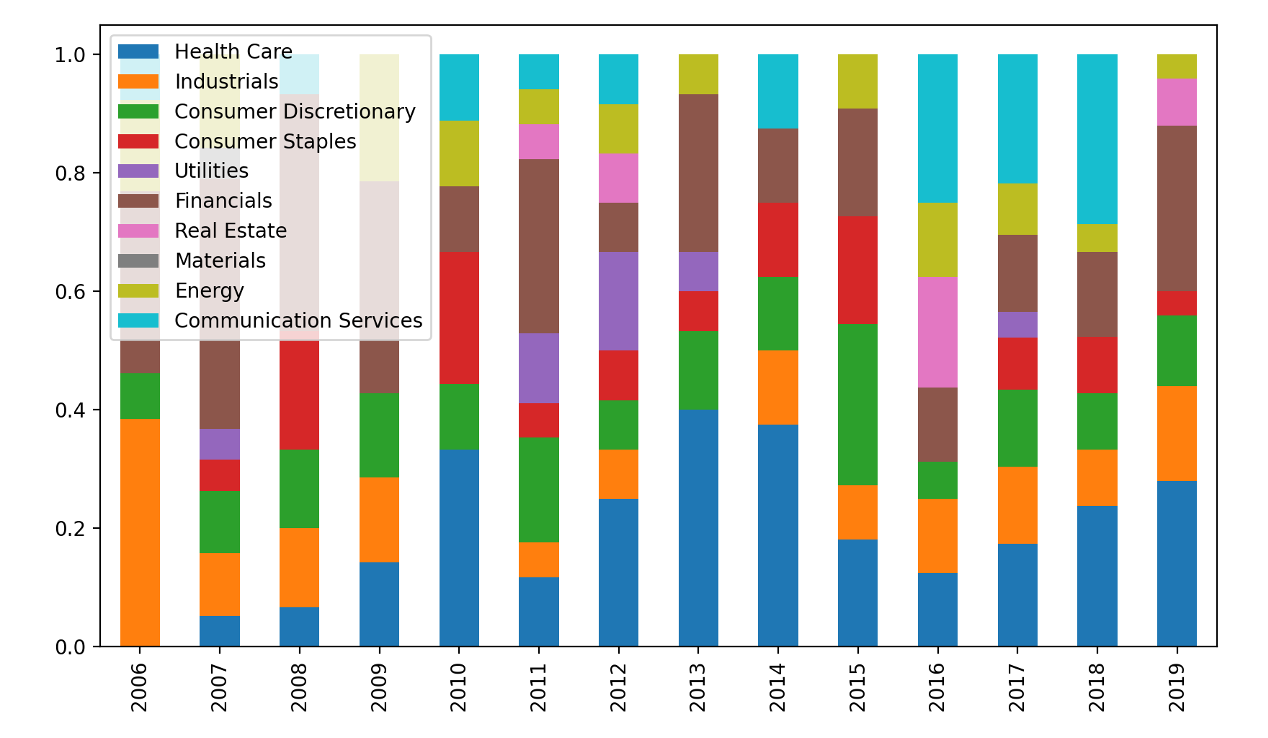
以上を踏まえ、前項で特性の変化が確認された2セクター(一般消費・情報技術)のリンク先セクター比率の推移を見ていく。
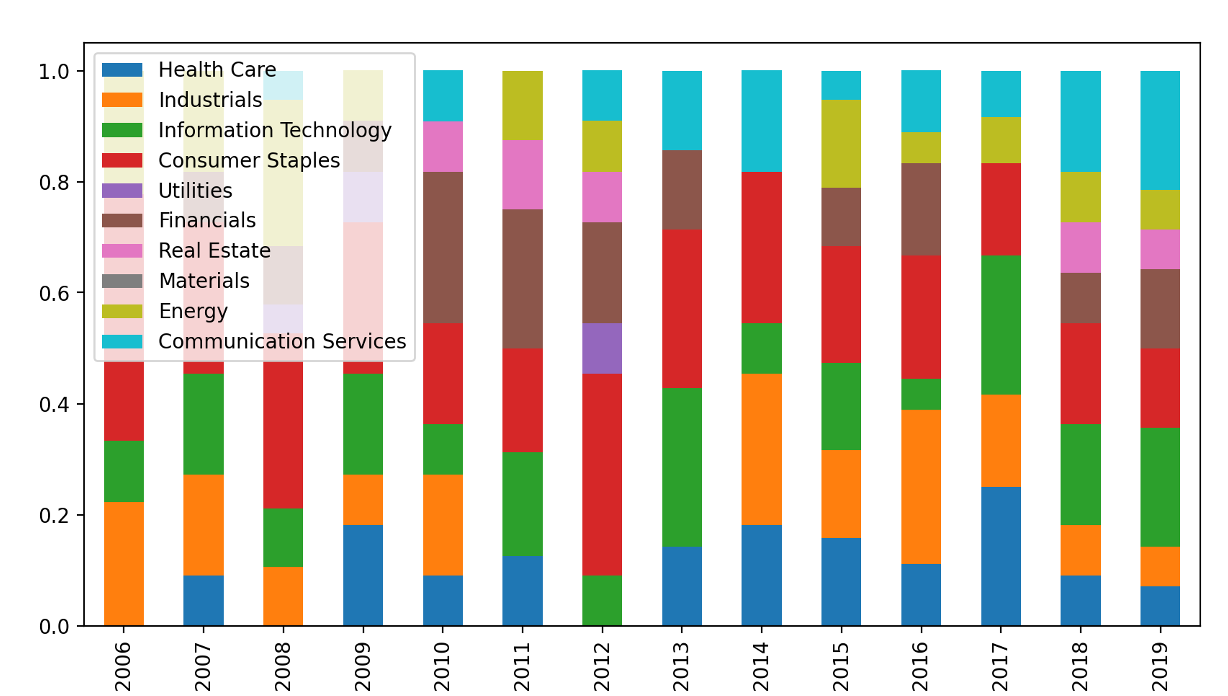
「情報技術」のリンク先セクター比率の推移
「一般消費」のリンク先セクター比率の推移
グラフより、いずれのセクターも長期的に見てヘルスケア(青字)、通信(水色)のセクター比率が徐々に上がっていることが分かる。
このことから、「一般消費・情報技術セクターは、ヘルスケア・通信といったディフェンシブセクターとの(ビジネス的な)関係性が高まったことで株価のディフェンシブ性が高まったのではないか」と考察される。
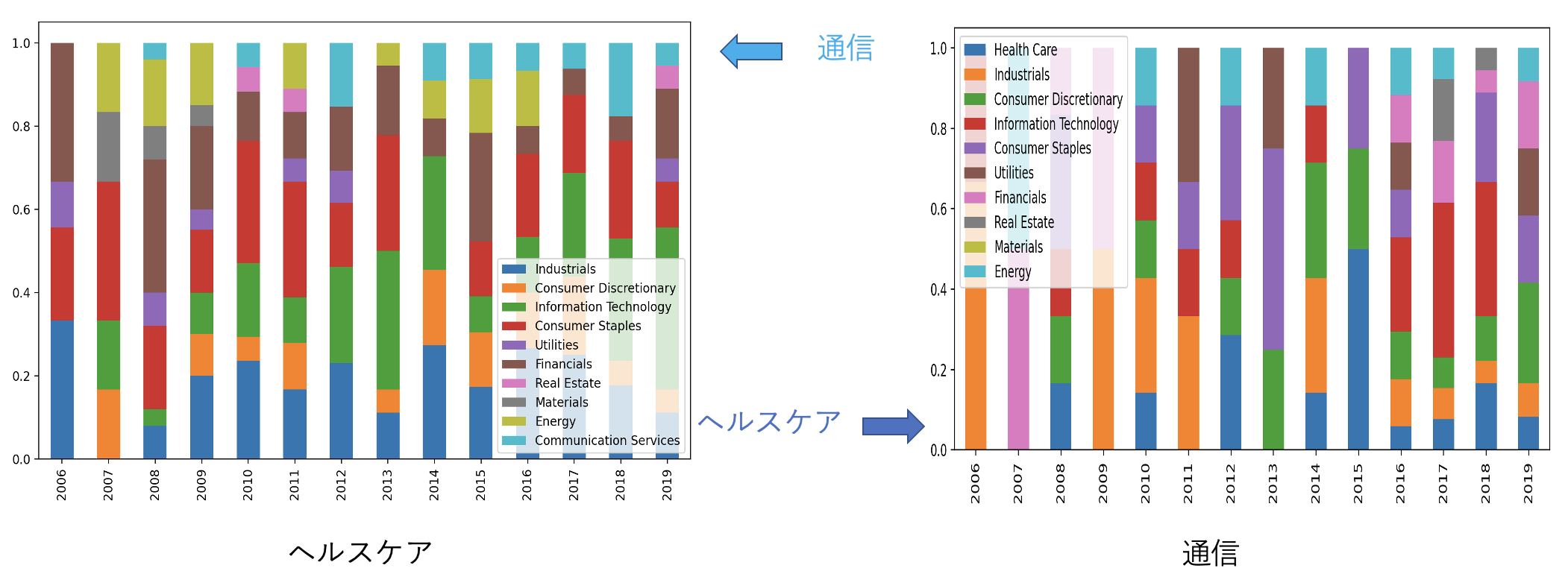
また以下、比率の高まったヘルスケア・通信セクターのリンク先の比率推移を見ると、「ヘルスケア・通信セクター間の関係性が高まっていること」が分かる。
「ヘルスケア」「通信」のリンク先セクター比率の推移
4-6. 結論
以上の分析から、以下2点の考察(仮説)が得られた。
- **情報技術・一般消費セクターは、ヘルスケア・通信セクターとの(ビジネス的な)関係性が高まったことで株価のディフェンシブ性が高まった、と考えられる。
- 1点目に加え、ヘルスケア・通信セクター間の(ビジネス的な)関係性が高まったことで、ヘルスケア・通信セクター(ビジネス的な)影響力が高まった、と考えられる。
4-7. 参考
参考までに、議論に挙げたセクターで実際にリンクが増加した銘柄は以下のような銘柄である。
- ヘルスケア⇨ギリアド、メルク
- 通信⇨グーグル、フェイスブック
- 情報技術⇨インテル、クアルコム
- 一般消費⇨アマゾン
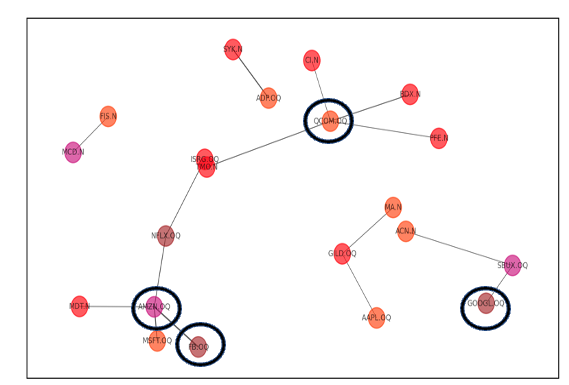
2019年のネットワーク(情報技術・一般消費セクター・ヘルスケア・通信の銘柄のみ)
☆実際に2019年頃、「GAFAMのヘルスケア市場への進出」が加速していたため(今もだが)、ぜひ新聞記事などで確認してみていただきたい。
5. 戦略一案
ネットワークによる可視化はあくまで足元の投資環境の確認や過去の構造変化の振り返りに用いることに適した1ツールであるため、アルファを狙う戦略を立てるには少なくともネットワーク単体で向かない、と考えている。
しかし、せっかく投資に関するモデルしたため、最後にネットワークを使った投資戦略の一案を紹介する。
詳細な説明は省くが、業種だけに着目したシンプルなLow Vlatility戦略の改良版として、ネットワークのディフェンシブセクターとのリンク数(予測値)に着目してウェイト付けすることを考える。
大雑把に言えば、
(ディフェンシブセクターとのリンク数の翌年予測値(単回帰))=(セクターウェイト)とするモデルである。
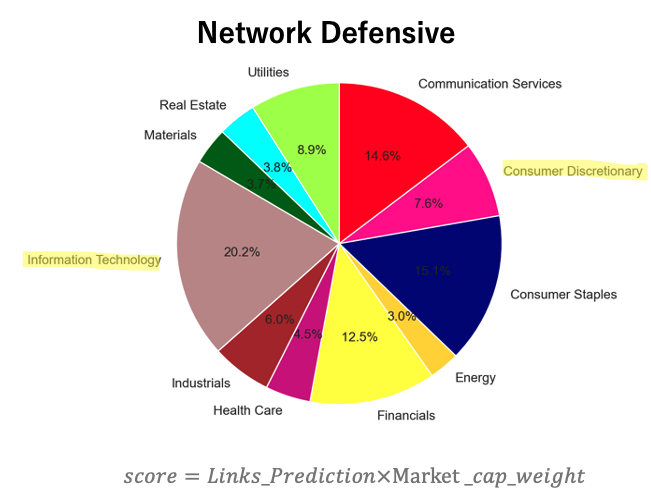
実際のポートフォリオは以下のようになる。
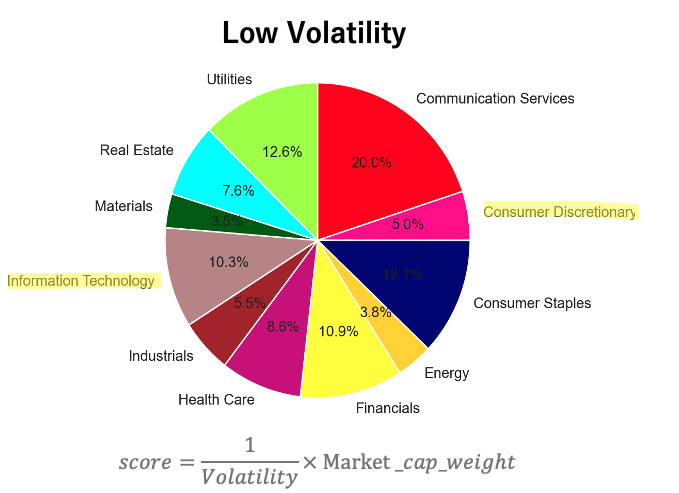
Low Vlatility戦略
Network活用戦略
一応、今回着目した一般消費・情報通信セクターの比率はLow Vlatility戦略より高くなった。
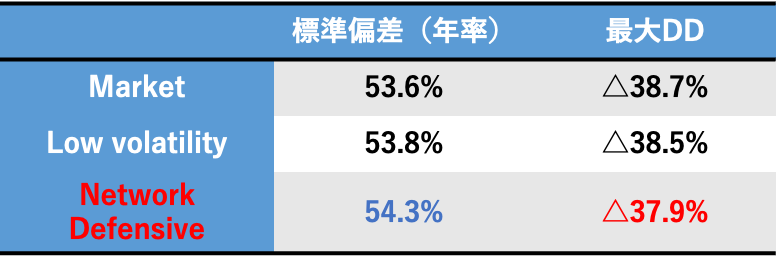
ディフェンシブ性を確認するため、2020年コロナショックのパフォーマンスを見ると以下のようになった。
コロナショック時のパフォーマンス
微妙な差ではあるが、標準偏差=リスク量は高まったものの、最大DDは微小に低下しており、一定のディフェンシブ性を確認できた。
5. 課題点と展望
- 考察を見てお気づきだろうが、今回ネットワークで可視化する手順を踏まずとも考察は可能だった。ただし、分析の起点とはなると考えるため、ネットワークとしたことでこそ把握できる情報を出力できるようにしたい。
- セクターごとにシクリカルorディフェンシブを分類したが本来その境界は曖昧で、銘柄ごとにより細かく見る必要がある。
- 今回は株式のみを対象に「セクター」を切り口にしたが、資産を債券・オルタナまで広げることも可能な上、色付けもファクターで塗り分けるなど、様々なカスタマイズが考えられる。
- こういった市場全体の構造変化は市場暴落などのシグナル検知で力を発揮できると考える。景気サイクルの転換などを視覚的に検知できたら大変興味深い。