【シグナル戦略】決定木を用いた株価の暴落予測

将来株価が暴落する企業を予測したい

※2022年2月時点の分析のため、分析期間や銘柄名などに違和感があるかと思われますがご容赦ください。

1. 目的

今回やりたいこと

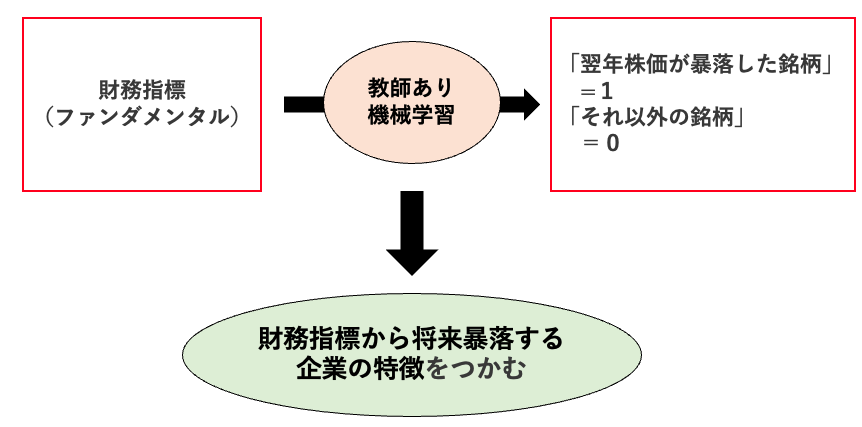
今回は、機械学習を用いて、「将来株価が暴落する企業の予測」を試みたい。
数年前より投資の世界でも機械学習を活用した戦略の立案がブームとなり、目的変数を株価リターンとした株価予測の研究を多く目にするようになった。しかし、こと金融市場においては、多くのノイズつまり再現性のない事象が含まれることから，データに過度にフィッティングしてしまう「過学習」が、株価予測において大きな課題となる。
そこで本研究では、目的変数を株価の連続データではなく、「将来の暴落の有無」とすることで，予め過学習を避けるようなモデル構築を目指す。その上で、定量的に相関関係を検証するだけにとどまらず、結果に定性的な解釈性を持たせることで予測の再現性を担保することも重視したいと考えたため、予測モデルには決定木モデルを用いた。

2. 決定木分析

2-1. 決定木モデルとは・・・

決定木モデル例

分析に入る前に決定木モデルの大枠について説明する。上に決定木モデルの出力例を示したが、決定木分析は、データをある条件に従って複数回分割することで，データの分類、または回帰する機械学習の手法であり、目的変数に対し、どの説明変数がどのような条件で効くのか直感的に理解しやすいことが特徴として挙げられる。
本研究では，分岐が必ず 2 分岐になることから特に解釈性の高い「CART (Classification And Regression Tree)」と呼ばれるアルゴリズムを用いる。CARTアルゴリズムでは，各ノード(サンプルの集合)$t$の乱雑さを表すジニ不純度$G(t)$を最小化していくことで決定木が構築される.
このとき、
$$
G(t)=1-\sum_{i=1}^c\frac{n_i^2}{N}
$$
ただし、$c$は目的変数のクラス数（今回は２）、$N$は集合内の全サンプル数，$n_i$はクラス$i$に属するサンプル数である。
要するに、分岐によって得られる利得（Gain）$\Delta{G(t)}$を最大化する説明変数と閾値を随時決定していく。
このとき、
$$
\Delta{G(t)}=G(t)-w_LG(t_L)-w_RG(t_R)\
$$
ただし、$t_{LR}$はそれぞれ左右の分岐後ノード、$w_{LR}$はそれぞれ左右の分岐後ノードの分岐前ノードに対するサンプル数の割合である。

2-2. 枝刈り

決定木分析において汎化性能を得るためには、木の深さを一定基準まで制限する「枝刈り」をすることで木の深さを制限する必要がある。なぜなら、もし枝刈りせず分析を行った場合、訓練データに過剰に適合してしまい、新しいデータに対するモデル性能が低くなってしまうためである。一方で、枝刈りをしすぎてしまうと、そもそもの予測性能が落ちるため、適切な木の深さを予め決定しておくことが、決定技モデル構築においては重要である。

2-3. 交差検証

今回、木の深さを決定するための汎化性能評価には、「交差検証(Cross varidation)」と呼ばれる手法を用いる。$k$-分割交差検証では、検証に用いるデータを$k$個に分割し、その内一つをテストデータに残りの$k-1$個を訓練データとして使い、訓練データを学習した決定木の汎化性能をテストデータを用いて評価する。これを$k$個のデータが全て一回ずつテストデータになるよう、$k$回学習を行って評価指標の平均を取る。今回は、木の深さを2から6まで変化させ、それぞれの設定においてデータを5分割（$k=5$）することで汎化性能を評価する。
このとき、評価指標は以下のものを使用する。

評価指標

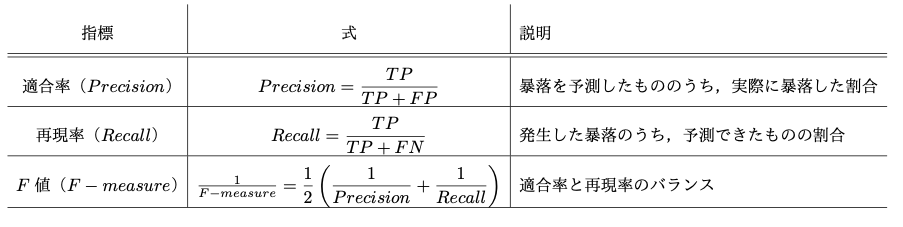
ただし、TP(True Positive）は真陽性つまり暴落を予測して翌年暴落した回数、FP(False Positive)は偽陽性つまり暴落を予測して翌年暴落しなかった回数FN(False Negative )は偽陰性つまり暴落しないと予測して翌年暴落した回数である。
※本研究では目的変数のラベルの割合に大きな偏りがある（暴落は全体では稀）ため、上記評価指標を使用することとする。

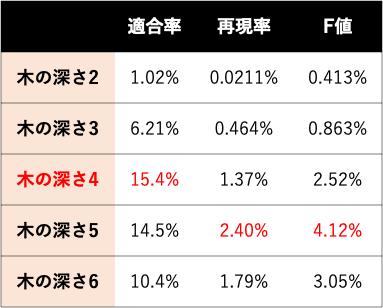
以上の評価指標を用いて、木の深さごとに決定木の汎化性能を検証した結果が以下の表の通りである。

木の深さに応じた汎化性能

表より、適合率においては木の深さが4の場合に最大値をとるが、再現率においては木の深さが５の場合に他の条件と比べ特に優れた結果となり、両者のバランスを測るF値においても深さが5の場合に最大値をとる。これらの結果を考慮すると、本モデルでは木の深さを５に制限することが自然であるように考えられる。しかし、本研究の主目的は「起こりうる暴落を多く当てること」より「的中率の高い暴落の予兆を捉えること」としたいと考え、（１）適合率を重視したモデルが適している。また、予測力以上に説明力を重視するため、（２）定性的な解釈が困難な木の深さが5以上の決定木はモデルの趣旨にそぐわない。．以上2点の理由から、総合的な汎化性能ではやや劣るものの、高い予測精度と解釈性が期待できる 「木の深さが4の決定木」で検証していくこととする。

3. 分析概要

それでは、実際に暴落予測の分析に移っていく。
分析条件は以下の通りである。

【分析条件】

• 分析対象：米国株、S&P500全銘柄（2020年4月末時点）
• 分析期間：2006年11月末〜2020年4月末（教師データは〜2015年7月末）
• 暴落の定義：暴落$\Leftrightarrow$翌年の銘柄リターン$<-3\sigma$
• 入力ファクター（説明変数）：以下一般的に使用される８ファクター
  

※このとき入力ファクターには、クロスセクションの特徴量の位置付けを把握しやすくするため、「標準化」と呼ばれるデータのスケーリングを施している。
銘柄$i(i=1,\dots,n)$の特徴量$x_i$に対する標準化の定義は以下の通りである．
$$
z_i=\displaystyle\frac{x_i-\mu}{\sigma}. \
$$
ただし，$\mu$，$\sigma$はそれぞれ時価総額加重の平均，標準偏差であり，銘柄$i$の時価総額加重比率$w_i$を用いて，以下のように表される。
$$
\mu=\sum_{i=1}^{n}w_ix_i,  
\sigma=\sqrt{\sum_{i=1}^{n}w_i(x_i -\mu)^2}.\
$$

※暴落の定義をZスコアで表すと、暴落$\Leftrightarrow$$z_i<-3\sigma$

4. 分析結果

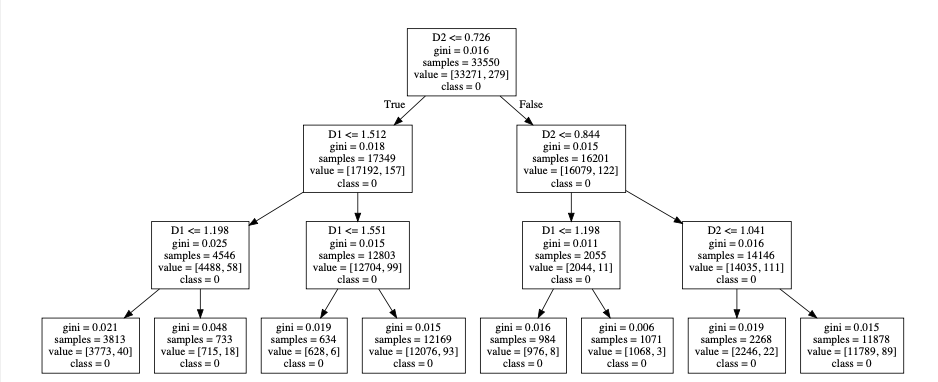
前節で記載した条件の下、構築した決定木の出力が以下の通りである。本来、予測精度を高めることを目的とする場合、複数の決定木を作成し結果を集約するのが正攻法だが、今回は「結果に定性的な解釈性を持たせること」にも重きを置いているため、単一の決定木から暴落につながる予兆を捉えていくこととする。

学習結果の決定木

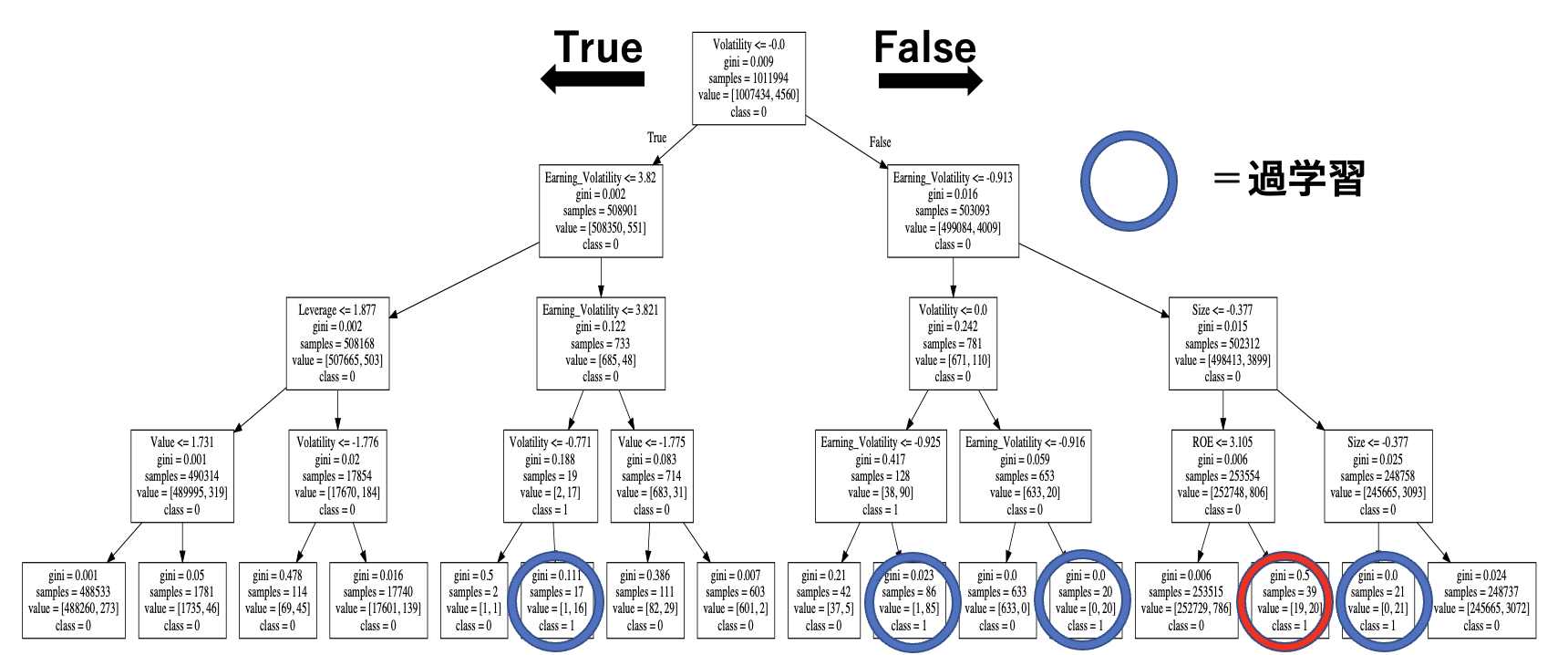
改めてとはなるが、決定木は樹形図のような形で表現され、CART アルゴリズムにおいては各ノードの命題に対する真偽に応じて2 方向に分岐していく。一連の二者択一を繰り返すことで，最終的には最終ノード(葉)の暴落か否か(1か0か)の判別に至る。

青丸は過学習

上の図においては，暴落に属する葉をあえて分かりやすく丸で囲っている。暴落に属する葉は全部で5枚あることが分かる。
ただし、その内の4枚にあたる青丸で囲われた葉は、視覚的にではあるが「過学習」と判断した.例えば，一番左の丸で囲われた葉に至るパスを確認すると、2つ目の分岐と3つ目の分岐条件を組み合わせると、暴落の条件が，3.82 <Earning Volatility< 3.821 となってしまう。これは，訓練データの極小さな区間の値に過剰に適応していることになり、この予測の汎化性は非常に低いと考えられる。その他3つの葉に至るパスについても同様の特徴がみられる。
よって、残る赤丸で囲った葉に至るパスについてのみ、真に暴落に対する予測力を持つ可能性がある。したがって、赤丸で囲った葉に至るパスを詳細に分析し、それらの条件が実際に予測力を有するか、を次節以降で検証していく。

4. 検証

4-1. 赤丸に至るパスにフォーカス

上の全体図では、個別のノードがよく確認できないため、以下に赤丸の葉に至るまでのパスにフォーカスを当てて表示する。

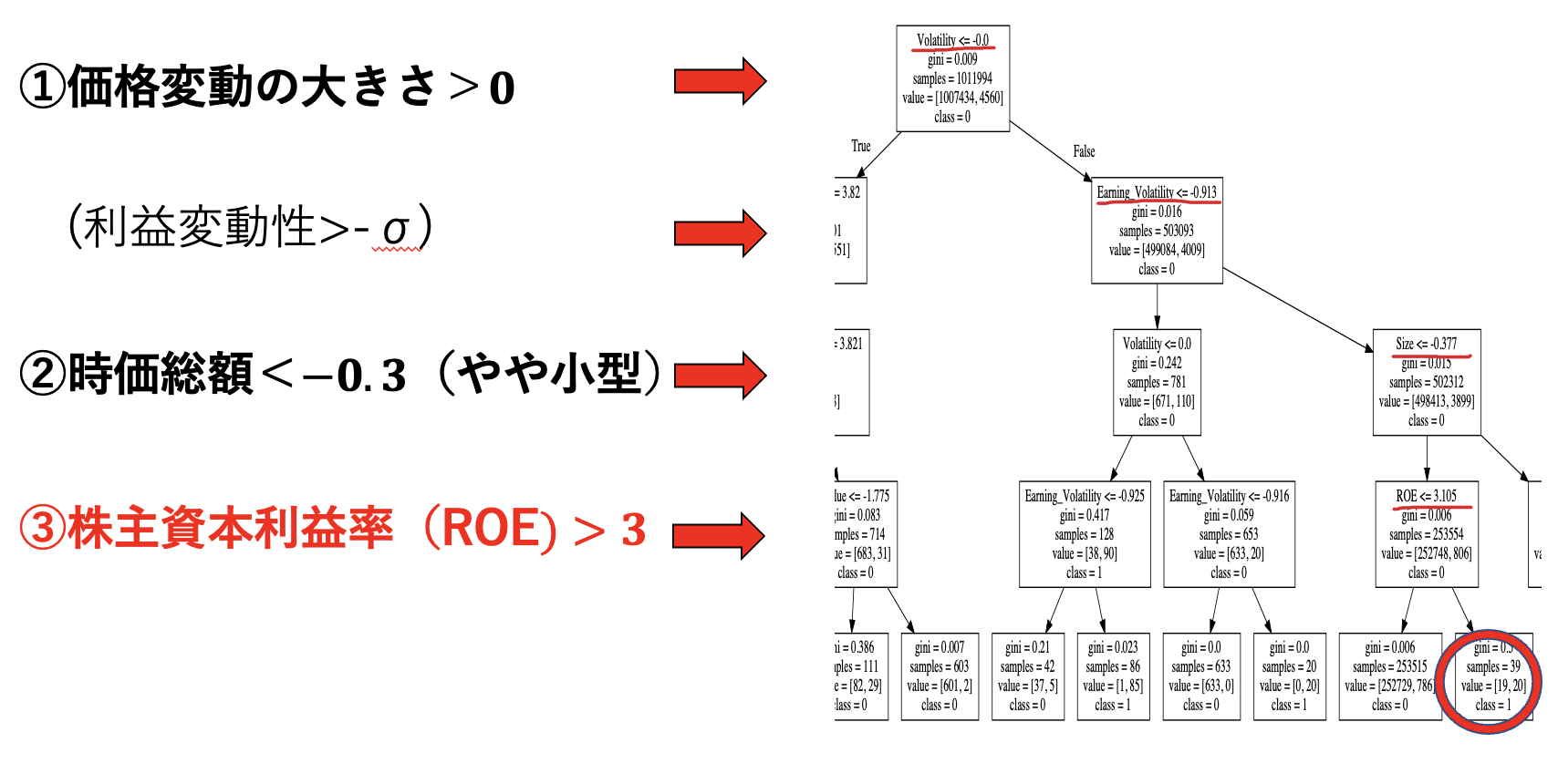
黒丸で囲った葉に至るパスは4つの分岐によって構成され、それぞれの分岐において異なる特徴量が用いられている。つまり、「4つのファクターで構成されるそれぞれ4つの条件を全て満たすサンプルが翌年暴落につながりやすい」と解釈すればよい。既に上図でも記載しているが、本研究では、暴落との因果関係に定性的な解釈を持たせたいため、4つの条件の端数を削るなどして、よりシンプルな3つの条件にまとめた。

　　条件（１）　Volatility（価格変動の大きさ）>0
　　条件（２）　Size（時価総額）<-0.3
　　条件（３）　ROE（株主資本利益率）>3

※各特徴量は標準化により、およそ平均 0 分散 1 の標準正規分布に近似してあるため、例えば ROE> 3 は，ROE がクロスセクション平均よりおよそ 3σ 以上高いことを意味する。

4-2. 更に条件（３）にフォーカス

続いて、条件（１）〜（３）の暴落予測力を検証したいところだが、今回はさらに条件（３）にフォーカスを当てたい。
条件(1)、条件(2)はそれぞれ価格変動の大きさ、時価総額で表現され、株価のボラティリティは一定の自己相関をもつこと、時価総額の小さい小型企業は財務基盤が安定していないことなどから、これらの条件を満たす企業が将来暴落につながりやすいことは直感的な理解に沿っている。しかし、条件(3)で用いられROEという投資指標は、投資家が投下した資本に対し企業がどれだけの利益を上げているかを表す指標として、一般にROEの数値が高いほど経営効率が良いとされていることから、「ROE(株主資本利益率)> 3、すなわち ROEが異常な高まりをみせた場合、企業株価が暴落しやすい」という結果は、そうした ROE に関する通説とは一見して反している。
以上から、機械学習から導き出された条件（３）の結果は興味深く、まず焦点を当てたいと考えた次第である。条件（３）の暴落予測力を検証するため、まずはROEと将来リターンの関係性について見ていく。

ROE（標準化）、翌年累積リターン（標準化）の散布図①

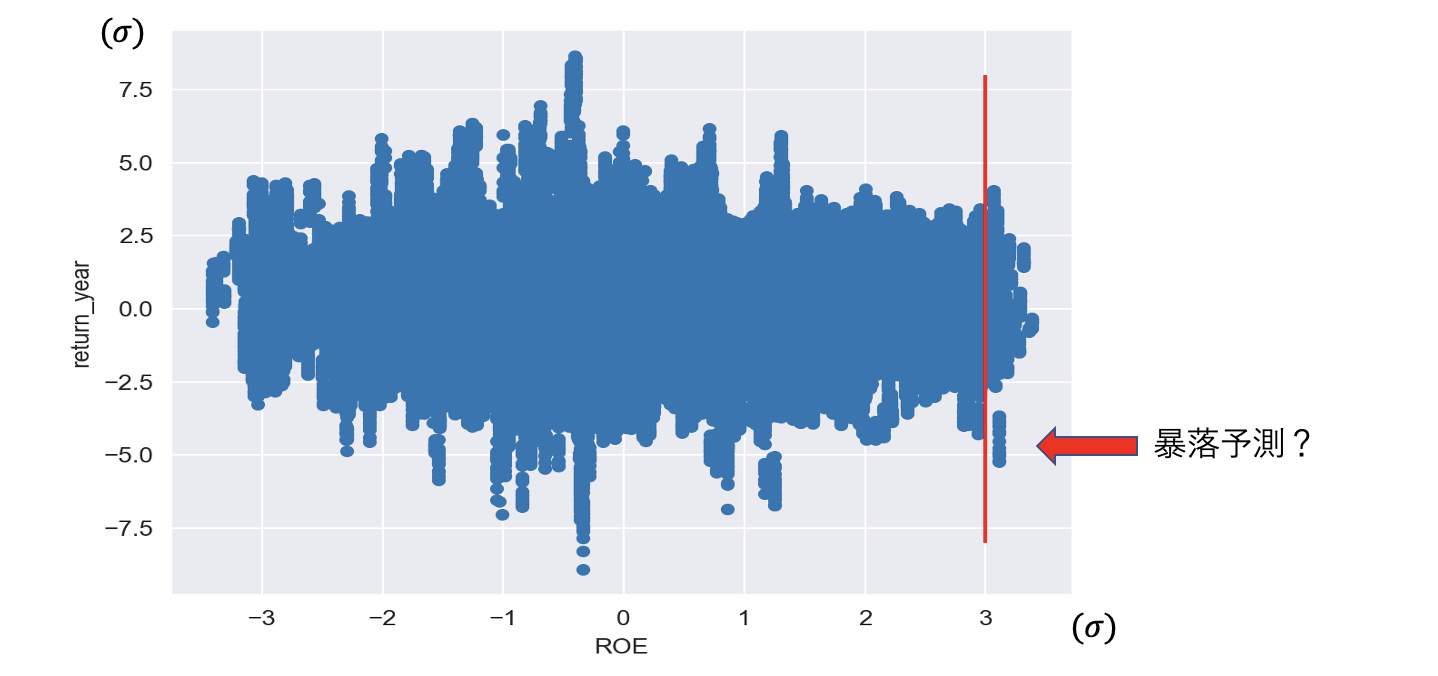
上図では、横軸を標準化したROE、縦軸を標準化した翌年の累積リターンとして検証期間の全サンプルをプロットした散布図を作成し、ROE= 3 の赤線を境界として加えている。
一見して、ROEと翌年のリターンに相関関係は見られないが、ROE>3、つまり図の直線より右側の領域に小さなクラスターのような点の集合が確認できる。クラスターは標準化した翌年の累積リターンが3以下の高さに密集しており、これが条件（３）が示す暴落予測だと推察される。
さらに、より視覚的に分かりやすいよう、ROE$<3$を満たすサンプル群とROE$>3$を満たすサンプル群それぞれについて、標準化した翌年の累積リターンをヒストグラムで表示する。

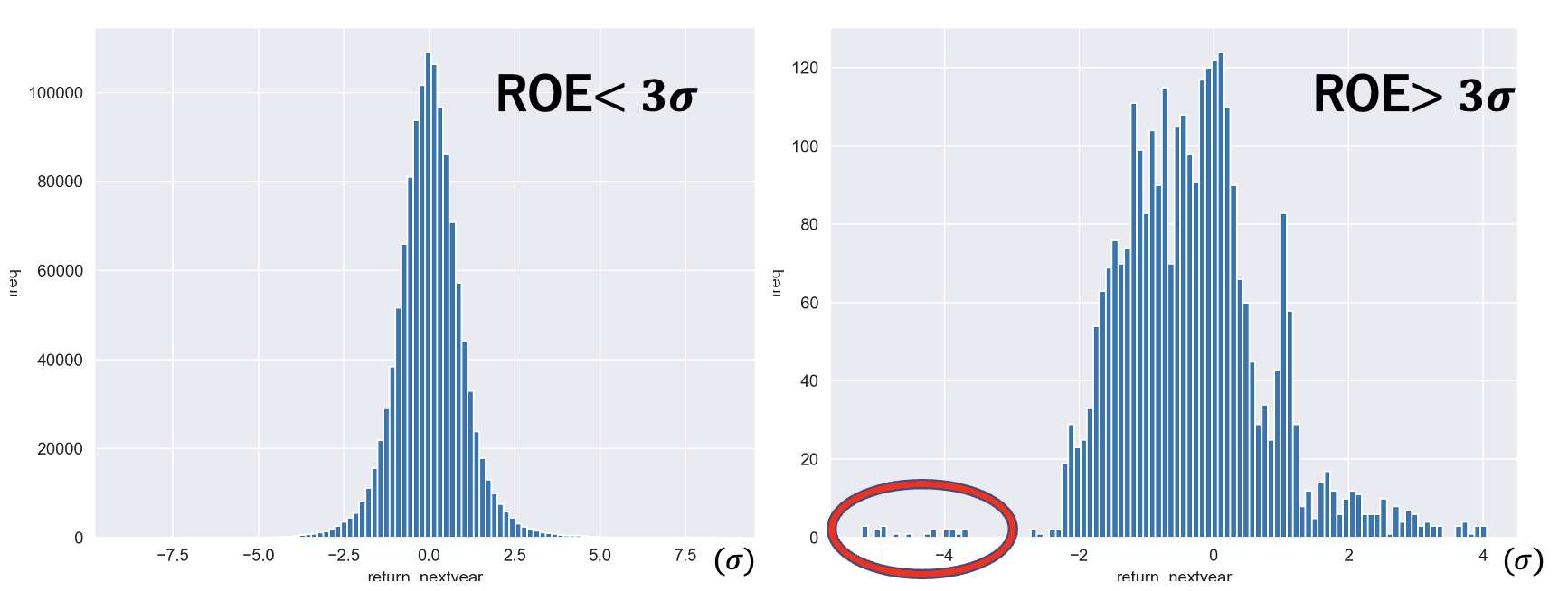
翌年累積リターン（標準化）のヒストグラム①

ROE<3の場合のヒストグラムの形状が正規分布に近いものであるのに対し、ROE>3の場合は 、左側（負の方向）に裾が広がっていることがわかる。サンプル数が少ないため信頼度は決して高くないが、ROE<3の場合と比べROE>3の場合、翌年の累積リターンの期待値は大きく変わらないが、翌年大きな下落が発生する確率が高まることが確認できる。
さらに、定量的な側面から検証した結果が以下である。標準化した翌年の累積リターン−2、−3、−4 を下回る確率を、それぞれ通常時とROEが３を下回った時の２パターンで比較した。

大幅な下落の発生確率①

表より、ROE>3を満たした場合、本研究における暴落の定義「（標準化した翌年の累積リターン）<-3」が発生する確率は、何も条件を課していない全体の発生確率と大きく変わらない。（1.46倍）ただ、暴落の閾値が-4、つまり「より大きな下落」が発生する確率は、何も条件を課していない通常の発生確率と比べ5.28倍と大きく上昇する。
ここでもサンプル数の問題があるものの、条件（３）は本研究の定義に沿った「暴落」に対する予測力を有してはいないが、標準化した翌年の累積リターンが$-4$を下回るような 「大暴落」に対する一定の予測力を有していることが分かった。

4-3. 改めて条件（１）〜（３）を検証

前節で条件（３）が大きな株価下落に対して一定の予測力を持つ可能性を示したが、ここで改めて決定木の結果によって導き出された条件（１）〜（３）の暴落予測力、すなわち条件（１）（２）を組み合わせることで予測力が向上するかを検証していく。検証方法は前節と同様である。
※念の為条件（１）〜（３）を再掲する。

　　条件（１）　Volatility（価格変動の大きさ）>0
　　条件（２）　Size（時価総額）<-0.3
　　条件（３）　ROE（株主資本利益率）>3

ROE（標準化）、翌年累積リターン（標準化）の散布図②

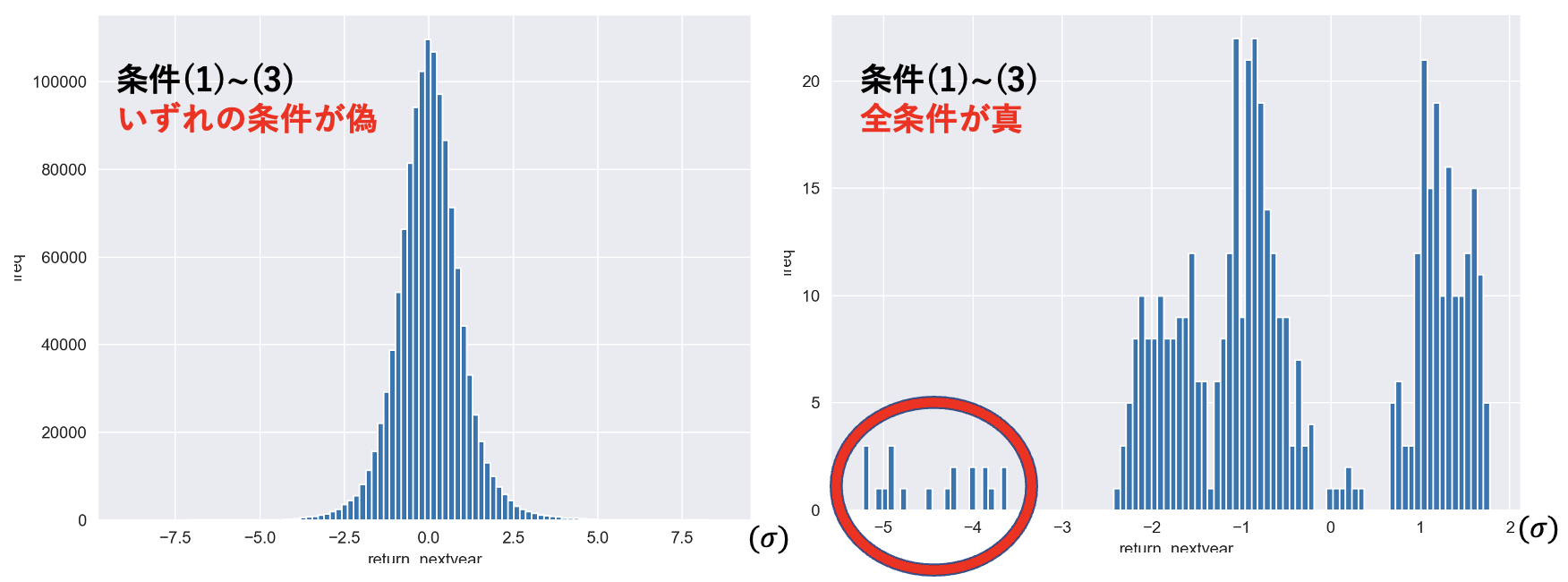
前節同様、条件（１）〜（３）が全て真のサンプル群についてはヒストグラムの形状が正規分布に近いものであるのに対し、条件（１）〜（３）の少なくとも一つが偽であるサンプル群については左側（負の方向）に裾が広がっていることがわかる。ただ前節と比べ、条件（１）〜（３）が全て真のサンプル群についてはグラフがかなり左に偏り、左側の裾が相対的に広がっていることが分かる。
さらに前節同様、定量的な側面から検証した結果を示す。今回は、それぞれ通常時と条件（１）〜（３）が全て真の時の２パターンで比較した。

大幅な下落の発生確率②

一番右の列をご覧になって分かる通り、条件（１）、（２）を加えると、通常時と比べたときのリターンが大幅に下落する（２σ、３σ、４σ以上の下落）確率が大幅に上昇していることが分かる。
より分かりやすいよう、先ほどの条件（３）のみの場合と比較して記載する。

大幅な下落の発生確率①＋②

表より、条件（３）のみでは、本研究の暴落の定義「（標準化した翌年の累積リターン）$<-3$」が発生する確率は、何も条件を課していない全体の発生確率と大きく変わらなかったが、条件（１）（２）を加えると、暴落の発生確率は通常と比較して11.2倍、閾値を-2とした場合でも、6.63倍と大きく上昇している。また、標準化した翌年の累積リターンが-4を下回るような「大暴落」に対する予測力も、条件（３）のみの場合の5.28倍と比べ、40.8倍と大きく上昇した。これは、保有する株式銘柄が条件（１）（２）（３）を満たした場合は、通常時と比べ資産価格が$4\sigma$以上下落する確率が４０倍以上も高まることを意味する。

以上をまとめると、「ROEの異常な高まり」は、標準化した翌年の累積リターンが$-4$を下回るような「大暴落」に対する一定の予測力を持つが、そこに「価格変動の大きさ」、「時価総額」に関わる条件を加えることで、本研究の定義に沿った「暴落」に対して高い予測力を発揮することが分かった。

※繰り返しになるが、条件（１）（２）（３）を満たすサンプル数はかなり限られるため、その分結果の信頼度も低下していることには留意が必要である。

5. 考察

5-1. そもそもROEとは・・・

最後に、前節までで検証行った、決定木によって捉えた暴落の予兆について、定性的な解釈を考えていきたい。
そもそもROEとは、投資家が投下した資本に対し企業がどれだけの利益を上げているかを表す指標であり、投資家の立場に立てば、ROEが高いほど投下した資本に対する利益の還元が大きい企業だと捉えることができる。ただし、「高ROE企業は期待リターンが高い」と短絡的に考えることにはいくつかの問題点があり、その一つが米国の化学会社デュポン(Du Pont)が開発した、デュポン分解によって指摘される。デュポン分析によると、ROEは以下のように３つの要素に分解される。

\begin{eqnarray*}
\rm{ROE}
&=&\displaystyle\frac{当期純利益}{売上高}\times\frac{売上高}{総資本}\times\frac{総資本}{自己資本}\\
&=&\displaystyle{売上高純利益率}\times{総資本回転率}\times{\textbf{財務レバレッジ}}
\end{eqnarray*}

ここで重要になるのは、3つ目の「財務レバレッジ」である。財務レバレッジは自己資本比率の逆数で示され、総資本に占める負債の割合が高いと財務レバレッジは高まる。つまりROEは、単に利益効率を高めるだけでなく、負債（借金）をテコにしてレバレッジ効果を効かせることで向上させることができる。

5-2. ROAとは・・・

ここで、ROEとよく似た「ROA（総資産利益率）」という指標を導入する。ROAは、ROEと違い分母が総資産で表されることから、以下のように分解される。

\begin{eqnarray*}
\rm{ROA}
&=&\displaystyle\frac{当期純利益}{売上高}\times\frac{売上高}{総資本}\\
&=&\displaystyle{売上高純利益率}\times{総資本回転率}。
\end{eqnarray*}

ROEの式と比べてわかるように、ROAはROEを財務レバレッジで割ったものと考えてよい。すなわち、「高ROEかつ低ROAの銘柄は高い財務レバレッジがかかっている」と解釈することができる。

5-3. 暴落を予測したサンプル群のROAを確認

それでは、前章までの検証で暴落を予測したサンプル群のROAはどのくらいだったのか。（つまり財務レバレッジはどのくらいかかっていたのか）以下は、条件（３）のみ、及び条件（１）（２）（３）全てを満たすサンプル群それぞれについて、ROAをヒストグラムの形で表したものである。

ROA（標準化）のヒストグラム

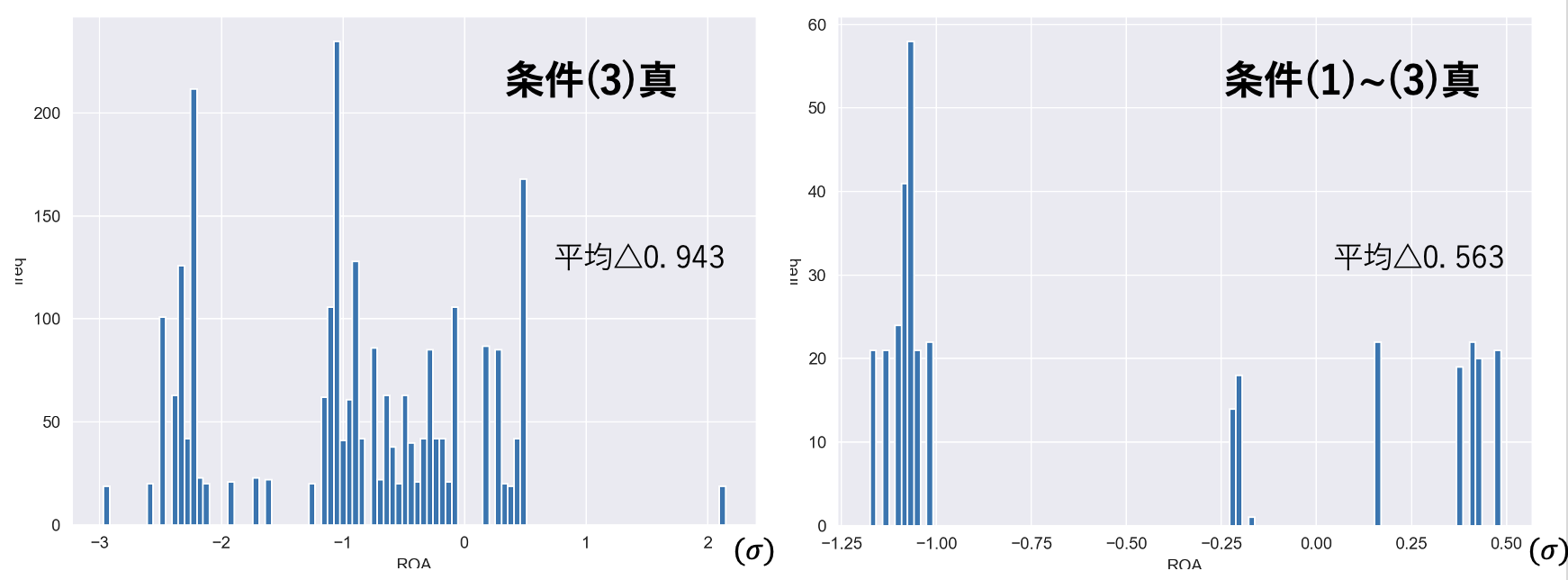
どちらのサンプル群も、ヒストグラムの山が左（負の方向）に偏っていることがわかる。また、標準化したROEがいずれも３を超えているにも関わらず、標準化したROAの平均はそれぞれ負の値であり、極めて高いROEに反して、ROAは時価総額加重平均を下回る水準であった。
以上より、以上より、ROEが平均より$3\sigma$を超える企業の多くは、財務レバレッジ（借金）をテコにして一時的に投下資本に対する高い利益率を実現したものの、それにより財務の健全性が悪化し、翌年暴落、またはそれに近い株価の下落につながったものと推察される。

5-4. 個別銘柄を見ると・・・

実際、検証期間内に条件（１）（２）（３）を全て満たした個別銘柄の一部を取り上げると、財務レバレッジの上昇が大きな下落につながったことが確認できる。

<1>
例えば、半導体会社のアドバンスト・マイクロ・デバイセズ（AMD）は2011年11月11日に上の３条件を満たし、翌年$\Delta$100.8%（市場平均+16.5%）と大きく下落した。このとき、AMDは劇的な性能向上が見込まれる新製品の開発を発表したものの、その後、その新製品が競合であるインテルの製品に劣後してしまったことより投資家の失望を買い、大きな下落が起こったとされている。つまり、製品開発に多くの資金が必要となり一時的に財務レバレッジが大きく上昇し、財務リスクが高まったことが暴落につながったと考えられる。

<2>
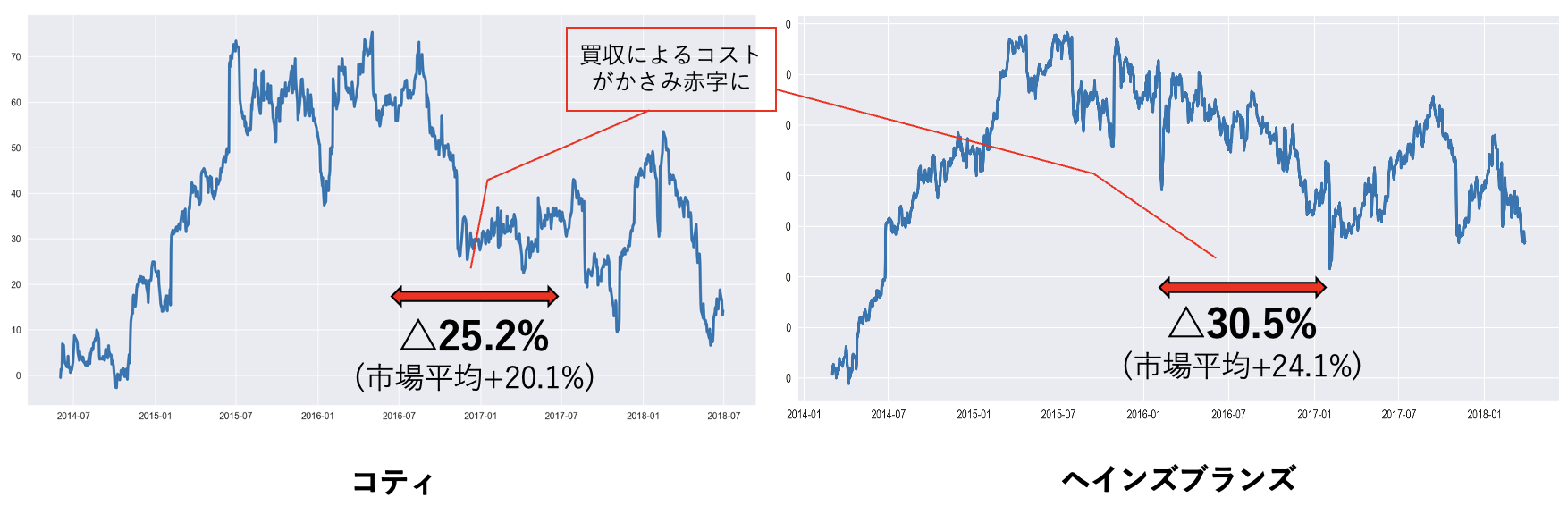
もう1銘柄を例にとると、衣料品メーカーのヘインズブランズ（HBI）は2016年3月3日に条件を満たし、翌年$\Delta$30.5%（市場平均$+24.1%）と暴落に近い下落が起こった。この年、HBIは合計10億ドル規模の大型買収を行ったもののの、その後実店舗での収益が失速し買収のコストをカバーしきれなくなったことが、株価急落につながったとされている。ここでも、大型買収によって財務レバレッジが上昇し、財務リスクが高まったことが急落に寄与したと考えられる。

6. 課題点と展望

• 今回は、「結果に定性的な解釈性を持たせること」にも重きを置いたことから、単一の決定木を選んだが、投資家の立場で考えると、定性的な理由づけがあるからといって、１回のテストで出てきた結果を当てにして投資することは不安に思える。理想的には、ランダムフォレスト・ニューラルネットなどを活用し予測力を担保しつつ、一定の解釈性を与えたいところである。
• この研究では、「過学習を防ぐために暴落か否かの２択を正解に置いた点」が肝ではあるが、暴落という事象はサンプル数が少なくなり、再現性を保証できないことが大きな難点であることに気が付いた。過学習とサンプル数の確保のバランスという点で、暴落の定義づけの点でもう少し検討の余地があったと思われる。
• 今後、機械学習の活用において、回帰問題を分類問題にすり替えることで過学習を抑制する、という手法はまだまだ活用の余地があると思われる。どういった条件が揃うとどういったリスクイベントが起こるのか、を考える際、アイデアの起点として機械学習を使い、市場に隠れる様々な「パターン」を洗い出すことで、機械学習を実用的なツールとして今後も活用できるのではないかと考える。