統計学入門8.2をPythonで解く試み

#概要
統計学入門の問8.2の2番(p173)の問題をPythonにて解きます。

8.2<ランダム・ウォーク>　確率変数X1,X2,…,Xnは独立で,確率分布
P(Xi=1)=p, P(Xi=-1)=q (i=1,2,...,n)
に従っている.ただしp=1-q.

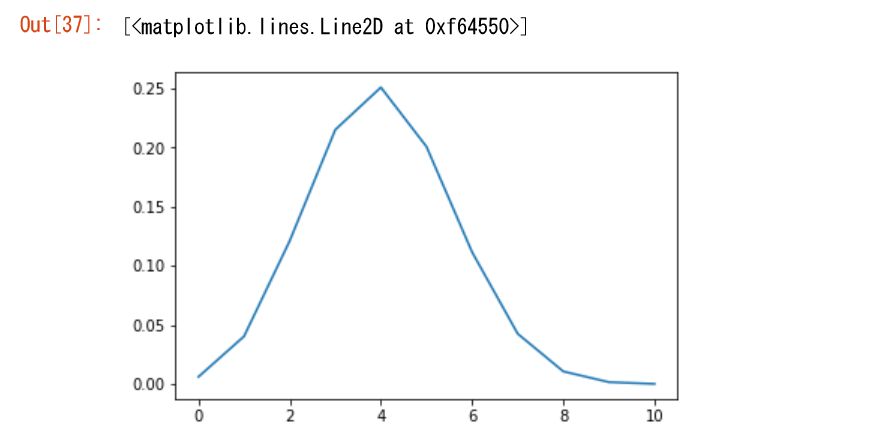
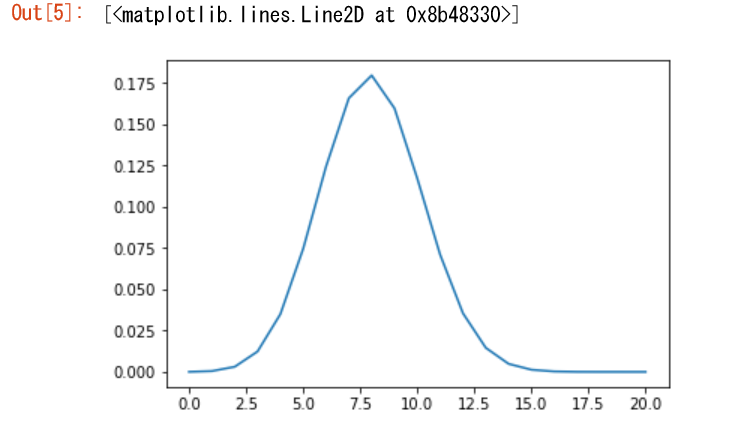
p=0.4の時,X1+X2+...+X10,X1+X2+...+X20の近似的確率分布をグラフにせよ。

#環境

Jupyter notebookを用います。

#ソースコード

code

import numpy as np
import matplotlib.pyplot as plt
from sympy import *

def ranwal(k):
    ans=factorial(10)/(factorial(k)*factorial(10-k))*(0.4**k)*(0.6**(10-k))
    return ans #関数を設定

def data():
    result=[]
    for k in range(11):
        result.append(ranwal(k))
    return result #0~10の間で回す
plt.plot(data())

code2

import numpy as np
import matplotlib.pyplot as plt
from sympy import *

def ranwal(k):
    ans=factorial(20)/(factorial(k)*factorial(20-k))*(0.4**k)*(0.6**(20-k))
    return ans #関数を設定

def data():
    result=[]
    for k in range(21):
        result.append(ranwal(k))
    return result #0~20の間で回す
plt.plot(data())

#結果
以下のようなグラフを得ました。

間違い等あればご一報ください。

#参考文献
統計学入門(東京大学出版会)