統計学入門9.6をPythonで解く試み

概要

統計学入門(東京大学出版会)の練習問題9.6の2番をPythonにて解きます。
問題は以下の通り。

あるデパートの注文服売り場の販売員の所へ来る一時間当たりの来客数は,λ=1.5のポアソン分布に従うという。午前3時間の来客数が5人以上である確率を求めよ。

考え方

• λ=1.5とは、「一時間当たりの来客数が平均1.5人である」ことを言います。
• ポアソン分布は再生性を持ちます。再生性とは、「独立な複数の確率変数が同一の分布に従うとき、その和もそれらと同じ分布に属する」ことを言います。
• 対して、母集団分布がいかなる分布であっても、そこから取り出した標本の数が多ければ、それら標本の総和は正規分布になります。これを中心極限定理といいます。
• 今回は標本の数が小(たった3つ!)なので、中心極限定理は使えず、従って「一時間当たりの来客数を確率変数Xとみなし、三時間の来客数をX1+X2+X3で表現する」という方針で行きます。

環境

Jupyter notebookを用います。

#ソースコード
以下のようになります。

code.rb

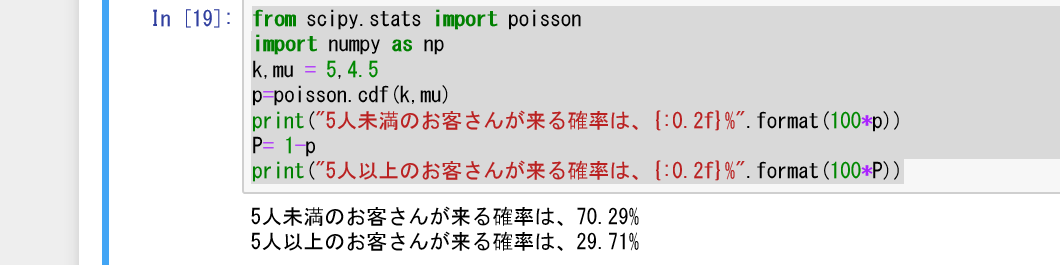
from scipy.stats import poisson
import numpy as np
k,mu = 5,4.5
p=poisson.cdf(k,mu)
print("5人未満のお客さんが来る確率は、{:0.2f}%".format(100*p))
P= 1-p
print("5人以上のお客さんが来る確率は、{:0.2f}%".format(100*P))

#結果
以下のような結果となりました。

間違い等あればご一報ください。