本記事は,ニューヨーク州立大学バッファロー校准教授の増田直紀氏と一緒に書きました.
概要
2018年平昌オリンピックの女子マススタートで髙木菜那選手が金メダルを獲得しました.本記事では,マススタートで勝つために有効な戦略についてデータ解析を行った我々の論文 [1] について簡単に解説します.
我々の結果を一言でいうと,レース終盤まで誰かの後ろに隠れて上手く空気抵抗を減らすような選手がマススタートでは勝つ傾向にあるということです.
では,詳しい中身について見ていきましょう.
データ
我々はYouTubeのデータを用いました.YouTubeにアップされている,国際スケート連盟(ISU)のW杯の2シーズン(2016/2017と2017/2018)分のマススタートレースが分析対象です.マススタートでは,1周400mのトラックを16周($=$ 6,400m)して順位を競います.分析したレースの1つである,2017/2018シーズンにソルトレイクシティで行われたマススタート男子決勝のYouTubeビデオはこちらです.我々が使用したレースのYouTubeリンクはGitHubに上げてあります.分析したのは全部で14レースですが,そのうち5レースでは一部の選手がレースの序盤または中盤で大逃げを打って勝ったので,これら5レースを除いた9レースを分析しました.
結果
中間順位はゴールに近づくにつれてどうなるか?
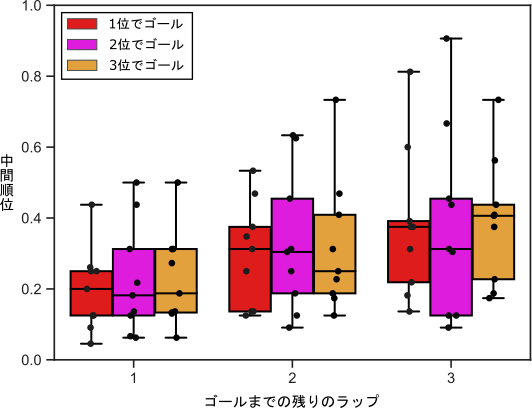
中間順位,ゴールまでの残りのラップ(周),3位以内にゴールした選手のゴール順位の3種類のデータの関係性をグラフにしたものが以下の図です.
横軸はゴールまでの残りラップです.残り3,2,1周を見ています.縦軸は中間順位です.中間順位は,ゴールまでの残りラップが3,2,1周になった時点での順位のことです.レースごとに出場選手数が異なる(標準は24人)ので,値を正規化しました.つまり,先頭の選手の順位は縦軸の0に近くて,最後尾の選手の順位は1に近いということです.3つの縦棒はゴール順位を箱ひげ図で示したものです.各点が,1つのレースの1人の選手にあたります.
この結果から何が分かるでしょうか? 残り3周,2周,1周となるにつれて,点群が全体的に下がっています.これは,最終的に3位以内でゴールした選手たちが,ゴールに近づくにつれて徐々に前の方に出てくることを示しています.この結果は,線形混合モデルを用いた統計的検定でも有意でした.
誰かの後ろに隠れていると勝てるか?
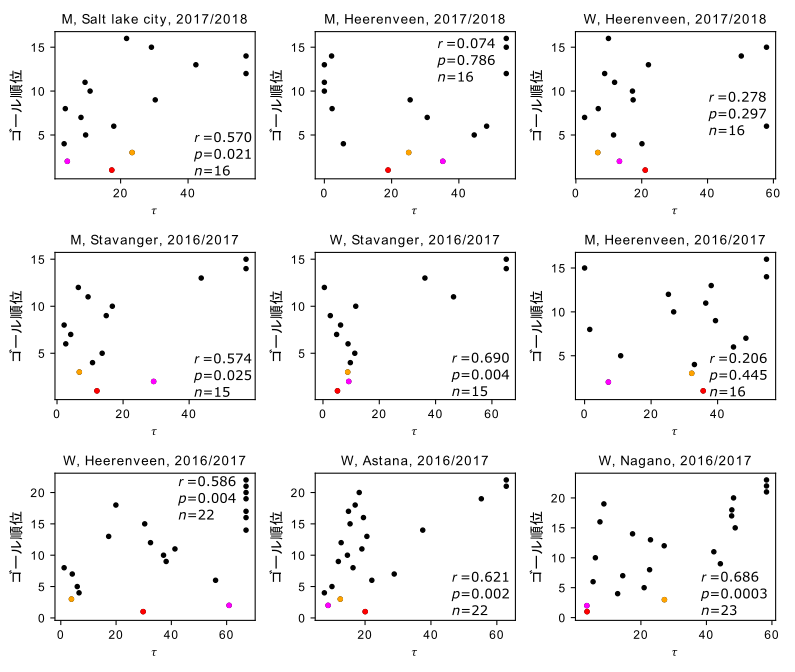
次に,メインの結果です.誰かの後ろに隠れている時間が長いと勝ちやすいでしょうか? 以下のグラフを見ましょう.
9個あるパネルの各々が,1つのレースを表しています.各パネルで,ひとつひとつの点が一人の選手を表します.横軸の$\tau$は,誰かの後ろに隠れていなかった(高い空気抵抗にさらされた)合計時間です.単位は秒です.誰かの後ろに隠れていることの定義は,頭全体が前の人の肩幅にすっぽり入っていて前の人から距離が一定以上離れていない状態とします.なので,そうなっていない時間の合計が$\tau$です.レース終盤(先頭が残り3周に入ってから残り1周に到達するまで)で$\tau$を計測しました.集団の先頭にいる選手や1人で滑っている選手の$\tau$は大きくなります.誰かの後ろにずっと隠れることができた選手は$\tau$が小さくなります.縦軸はゴール順位です.数値が小さいほど先にゴールしたということです.数値が1なら1位でゴールしたことになります.
$\tau$が小さい(空気抵抗にさらされている時間が短い)ほど順位が高ければ,誰かの後ろに隠れている時間が長いと勝ちやすいということになります.そうなっているでしょうか? 確かに,グラフが右肩上がりになっているように見えます.相関係数$r$の値も全てのレースで正なのでそういう傾向はありそうです.実際,9レース中6レースで,この傾向は統計的に有意でした.また1位でゴールした選手は赤,2位はピンク,3位はオレンジの点で示しています.これらの点は,グラフの左下(右下ではなく)に集まっていることが多いので,上位でゴールした選手は$\tau$が小さい傾向が見えます.したがって,マススタートでは誰かの後ろに隠れた時間が長いほど勝つ傾向にあることが分かります.
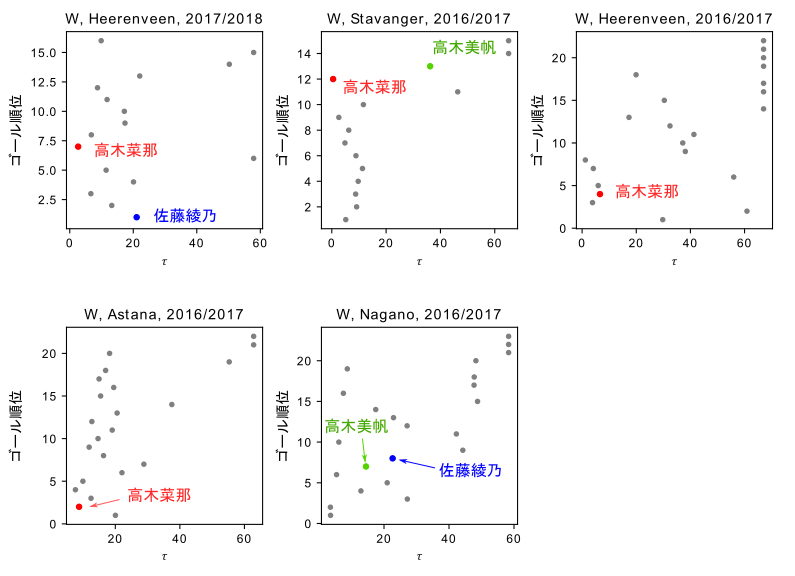
以下の図は,出版された論文 [1] では,はっきりと出しませんでしたが,日本人の女子選手の$\tau$とゴール順位の関係を見たものです.
髙木菜那選手が隠れるのが上手い($=\tau$の値が小さい)ことが分かります.
単にベストタイムがいいだけでは?
隠れるのが上手い選手は上位でゴールする傾向がある,と述べました.しかし,そうではなくて個人のスピードスケート競技でベストタイムが良い選手(地力がある選手)が単に勝っているのではないか? という反論が考えられます.そこで論文 [1] では,個人のスピードスケートのベストタイムが速い人がマススタートのレースでも勝ちやすいかどうかを調べました.その結果,そのような傾向はありませんでした.
議論
最後にこの話をゲーム理論にひもづけて議論しました.以下の図をご覧ください.
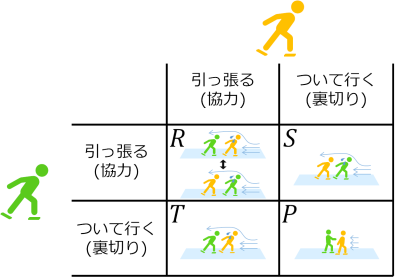
選手の戦略を大胆に単純化して,集団を引っ張って空気抵抗を受けるか誰かの後ろに隠れてついて行って空気抵抗を減らすという2つの選択肢だけを考えます.選手が2人だけであるというさらなる単純化をして,以下の3つの状況を区別します.
- 1人が引っ張ってもう1人がついて行く状況.ついて行く人が最終的に勝ちやすいと考えて,ついて行く人の利得(得点のこと)$T$は最大であるということにします.一方で,引っ張る人は空気抵抗を受けて勝つ確率が減るので,引っ張る人がもらう利得$S$は割と小さいと考えます.
- 2人ともついて行く状況.この状況では,2人とも,空気抵抗を受けないように先頭を譲り合います.すると,そうこうしているうちに,この2人の選手とは別の選手が先頭に立って逃げて勝つ可能性が高まり,そうなったら最悪です.したがって,この時の2人それぞれの利得$P$は最小と考えます.
- 2人が交替しながら引っ張る状況.お互いに,空気抵抗を受ける時間を,1人で滑っているときの半分に減らすことができます.したがって,この時の2人それぞれの利得$R$はそこそこ大きいですが,終始後ろに隠れている場合の利得$T$よりは小さいと考えます.
これらの状況をまとめると$T>R>S>P$となり,ゲーム理論でチキンゲームと呼ばれるゲームと同じ$T,; R,; S,; P$の関係になっています。このスケーターのジレンマは多人数のチキンゲームと考えることができるかもしれません.
おわりに
本記事を以下のようにまとめます.
- マススタートでは,ゴールに近づくに連れて,上位でゴールした選手は徐々に自分の位置を上げていきやすい.
- マススタートでは,誰かの後ろに隠れる時間が長いほうが勝つ傾向にある.
- マススタートでは,地力がある人が勝ちやすいわけではない.
- マススタートをゲーム理論的に分析できる可能性がある.
参考文献
[1] Ichinose G, Miyagawa D, Ito J, Masuda N (2020) Winning by hiding behind others: An analysis of speed skating data. PLoS ONE 15(8): e0237470.