こんにちは、えいりんぐーです

12月10日のダイナミックプライシングの勉強会にて、「ダイナミックプライシングの基本のキ」というタイトルで発表します。
割と応募が多く、来られない人もいるようなのと、理解の整理のために、ダイナミックプライシングの基本について、記事に書き起こします。
当日いらっしゃる方はよろしくお願いします。

~~ま〜私は前座なので気楽に~~

本記事の目的

~~同僚からダイナミックプライシングについて発表してほしいと言われた時に、~~上司やクライアントからダイナミックプライシング (以下DP) について基本的なアイディアを調べて欲しい、取り組む価値があるか検討して欲しい、と言われた時に、DP の基礎的な部分を説明できるようになることです。

ダイナミックプライシングでよくある前提

まず、よく DP が導入される状況について整理します。

需要の変動
供給の制限
- 在庫が有限
- 期間が有限
- c.f. 本、SaaS
技術的に容易
- 需要と供給の観測
- メニューコスト (価格変更コスト) の低さ
消費者の性質
- 価格変更への受容性
- Myopic (近視眼的、現在価格のみで判断する)

もちろん、業界によってあったりなかったりする条件があり、また現実には消費者は過激な価格変更には反発すると考えられます。

やる価値ある? ~またはROI~

では状況が当てはまるとして、DP の導入がコストに見合うか簡単に考察しましょう。
というのは、半分手前味噌ですが、某勉強会で、会計的な側面でデータ分析の価値を説明している方がいたので、それに倣い、DPに取り組む価値があるかどうかの一例を示します。

架空の会社Aが存在し、売上が500M円、利益率5%とすると、利益が25M円となります (Mは百万)。
DP による価格変更で売上が1%伸び、売上の伸びによる変動費などコストの増加はないとします。
この時、純粋に $500M {\times} 0.01 = 5M$ 円が利益に加算されます。
利益の上昇率は $5M \div 25M = 20$ % なので、極めて大きな収益上昇です。
利益率は $30M \div 505M \times 100 = 5.94$ % です。

この計算だと、(回収期間にもよりますが) 投資が5M円程度であれば、十分に取り組む価値があると言えます。
ちなみに大手航空会社ANAだと、売上2兆円なので、1%の増加で利益が大雑把に200億円も増加します。

価格の決まり方

それでは本題です。
経済学の理論的には価格は、需要と供給のバランスで決まります。
ただ、現実的には多くの場合で売り手側が価格を決めます。
この売り手側が価格を決める場合で、市場の状況に応じて価格を変化させることをダイナミックプライシングと言います (厳密な定義は割愛)。
逆に、買い手側が価格を決める場合もあり、オークションがそれに当たります。

需要と供給

下の図では、需要について価格と量の関係を示す需要曲線と、供給について価格と量の関係を示す供給曲線を表しています。
両曲線の交点で、最適な価格 $P^*$ が決まります。

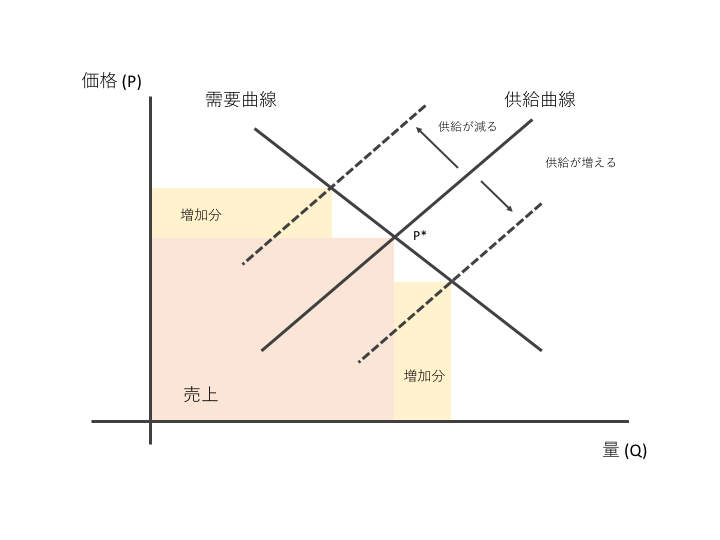
アパレルや食料品のように、新しいロットが入荷し、供給が増えると価格を下げることで、追加の利益を上げることができます。
逆に、航空券やホテルのように、空きが少なくなると価格を上昇させて、利益を増加させることができます。

売上の最大化

DP では、価格を変更することによる、売上最大化を企図します。
売上 $R$ は価格 $P$ と数量 $Q$ で表せます。

R = P \times Q

数量 $Q$ は、需要曲線で見たように、価格に応じて変化します。
ここで、とても単純な場合を考え、(数量を需要と同等とみなして) 需要の価格弾力性というものを導入します。
一般に A の B 弾力性と行った場合、B の変化量に対する A の変化量を指します。
需要の価格弾力性は次のように表せます。

-E = \frac{dQ / Q}{dP / P}

$E$ が1より大きい場合は、価格弾力性が高く、価格の変化で需要が著しく変わることを意味します。
上記の式を解くと以下のようになります。

Q(P) = CP^{-E}

ですので単純には、上式を使って$R = P \times Q(P)$ を最大化すればいいことになります。

需要の関数の具体例

実際には、需要 $Q$ は価格だけではなく、時間や在庫量およびそのほかの要素にも影響を受けます。

アパレルブランド Zara の DP を取り扱った Caro and Gallien 2012 では、需要の関数 $\lambda^w$ を商品の購入量 $C$、商品の古さ $A$, 前週の需要 $\lambda^{w-1}$、在庫 $I$、価格 $p$ の関数として求めています。

\lambda^w = f(C, A, \lambda^{w-1}, I, p)

一方で、航空券の DP を扱った Christ 2011 では需要を、曜日や期間で決まる潜在需要 $f(x)$ と、それらに加えて価格で決まる顧客の反応率 $g(x, p)$ とに分離して導出しています。

\lambda = f(x)g(x, p)

$g(x, p)$ には、Discrete Choice Model という顧客が離散的な選択肢の中から一つを選ぶ行動モデルの下、多項ロジスティックモデルが採用されています。

時間と在庫を考慮する

ここまでで、売上は価格と需要の積として求まり、需要の関数の例を紹介しました。
DP では往々にして、販売期間や在庫に制限があるので、それを考慮する必要があります。
教科書的には、時点 $t$ で在庫 $c$ の売上を、次のように求めることが多いです。

\begin{align}
R(t, c) = max(Q(P_t) \times F_t(P_t) \times[P_t + R(t-1, c-1)] \\
 + Q(P_t) \times (1 - F_t(P_t)) \times R(t-1, c) \\
 + (1 - D(P_t)) \times R(t-1, c))
\end{align}

ここで、$F_t(P_t)$ は時点 $t$ での購入確率です。
販売の開始から終了まで、様々な在庫・価格状況の時を考慮して、売上を最大にするように価格を求めることになります。
これを素直に動的計画法で求めるのは、次元の呪いによって計算が困難になることが多く、近似などの工夫をすることが多いです。

まとめ

以上が DP の基本的な考え方になり、これまでの話を簡単にまとめます。

ダイナミックプライシングとは需給に合わせて価格を変更すること
価格 $P$ は売上 $R = P \times Q(P)$ を最大化するように求める
Q(P)は、一つの関数としても、複合関数としても求めることができる
$max. R$ を素直に求めるのは、計算量から難しいことが多いのでなんらかの近似が必要

そのほかの参考資料

ダイナミックテクノロジー社ブログ
 AirBnB の事例
 ブレインパッドブログ ~~(また手前味噌で申し訳ない)~~