ABC-C第11弾

• バチャ第11弾！！
• 全員全完で草

ABC051 「Back and Forth」

考察と解法

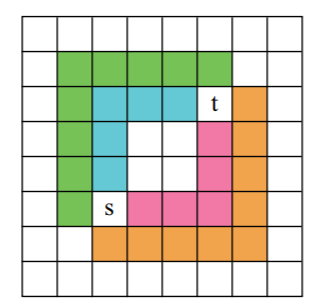
• この問題で一番大事なのは、絵を描くこと！！
• 絵を描くと、以下の画像のルートをたどることが分かる。
• 水色が内側を通った方がいいのでは？とか思うけど、絵をかけば内側通っても外側通っても変わらないことが分かる。

コード

#include <bits/stdc++.h>
using namespace std;

string ans = "";
int sy, sx, ty, tx;

int main() {
   cin >> sx >> sy >> tx >> ty;

   int dy = abs(sy - ty), dx = abs(sx - tx); // 制約の読み間違いとかが怖いので絶対値を取った
   ans += string(dy, 'U') + string(dx, 'R');                // Path1
   ans += string(dy, 'D') + string(dx, 'L');                // Path2
   ans += 'L' + string(dy+1, 'U') + string(dx+1, 'R') + 'D'; // Path3
   ans += 'R' + string(dy+1, 'D') + string(dx+1, 'L') + 'U'; // Path4

   cout << ans << endl;

   return 0;
}

感想

• 絵を描くって大事だね！！ってなる。これまじで。ほんとに。
• 絵をかいて気づきを得ることが多いので常に考察の候補にお絵かきを入れておきたい
• 上記の画像、AtCoderのeditorialからそのまま引っ張ってきたけど大丈夫かな？（権利的に）

ABC052 「Factors of Factorial」

考察

• $N!$の約数の個数を求めたい。
• $N!$を求めてからループで約数の個数を求めたい。しかし$1 \leq N \leq 10^3$なため、$N!$を求める過程でオーバーフローしてしまう。たとえ求めることができたとしても、$N!$は非常に大きな値となるためループで約数の個数を求めることは難しそう。つまり、なにかしらうまい方法を考える必要がある
• そこで、$N!$を分解して考えてみる。例えば$5!$を分解すると$5 \times 4 \times 3 \times 2 \times 1$となる。それぞれの数について素因数分解すると、$5 \times 2^2 \times 3 \times 2 \times 1$となる。整理すると、$5!=5 \times 3 \times 2^3 \times 1$となる。ここで、${5, 3, 2^3 }$をいろんな通りで組み合わせることで$5!$の約数の個数が求められそうだと気づく。$1$を掛け合わせても数値に変化はないため、$1$は除外した。
• もうちょっと考えてみる。$5$を$a$個、$3$を$b$個、$2$を$c$個を組み合わせることで約数の個数が求められそう。この$a, b, c$の値が分かればそれを掛け合わせるだけで答えを求めることができる。素数のみを組み合わせるため、組み合わせた結果の数値は一意に定まる。なので、どの素数が何個あるかだけに注目すればいい。
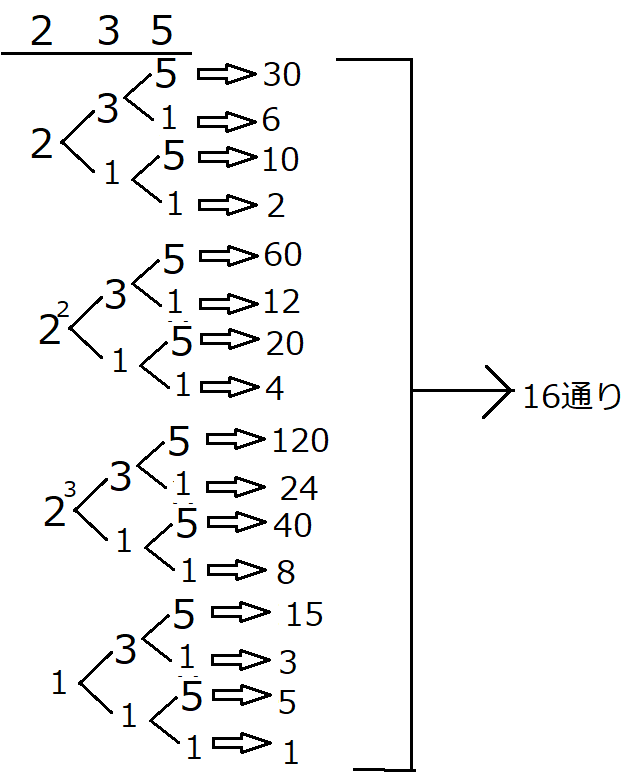
• $a$の値は、$5$を選ぶか選ばないかの2通りなので$a=2$となる。$b$の値も同様に、$3$を選ぶか選ばないかの2通りなので$b=2$となる。$c$の値は、$2, 2^2, 2^3, 2を選ばない$という4通りがあるので$c=4$となる。これらの値を掛け合わせると、$abc=2\times 2 \times 4 = 16$となる。実際に組み合わせを図として書くと以下のようになる。（数を選ばないときは、1を掛けることにするが、他の数値に影響はない）

• ここで、$(素数xの個数+1)(素数yの個数+1)(素数zの個数+1)...$といったようにすれば約数の個数が求められることに気が付く。$+1$はその素数を選ぶか選ばないかを示している。
• つまり、1からNまでの素数の個数を求めて、$(素数xの個数+1)(素数yの個数+1)(素数zの個数+1)$のように掛け合わせれば答えを求めることができる。

解法

• $N!$を$N, N-1, N-2, ...$のそれぞれについて分けて考える。
• $N-i$を素因数分解して、各素数がいくつあるのかを求める
• 最後に、$(a+1)(b+1)(c+1)...$をしていけば答えを求めることができる。（$a, b, c,...$は素数の個数）

コード

#include <bits/stdc++.h>
using namespace std;

using ll = long long;

const ll MOD = 1e9 + 7;
int N;
map<int, int> mp; // map[x]: 素数xが何個あるか？

int main() {
   cin >> N;

   for (int i = 2; i <= N; i++) { // N,N-1,N-2,..について各素数の個数を求める
      int x = i; // iを変更するとまずいのでxに値をコピー
      for (int j = 2; j <= x; j++) { // 素数jの個数を求める
         while (x % j == 0) {
            x /= j;
            mp[j]++;
         }
      }
   }

   ll ans = 1;
   for (auto x : mp) {
      ans = ((ans%MOD) * (x.second+1)%MOD) % MOD;
   }

   cout << ans << endl;

   return 0;
}

• 上位陣はみんな大体同じコードだったけど、なにやってんのか理解できない...なんか上手い方法があるんだろうなーと思ってる。

感想

• $N!$のままでは考えにくいから、それを分解するという考え方が大事だったように思う
• 要素を分解するぜ！！みたいな考え方はよく使う気がする。けど問題といてるときに思いつくとは限らない...
• 以前解説を読んでも分らなかった問題が解けたので、なんで解けたんだろーって感じ。

ABC053 「X: Yet Another Die Game」

考察

• サイコロを90度回転させるとどういった遷移をするのかを考える。
• 制約により、自分のマス＋遷移先のマスが7にならないような4通りのマスに遷移できる。例えば、今が1のマスにいるなら6以外の4通りのマス{2, 3, 4, 5}に移動できる。
• $x$が小さいなら愚直にできそうだけど、$x_{max}=10^{15}$なため、なにかしら上手い方法を考える必要がある。
• ここで、$10^{10}$みたいなめちゃくちゃでかい数が入力されたらどうするかを考える。直感的に思い浮かぶのは、ある程度まで「6→5→6→5→...」の遷移をさせる方法。常に最大値を取るので操作回数も少なくなる。
• 「6→5」と遷移すると11点が加算される。この操作が何回あるかを求めたいので、$2 \times \frac{x}{11}$で求める。
• 11点単位で加算する操作の後に残る数は$0 \leq num \leq 10$である。$num$が0ならもう操作する必要は無い。$num$が7以上なら後2回の操作で$x$以上になる。$num$が6以下なら後1回の操作で$x$以上になる。

解法まとめ

• $2\times \frac{x}{11}$によって「6→5」の遷移を何回するかを求める。この回数を$cnt$とする
• $x$を11で割った余り$a$の数値によって場合分けする
  • $a =0$なら、もう操作をする必要は無いので答えは$cnt$となる。
  • $1 \leq a \leq 6$なら、あと1回の操作で条件を満たすため答えは$cnt+1$となる。
  • $a \geq 7$なら、あと2回の操作で条件を満たすため答えは$cnt+2$となる。

コード

#include <bits/stdc++.h>
using namespace std;

using ll = long long;

int main() {
   ll x;
   cin >> x;
   ll cnt = (x / 11) * 2;
   x %= 11;

   if (x == 0) {
      cout << cnt << endl;
   } else if (x <= 6) {
      cout << cnt + 1 << endl;
   } else {
      cout << cnt + 2 << endl;
   }

   return 0;
}

感想

• ちゃんと考察してからコーディングできたので良い感じ。

ABC054 「One-stroke Path」

考察と解法

• DFSで解けそうだな。
• 訪れたかどうかを管理する配列を用意してやる必要がありそう。
• 同じ頂点には訪れずに$N-1$回の遷移に成功したときにカウントする。

コード

#include <bits/stdc++.h>
using namespace std;

int N, M;
vector<int> G[100];
bool visited[100];

int dfs(int from, int cnt) {
   if (cnt >= N-1) {
      return 1;
   }

   visited[from] = true;
   int ret = 0;
   for (int to : G[from]) {
      if (visited[to]) continue;
      ret += dfs(to, cnt+1);
   }
   visited[from] = false;

   return ret;
}

int main() {
   cin >> N >> M;
   for (int i = 0; i < M; i++) {
      int a, b;
      cin >> a >> b;
      a--, b--;
      G[a].push_back(b);
      G[b].push_back(a);
   }

   cout << dfs(0, 0) << endl;

   return 0;
}

感想

• なんとなくDFS実装できてしまったんだが、何か説明できない得体の知れない力によって書いた感がある。結構難しい実装だった気がするけど、なんで書けたのかよく分らん
• next_permutationでも解けたみたい。暇だったら実装してみよーかな

ABC055 「Scc Puzzle」

考察と解法

• できるだけたくさんの文字を作りたいので、文字の浪費は避けたい。
• cのみでSccを作ると4文字使ってしまう。だが、Sとcの組み合わせなら3文字でSccをつくることができる。なので、Sとcの組み合わせを優先的に考える。
• Sとcの組み合わせで作れるSccの個数は$a = min(N, \frac{M}{2})$となる。
• 残りのcの個数は$M-2a$個である。よって、cのみで作れるSccの個数は$b=\frac{M-2a}{4}$となる。
• 答えは$a+b$となる。

コード

#include <bits/stdc++.h>
using namespace std;

using ll = long long;

int main() {
   ll N, M;
   cin >> N >> M;
   ll a = min(N, M / 2); // Sとcの組み合わせで作る
   ll b = (M - 2 * a) / 4; // cのみで作る
   cout << a + b << endl;

   return 0;
}

感想

• できるだけたくさんの文字を作るには、文字の浪費を避けたい。ではどうすれば避けられる？といった考え方が重要だったと思う。