問題を解く前に
動的計画法とは
動的計画法とは
- いくつかの小さな問題の解や計算結果を利用してより大きな問題を解く。
- 同じ計算をすることを防ぐため、表に計算結果を記録し利用する。
というような条件を満たすアルゴリズムである。
問題
- コイン問題
- 額面がc1, c2,..., cm 円の m 種類のコインを使って、 n 円を支払うときの、コインの最小の枚数を求めて下さい。各額面のコインは何度でも使用することができます。
- 入力
M N
c1 c2 ... cn - 出力
コインの最小枚数を1行に出力してください。 - 制約
- 1 ≤ n ≤ 50,000
- 1 ≤ m ≤ 20
- 1 ≤ 額面 ≤ 10,000
額面はすべて異なり、必ず1を含む
なぜ動的計画法をつかうのか
なぜ動的計画法を使うのか、それは計算が入れ子構造になっているからである。例えば、使えるコインの枚数が2枚で5円を支払う時、2枚目のコインが2円だったとする。(1枚目は1円)
2枚目のコインを1以上枚使うと考えると、5-2=3円となりN=3のときの問題に帰着する。つまりN=5の時の問題はN=3の時の問題を利用できる。また、N=3の時の問題もN=1の時の問題を利用していると考えられる。これは入れ子構造になっているといえる。つまり、この問題は動的計画法が有効であると考えられる。
考え方
実際にmを行としてnを列とした表を書いてその時のコインの最小枚数を埋めていく。
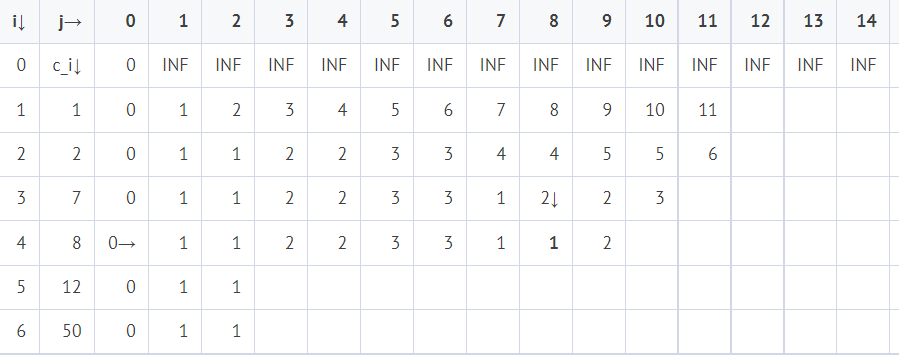
引用:https://o-treetree.hatenablog.com/entry/DPL1A
そこである規則に気づき以下のような漸化式が立つ。
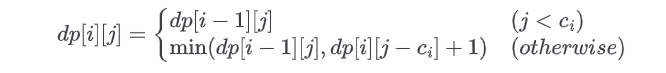
引用:https://o-treetree.hatenablog.com/entry/DPL1A
i:コインの番号
j:払う値段
ci:i番目コインの値段
を表す。
- 払う値段がi番目のコインより小さい場合(j<ci)の時
表の1つ上の枚数と等しくなる。これは表を見れば分かるが、i=3,j=4,ci=7のときがそうである。 - 払う値段がi番目のコイン以上の場合
dp[i][j-ci]+1はj(払う値段)からci(i番目のコインの値段)を引いた値である。これは「なぜ動的計画法をつかうのか」で説明したことを式に表している。ciのコインを使うと仮定してそのコインの値段分を引いたところの枚数をみている。そこにciのコイン分の+1をすればよい。その枚数と今までの最小枚数を比べることで最小枚数を決定する。
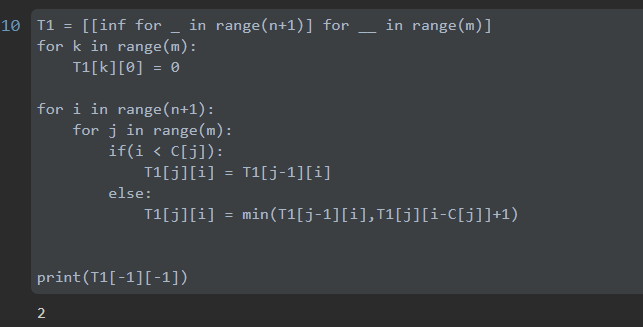
実装
プログラム
pytnonで実装した。
#%%
n = int(input("n>>"))
m = int(input("m>>"))
C = []
inf = 100000
T1 = [[inf for _ in range(n+1)] for __ in range(m)]
for k in range(m):
T1[k][0] = 0
for i in range(n+1):
for j in range(m):
if(i < C[j]):
T1[j][i] = T1[j-1][i]
else:
T1[j][i] = min(T1[j-1][i],T1[j][i-C[j]]+1)
print(T1[-1][-1])
先ほどの説明と違ってiとjが逆になっていることに注意
- infで2次元配列T1を初期化している。
- for文で0円支払うときを表す0列目を0にする。
- 2重ループで漸化式を作る。
- 最後に配列の末尾を出力
出力結果
入力は
15 6
1 2 7 8 12 50
とした。その出力が2となった。これは7と8の組み合わせであり最小枚数であるから正しいと言える。