Courseraで受講したAudio Signal Processing for Music Applicationsの内容のまとめです。単純にトラックを再生するだけではなく、一歩踏み込んだものを作りたい、というときの入り口になる・・・と思います。
音声解析の目的
音声解析とは、ざっくりいえば「聞こえてくる音声がどんな周波数の音で構成されているか」を明らかにすることです。これをスペクトル解析といいます。
これを明らかにすると、以下のようなことができるようになります。
- 音の構成から、特徴づけを行う(楽器・発話者の特定、音楽のジャンルの推定など)
- 目的の周波数以外の音を除外する(フィルタリング)
- 音の合成によって目的のサウンドを構成する(シンセサイザーなど)
上記の点にもある通り、分解(解析)が上手くできれば、その逆の合成によって音を作り出すこともできるようになります。つまり、音楽解析は全体として分解->解析->(変換・フィルタリング)->再構築というプロセスになります(鋼の錬金術師的ともいえる)。
音声の表現
音声解析の第一歩は、音声を関数として表現するところから始まります。
$$
x[n] = Acos(\omega nT + \phi) = Acos(2\pi fnT + \phi)
$$
- $A$: amplitude 振幅->音の大きさ
- $\omega$: angular frequency in radius 角速度->音の高さ(周波数)
- $f$: frequency in Hz ($\frac{w}{2\pi}$)
- $\phi$: initial phase in radius 初期位相
- $n$: time index
- $f_s$: sampling rate サンプリング周波数
- $T$: sampling period in second (1/$f_s$, $t=nT=n/f_s$)
三角関数のグラフが音波に似ているのは記憶にあるのではないかと思います。これを利用し音を関数として表現します。
$\omega$の角速度は、その名の通りこれは単位時間(1秒)当たりに進む角度になっています。角度の単位はラジアンで(ラジアンって・・・という方はこちらをご参照)、ラジアンの場合$2\pi$で一周、つまり一周期なので単位がラジアンである$\omega$を$2\pi$で割ることで一秒間当たりの周回数$f$、つまりHzになります。
注意すべき点は、最終的に得られる音($x[n]$)のインデックスである$n$です。
この$n$は1進むと$T$秒進みます。$T$はサンプリング周波数の逆数で、サンプルの取得間隔になります。
サンプリング周波数は音を取得する頻度を表していて、これが高いほどより高い音(周波数が高い音)にも対応できます。サンプリング周波数は合成を行う時のために取得したい周波数の2倍以上の余裕を持っておく必要があり(サンプリング定理)、一般的なCDなどは、人間の可聴域が20,000Hz程度であるのに合わせその約2倍である44,100Hzが採用されています。
※ハイレゾと呼ばれる音源はこのサンプリング周波数が48,000Hzと一般的なCDのレートより高く、これがHigh Resolution=高解像度と呼ばれる所以です。聞こえないなら意味がないのではと思ってしまいますが、耳ではなく体で感じる空気感などがそのあたりに含まれているらしいです。
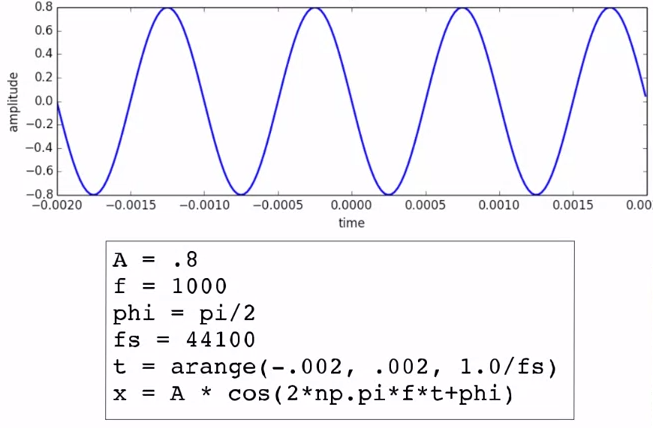
前置きが長くなりましたが、この関数に実際パラメーターを入れてプロットしたものが下図になります。音として聞くと、ポー、っという聴力検査の時のような音がします。
CC by MTG (Basic mathematics - Sinewave plot)
ただ、このままだと扱いずらいので、オイラーの公式を利用し指数関数での表現へと変換します。
$$
\bar{x}[n] = Ae^{j(\omega nT + \phi)} = Acos(\omega nT + \phi) + Asin(\omega nT + \phi)
$$
オイラーの公式は$e^{j\phi} = cos\phi + jsin\phi$という複素指数と三角関数の間の関係を示したもので(下図参照)、これを適用することで三角関数の表現を複素指数の表現に変換することが可能になります。
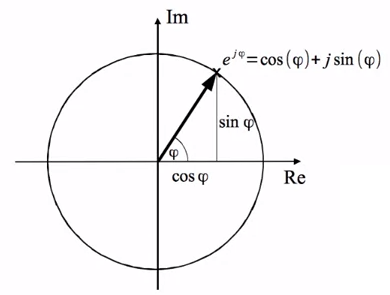
CC by MTG (Basic mathematics - Euler's formula)
複素指数表現にしたメリットとして、振幅である$A$は複素数の絶対値、初期位相である$\phi$は偏角として簡単に表せるようになります。

CC by MTG (Basic mathematics - Complex numbers)
これまでの話をまとめると、以下のようになります。
- 音は時間に関連した周期的な関数と仮定して、三角関数でこれを表現する
- 振幅$A$が大きいほど大きな音、角速度$\omega$が高いほど高い音になる
- 扱いやすくするため、三角関数表現はオイラーの公式を利用し複素指数の表現に変換する
- 複素指数表現の導入により、振幅は絶対値、初期位相は偏角で表現できるようになる
- 音はサンプリング周波数によって決定される単位時間ごとの値として表現される(離散時間表現)。具体的には、$x[n]$と$x[n+1]$の間の時間間隔は、サンプリング周波数を$f_s$とした場合$1/f_s$となる。
これで音が表現できるようになったので、次からはこの音声をいかに分解・再構築するかについて述べます。
音声の分解・再構築
分解(DFT:Discrete Fourier Transform)
結論からになりますが、音声の分解を行うのがフーリエ変換、再構築を行うのが逆フーリエ変換になります。ただ、コンピューターで扱う時間は上記で説明した通り離散的であるため、離散フーリエ変換・逆変換と呼ばれます。
まず、分解を行う離散フーリエ変換(Discrete Fourier Transform = 以下、DFT)がどのように定義されるのかを見てみます。
$$
X[k] = \sum^{N-1}_{n=0} x[n] e^{-j2\pi kn/N}
$$
- $N$: 標本数
- $n$: discrete time index
- $k$: discrete frequency index k=0,...,N-1
- $\omega_k = 2\pi k / N$: 角周波数
- $f_k = f_s k / N$: 周波数(Hz)
フーリエ変換の本質は、取得した$N$個の標本$x[n]$に、各周波数$k$の音がどれくらい含まれているかの内訳$X[k]$を調べることです。ただ、ここで$k$は単純な周波数ではないことに注意が必要です。
調べられる周波数の上限はサンプリング周波数$f_s$で決まりますが、ここから標本を$N$だけ取る場合は調べられるのは$f_s/N$ごとになります(=離散的)。この$f_s/N$がkの単位であり、よって$k$と周波数の関係は上記にある通り$f_k = f_s k / N$となります。要は調べられる周波数の細かさは標本数に依存するということです。
- $n$は離散時間の単位であり、$1/f_s$秒単位
- $k$は離散周波数の単位であり、$f_s/N$Hz単位(これをbinという)
この2点を押さえておかないと、以後単位変換で混乱することになります。
DFTにおける$e^{-j2\pi kn/N}$のパートは$x[n]$から目的の周波数$k$以外のものをキャンセルする効果があり(The Discrete Fourier Transform 2 of 2, Euler's identity Generalizations 参照)、$x[n]$にこれを掛け合わせることで$k$の分のみを取り出すことができます。
これを各時間$n$について計算しその和を取ることで、各時間$n$に含まれる$k$成分の和、つまり音全体の中に周波数$k$がどれくらい含まれるかを計算することができるようになっています。
実際に計算しプロットしたものが下図になります。
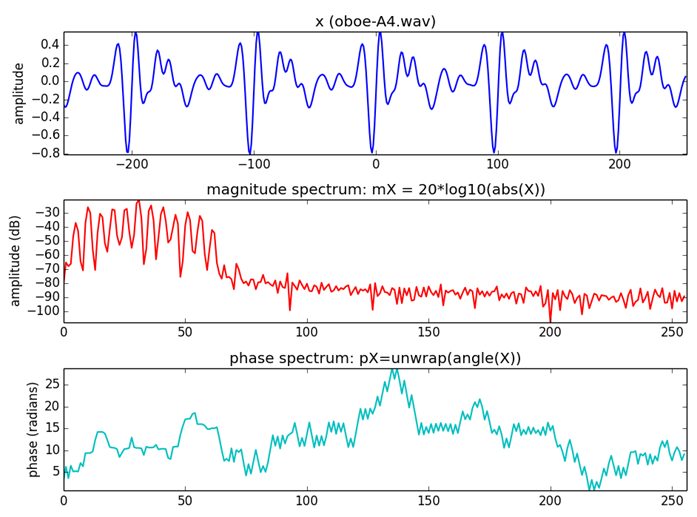
CC by MTG (The Discrete Fourier Transform 1 of 2)
1段目が実際の音、2・3段目がDFTの結果を示していて、2段目は振幅、3段目は初期位相のグラフになっています。
2段目は縦軸が振幅の強さをデジベルに変換したもの、横軸がHzとなっており、どの高さの音がどれくらい強くなっているかを示しています(これをmagnitude spectrumといいます)。
3段目は縦軸が初期位相(角速度)、横軸がHzとなっており、どの高さの音がどのタイミングで鳴り始めるかを示しています(これをphase spectrumといいます)。
ここで、関連する事項を少しまとめておきます。
- Symmetry(対称性)
実際の音を分析すると、magnitude/phaseは左右対称になります。これは$A_ocos(2\pi k_0 n/N) = \frac{A_0}{2}e^{j2\pi k_0 n/M} + \frac{A_0}{2}e^{-j2\pi k_0 n/M}$の式を展開していくと導くことができ、この場合$k=k_0,-k_0$の2点、つまり原点を中心とした線対称の形でmagnitudeが出現します。
(厳密には実部のみで構成される音(普通の音)の場合magnitudeは偶対象・phaseは奇対称、実部と虚部で構成される場合magnitudeは偶対象でphaseは0となる)

CC by MTG (The Discrete Fourier Transform 2 of 2 DFT of real sinusoid)
マイナス側はいらないので、通常は0以上のパート(positive half)のみを扱います。
- Energy
magnitudeの二乗和をEnergyと呼びます。
$$
\sum_{n=-N/2}^{N/2-1}|x[n]|^2 = \frac{1}{N}\sum_{k=-N/2}^{N/2-1}|X[k]|^2
$$
- Desibel(デジベル)
magnitudeを表す単位で、以下で定義されます。
$$
db = 20 * log_{10}(abs(X)=magnitude)
$$
- Phase unwrapping
phaseは$2\pi$、つまり一回転すると0に戻るので、これを加味してphaseを加工することをunwrappingと言います。この処理を行うことで、phaseの推移が見やすくなります。

CC by MTG (Fourier Transform property 2 of 2 Phase unwrapping)
- Zero-padding
解析対象の音声の後ろに音声0の要素を加えることで、DFTで得られるmagnitudeのカーブが滑らかになりピークが推定しやすくなります。そのため、DFTを行うサイズである標本数$N$は実際の音のサイズ$M$に比べ大きくし、差を0で埋めて計算することが多いです。
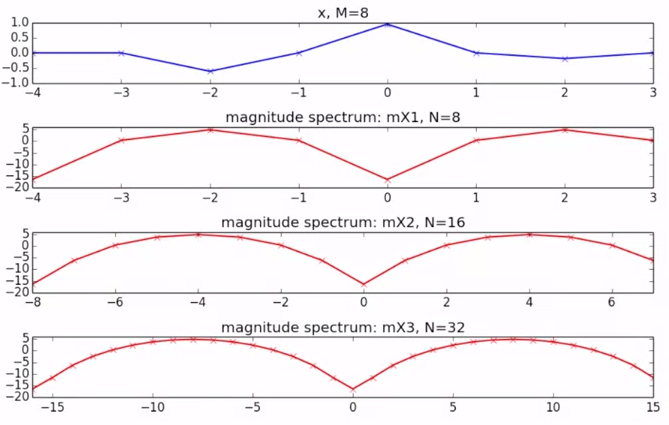
CC by MTG (Fourier Transform property 2 of 2 Zero-padding)
DFTを行い、magnitudeとphaseを明らかにすることが「音の分解」に相当するプロセスになります。
再構築(IDFT:Inverse Discrete Fourier Transform)
DFTを行った結果得られたmagnitudeとphaseを利用し、元の音を再構築するために使用されるのが、逆離散フーリエ変換(Inverse Discrete Fourier Transform、以下IDFT)になります。
$$
x[n] = \frac{1}{N}\sum^{N-1}_{k=0}X[k]e^{j2\pi kn/N}
$$
これはDFTとは逆の操作を行い音声を再合成しています。
高速化
実際計算する際は、DFT/IDFTを高速化した高速フーリエ変換/逆変換(FFT/IFFT)を利用します。
FFTを利用する際は、以下の操作を行います。
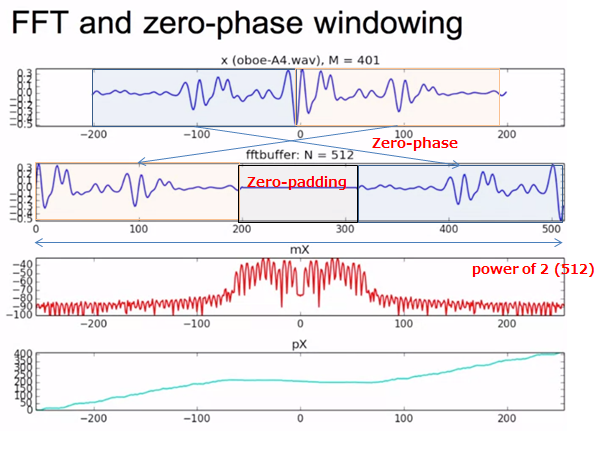
- Zero-phase windowing (言葉で説明しずらいので、下図参照)
- サイズを2の累乗に合わせる(128, 256, 512・・・)
- 合わないサイズの分を0で埋める(Zero-padding)
FFT/IFFTはscipyに実装されており、それを利用し簡単に実装することができます。
上記の説明はコードで見た方が早い面もあるので、こちらもご参考ください。
MTG/sms-tools/software/models/dftModel.py
これで音声の分解、そして再構築ができるようになったと思います。
ただ、このままでは単純に元の音を再構築しているだけなので、ここから分解結果の解析方法についてもう少し踏み込み、その後はいよいよ変換やフィルタリングに関わる箇所を見ていきたいと思います。
音声分解結果の解析
時系列変化の解析(STFT:Short-Time Fourier Transform)
一般的な曲は数分間の長さがあり、これをFFTにかけた場合曲の中のいろいろなタイミングで鳴っている音が混じり合い、magnitudeもphaseも雑然として特徴がつかみずらいものになってしまいます。
そこで曲を一定の長さで分割していき、分割単位ごとに離散フーリエ変換を行います。これを並べていくことでmagnitude/phaseの時系列での変化が把握できます。この手法を短時間フーリエ変換(Short-Time Fourier Transform = 以下、STFT)と呼びます。
$$
X_l[k] = \sum^{N/2-1}_{n=-N/2}w[n]x[n+lH]e^{-j2\pi kn/N}
$$
- w: analysis window
- l: frame number (0,1,...)
- H: hop size
サイズNの分析範囲をHずつずらしていくイメージです(下図参照)。
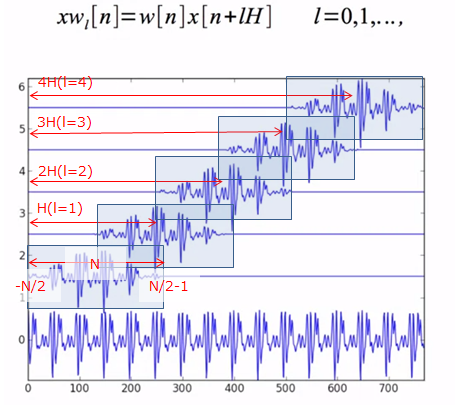
CC by MTG (The Short-Time Fourier Transform (1 of 2))
$w$はwindow function(窓関数)と呼ばれるものです。なぜこんなものをかけているのかというと、切り出したサイズNの部分は「周期的な信号」であるとの仮定をしているためです。ただ、実際は当然そうではないため、最初の方は0で最後に0へ収束するような関数をかけて周期的な信号であるかのように見せかけます。このための関数がwindow function(窓関数)と呼ばれるものです。
こんなものをかけてしまって大丈夫なのかという気がするかもしれませんが、逆に窓関数をかけない場合「周期的な信号」という仮定が崩れてしまうため、音声を再構築した際ノイズを含んだような音になってしまいます。
窓関数は具体的には以下のような関数です(以下は単純な矩形窓(rectangular window))。
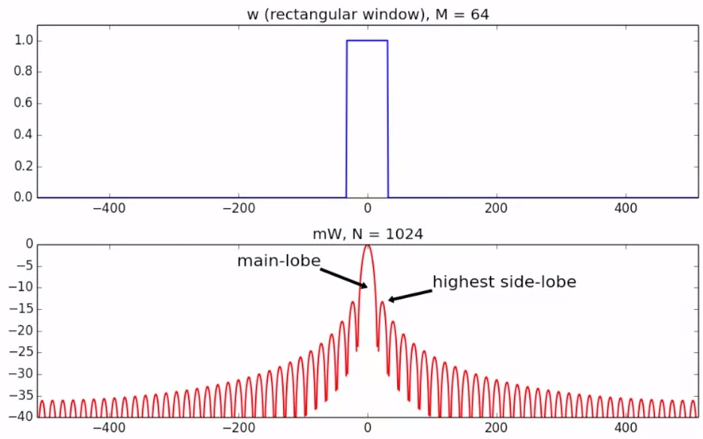
CC by MTG (The Short-Time Fourier Transform (1 of 2) Analysis window)
ピークである箇所で1の値を取り、その周辺で減衰する単峰型の形をとります。
そのmagnitudeを取ると上図のようになり、ピークの所をmain-lobe、ピークの隣の峰をside-lobeと呼びます。
窓関数は目的の周波数のみ通すのが好ましいので、main-lobeが狭い方が周波数の分解能が高く、main-lobe以外のside-lobeがなるべく低い方がメイン以外の音(小さな音)への影響が少なくなります。main-lobeの狭さとside-lobeの低さはトレードオフの関係にあり、状況に応じ使い分ける必要があります。
一般的には、大きい/小さい音が双方含まれるケースではside-lobeが低いものを選び、一定の大きさに収まっているような場合は分解能を優先しmain-lobeが狭いものを選択します(前者はblackman/blackman-harris、後者はhamming/hanningが使われることが多いです)。
<参考>
Window function Windowing
Understanding FFT Windows Choosing a Windowing Function
Sinusoidal model
複雑な音を、特定周波数のシンプルな音(Sinusoid)の集合という風に考えるのが、Sinusoidal modelになります。
以下のモデルでは、時刻nにおける音をR個の特定周波数の音で表現しています。
$$
y[n] = \sum^R_{r=1} A_r[n]cos(2\pi f_r [n]n)
$$
- $R$: サイン波の数
- $A_r[n]$: 時刻nにおける振幅
- $f_r[n]$: 時刻nにおける周波数
このモデルに当てはめることができれば、シンプルな音から複雑な音を再構成することも出来そうです。
では、ある音がどんな周波数の音で構成されているかはどう調べればよいでしょうか。この手がかりになるのは、やはりスペクトルになります。
スペクトル分析を行うと、以下のように異なる周波数の音がmagnitudeのピークとして検出されるのがわかります。
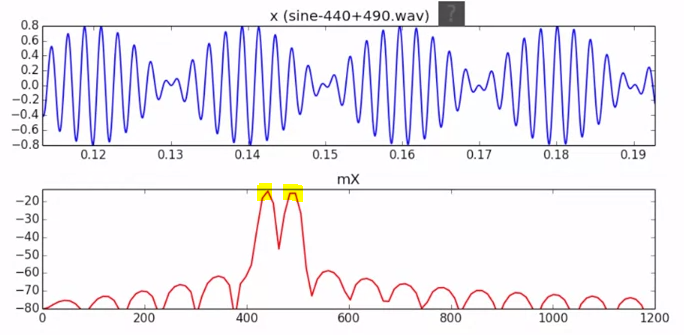
Week 5: Sinusoidal model, Theory lecture 1: Sinusoidal model 1
よって、以下の手順を踏むことで音を構成する周波数がうまく特定できそうです。
- ピークがうまく検出できるよう、magnitude spectrumを作成
- ピークの位置を特定
まず、「1. ピークがうまく検出できるよう、magnitude spectrumを作成」から行きます。このポイントとなるのがwindow sizeで、複数の周波数成分がそれぞれwindowの中に収まるように設定を行う必要があります。
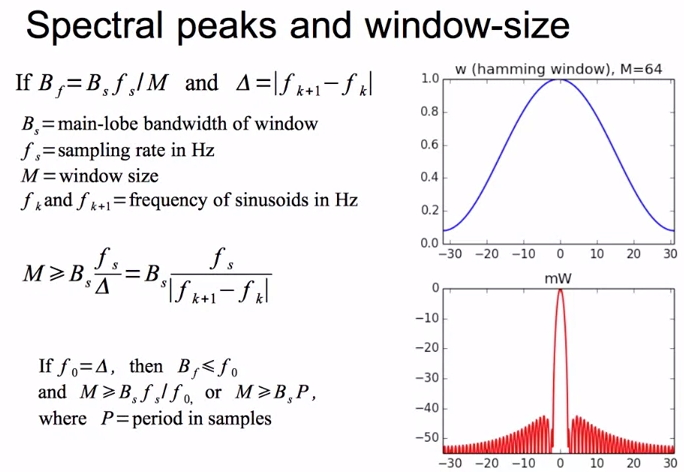
Week 5: Sinusoidal model, Theory lecture 1: Sinusoidal model 1
上記の通り、検知可能な周波数は$f_s/N$単位になるため、これが検知しようとしている2つの周波数の差異よりは小さい必要があります(そうでなければ2つの周波数を分解できないため)。
これより、まず$\frac{f_s}{|f_{k+1} - f_k|}$が導出されます。
そして、窓関数のmain lobeの中に納まるbinの数はそれぞれ決まっており、これが$B_s$になります。よって、$B_s \frac{f_s}{|f_{k+1} - f_k|}$で適切なサイズが導出できる、というわけです。
上記の440/490が混ざった例だと、以下のようになります。

Week 5: Sinusoidal model, Theory lecture 1: Sinusoidal model 1
まあ、実際はその音の周波数がどうなっているかは知る由がないので(440と490だ!とか)、100~2000Hzくらい、とあたりを付けてその間の周波数全体でうまく働くようなMを決めます(こんな感じ。横軸が周波数で、縦軸がk(M=k * 100 + 1とする)。k=21ぐらいでどの周波数でも安定するので、2101をMとして使用する)。
- ピークの検知方法
- Sinusoidモデルによる分解・合成
Harmonic model
Sinusoidal plus residual model(Stochastic model)
変換・フィルタリング
フィルタリング
A3: Fourier Properties Part-4: Suppressing frequency components using
DFT model より引用
変換
Week8 - Sound transformations
音声の分類
Week9 - Sound and music description
音声解析研究の世界へ
Week10 - Concluding topics