ベイズの識別規則の概要
3章では、ベイズの定理を用いた識別方法について述べられている。
ベイズの定理とは、観測データを$x$、その識別クラスを$C_{i}(i=1, ... K)$とする時、$x$があるクラス$C_{i}$に所属する確率$P(C_{i}|x)$を以下のように表せる、という定理である。
P(C_{i}|x) = \frac{p(x|C_{i})}{p(x)} \times P(C_{i})
これは観測データ$x$が発生しかつそれが$C_{i}$に所属する確率(同時確率)$p(C_{i},x)$について以下の等式が成り立つことから導ける。忘れそうになったら、ここから逆算すると良い。
p(C_{i},x) = p(x|C_{i})P(C_{i}) = P(C_{i}|x)p(x)
ここで、今後登場する用語を整理しておく。
| 式 | 概要 |
|---|---|
| 事前確率 | $C_{i}$のデータが発生する確率。$P(C_{i})$ |
| 事後確率 | $x$が観測された時$C_{i}$に分類される確率で、求めたい対象。$P(C_{i}|x)$ |
| 尤度 | $C_{i}$の中で$x$が発生する確率($x$が$C_{i}$であることが尤もらしい度合い)。$p(x|C_{i})$ |
| 周辺確率 | 観測データ$x$が発生する確率。$p(x)$ |
実際のデータを例に、どの用語がどういった定義となるのかを見ていく。下記に、仮の健康データを用意した。
| アンケート対象 | 喫煙する($S=1$) | 飲酒する($T=1$) | |
|---|---|---|---|
| 健康($G=1$) | 800人 | 320人 | 640人 |
| 健康でない($G=0$) | 200人 | 160人 | 40人 |
| 計 | 1000人 | 480人 | 680人 |
ここで、喫煙して飲酒する($S=1, T=1$)人を健康と判定していい確率はどれくらいかを知りたいとする。これをベイズの定理に当てはめると以下のようになる。
p(G=1 | S=1,T=1) = \frac{p(S=1,T=1|G=1)}{p(S=1,T=1)} \times P(G=1)
$P(G=1)$、健康であるひとの事前確率は、アンケート対象の総数1000人のうち800人なので、$\frac{800}{1000} = \frac{4}{5}$。
$p(S=1,T=1|G=1)$、健康である人の中で、喫煙・飲酒両方する人の確率(尤度)は、$\frac{320}{800} \times \frac{640}{800} = \frac{2}{5} \times \frac{4}{5} = \frac{8}{25}$となる。
$p(S=1,T=1)$、喫煙もして飲酒する人の割合は、健康な人の中での割合と、健康でない人の中での割合を足し合わせたものになる(つまり、各クラスにおける該当ケースの発生確率を足し合わせることになり、この操作を周辺化という。そのため周辺確率という名前がついている)。
健康であり、喫煙もして飲酒もするケースの確率は、まず健康である確率($P(G=1) = \frac{4}{5}$)に、健康である人の中で、喫煙・飲酒両方する人の確率$p(S=1,T=1|G=1) = \frac{8}{25}$を掛け合わせたもの、つまり$\frac{4}{5} \times \frac{8}{25} = \frac{32}{125}$となる。
これと同様の計算を健康でない人についても行うと、
P(S=1,T=1,G=0) = P(S=1,T=1|G=0) \times P(G=0) \\
= (\frac{160}{200} \times \frac{40}{200}) \times \frac{200}{1000}
= (\frac{4}{5} \times \frac{1}{5}) \times \frac{1}{5} = \frac{4}{125}
よって、$p(S=1,T=1) = \frac{32}{125} + \frac{4}{125} = \frac{36}{125}$となる。
これで必要な値は全て求まったので、「喫煙して飲酒する($S=1, T=1$)人を健康と判定していい確率」、つまり事後確率は、
p(G=1 | S=1,T=1) = \frac{8}{25} / \frac{36}{125} \times \frac{4}{5} = \frac{8}{9}
となる。この場合だと、喫煙して飲酒する人は健康と判断していいことになる(確率的に)。この判断を尤度の比で行うこともできる(3.1.3参照)。
実際に識別を行う場合は、どのクラスの場合に事後確率が最大となるかで判断することになる。この判断方法であれば誤り率を最小化できることが証明できる(3.1.4参照)。
モデルの改良
損失の考慮
先程の例でいえば、本当は病気である人を健康と判断してしまった、つまり病気を見逃してしまった場合の損失は、健康である人を病気として判断してしまうケースより重く見た方が良い・・・と考えられる。
つまり単に確率のみでなくその判断による損失の大きさを考慮したほうが適切な判断ができる場合がある。具体的に言えば、損失の期待値を基に判断を行いたいということだ。
損失$L$を以下のように表してみる。
L =
\left(
\begin{array}{cc}
L_{健康 | 健康} & L_{健康 | 病気} \\
L_{病気 | 健康} & L_{病気 | 病気}
\end{array}
\right)
=
\left(
\begin{array}{cc}
0 & 20 \\
1 & 0
\end{array}
\right)
期待値は値と確率を掛け合わせたものの和になるため、損失の期待値を$r$とすると以下のように表現できる。
r(健康|x) = L_{健康 | 健康} P(健康|x) + L_{健康 | 病気} P(病気|x) \\
r(病気|x) = L_{病気 | 健康} P(健康|x) + L_{病気 | 病気} P(病気|x)
これに先程の喫煙・飲酒共にするケースの場合、$P(健康|x)=\frac{8}{9}$、$P(病気|x)=\frac{1}{9}$を当てはめてみる。
r(健康|x) = 0 \times \frac{8}{9} + 20 \times \frac{1}{9} = \frac{20}{9} \\
r(病気|x) = 1 \times \frac{8}{9} + 0 \times \frac{1}{9} = \frac{8}{9}
損失の期待値の当然小さい方が好ましいので、この場合$r(病気|x)$、即ち喫煙・飲酒共にするケースは「健康でない」と判断したほうがよくなり、先程とは異なる結果になる。
微妙なケースにおける判断の棄却
$C_{1}$に識別する確率も$C_{2}$に識別する確率も等しい場合、判断が正しいかどうかは五分五分になる。
こうした微妙なケースでは判断を避けることをリジェクトという。$x$について判断を誤る確率(誤り率)を$\epsilon$とし、これが閾値$t$以下であるようにすると考える($t$は誤り率の閾値であるため、逆に考えれば$1-t$より大きい確率で判断を下せるかが問題になる)。
このリジェクト基準を導入した場合、識別クラスは以下のように判断することになる。
C_{i}: \max_{j}P(C_{j}|x) > 1-t の場合 \\
リジェクト: \min_{j}P(C_{j}|x) <= 1-t
$1-t$より大きい確率で識別できるならOK、そうでないなら(どのクラスについても$1-t$以下でしか判断できない)ならリジェクト、となる。
モデルの評価
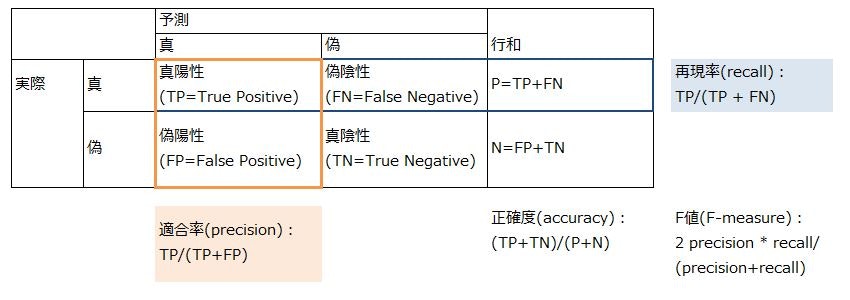
作成したモデルを評価するための指標として、混同行列(confusion matrix)がある。
precisionとrecallはトレードオフの関係にある。
正確な予測を行うために事後確率が高い時しか真と判定しないようにすると(識別境界を上げる)、真と予測したもののうち本当に真であるものの割合(precision)は上昇する。
しかし、一方で本当は真であったケースを多く見逃すことになりrecallが低下する。逆に、なるべく真のケースを見逃さないようにしようとするとこれと逆のことが起こる。
上記のデータで言えば、本当に病気の人しか病気と言わないようにするか(precision優先)、とりあえず病気っぽい人はみんな病気にしてしまうか(recall優先)というトレードオフになる。
F値はこのトレードオフをうまく調整した場合に上昇するようになっており(調和平均)、モデルの性能評価に使える指標となっている。
このトレードオフは偽陽性(FP)と真陽性(TP)の関係にも表れる(recallを上げると真と予想するケースが増え、偽陽性が増える)。よって、この2つの値の関係を見ることでもモデルの評価が可能である。
2つの値をプロットしたものをROC曲線(receiver operator characteristics curve)と呼ぶ。ROC曲線の下側の面積をAUC(area under an ROC curve)と呼び、これがモデル評価の指標となる(最良なら1.0。なぜなら、最良の場合偽陽性が0、真陽性が1になるため、1*1の正方形の面積になる)。
ただ、ROC曲線自体はモデルの良し悪しを教えてくれるものの、識別境界をどこにしたらいいかは教えてくれない。識別境界を決定するには、損失の期待値を同平面上にプロットするなどして最適な動作点を見つけることが必要である。