今日のテーマは「定常性、自己相関、相互相関、エルゴード性」。
定常性
定常性は時系列データを解析するための基礎になるもの。時系列データを前処理し、見出した定常性からモデルを構築する。そのモデルを元に、非定常性なモデルを構築する。
定常性は弱定常性と強定常性の2種類がある。
弱定常性
時間変化しても平均と分散、共分散(2次モーメントまで)が変化しない。
E(y_n) = E(y_{n+k})\\
Cov(y_n,y_m) = Cov(y_{n+k},y_{m+k})\\
Var(y_n) = Var(y_{n+k})
強定常性
時間変化しても確率分布(n次モーメントまで)が変化しない。
強定常性と弱定常性の関係について
強定常性が成立する時、弱定常性を必ず満たすとは限らない。
例1
コーシー分布などの一部の分布の場合、強定常性を満たすが弱定常性は満たさない。
理由:コーシー分布の場合、平均と分散は存在しないため、弱定常性の定義は満たさない。
例2
正規分布の場合、弱定常性を満たすなら、強定常性も満たす。
理由:正規分布は平均と分散が確定すると、確率分布の形が確定するから。
例3
平均、分散、共分散が存在する場合、強定常性を満たすなら、弱定常性を満たす。
自己共分散関数
時刻nの時系列データと時刻n+kの時系列データの共分散を求めたもの。
+kの事をlag(ラグ)と呼ぶ。
自己共分散の性質1
$C_k = C_{-k}$
lagをkと-kしたものは対象になる。つまり、左右対称。
自己共分散の性質2
$|C_k| \leqq C_0$
lagが0の時の共分散が最大になる。
自己共分散の性質3
非負定値性
\sum_{i=1}^{m}\sum_{j=1}^{m} \alpha_i \alpha_j C_{i-j} \geqq 0
Yule-Walker方程式が解を持つ性質がある
正直よくわからない。
自己相関関数
\\
R_{n,n-k} = \frac{Cov(y_n, y_{n-k})}{\sqrt{Var(y_n)}\sqrt{Var(y_{n-k})}}
\\
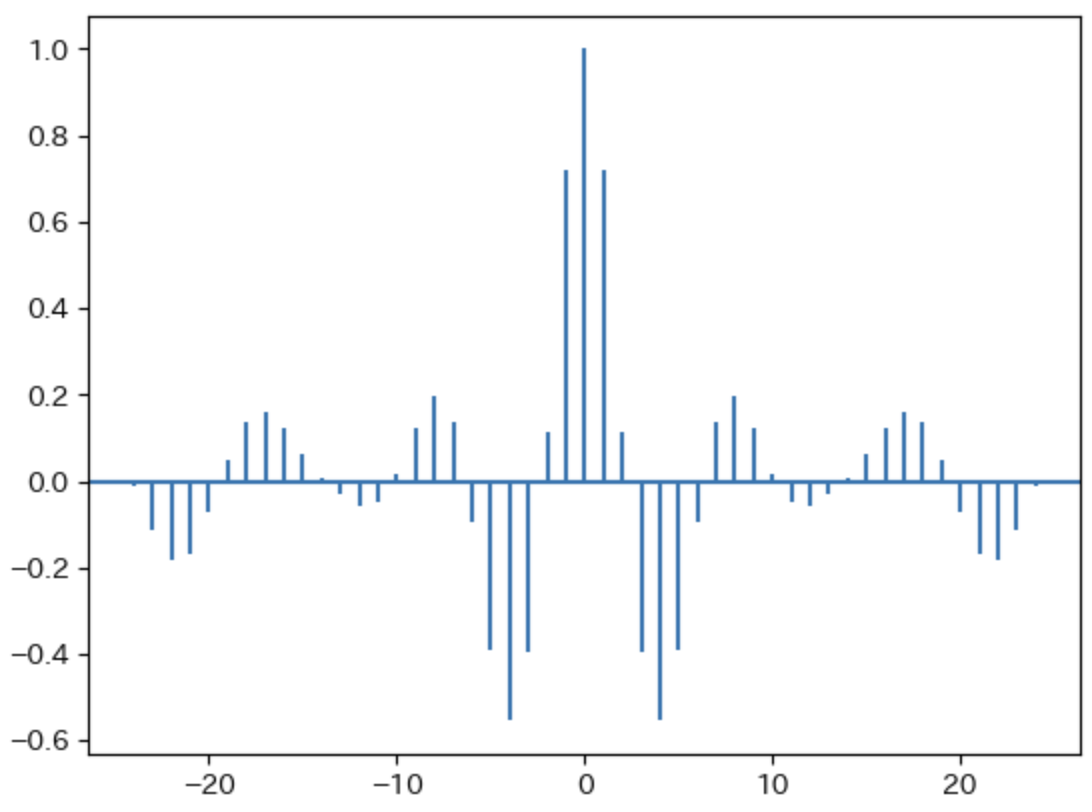
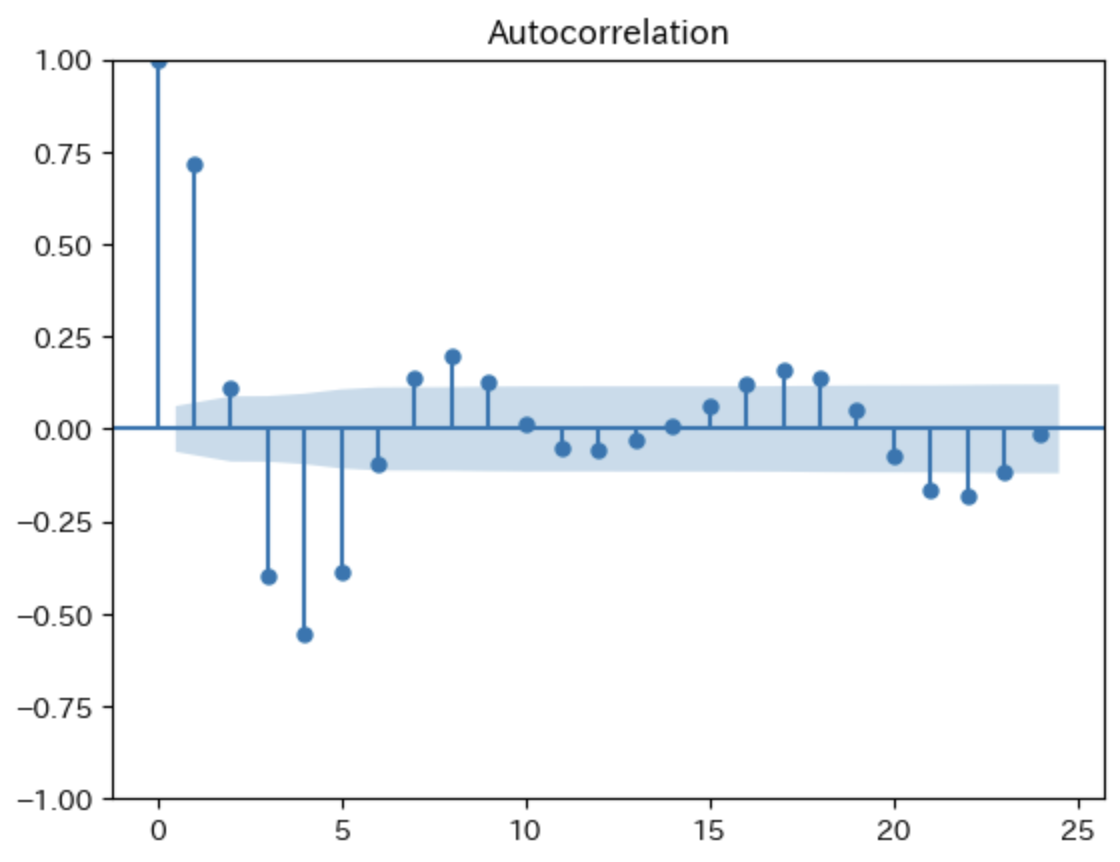
k = 0, ±1, ±2, ・・・, ±Lとラグを推移させ、自己相関を計算し、図示したものをコレログラムと呼ぶ。
コレログラムを作る方法①
from matplotlib import mlab
import matplotlib.pyplot as plt
# 自己相関のコレログラム(自己相関関数)の作成
num = 24
acorr_value = plt.acorr(df.方向角速度,
detrend=mlab.detrend_linear,
maxlags = num)
# plt.xlim(-1) 自己相関や自己共分散関数が左右対称なため、0以降の値のみでいい場合はこの項を有効にする。
plt.show()
ラグが k = 0 の時は、自己相関は常に1になる。
引数のdetrendについて
トレンドを除去するための引数。トレンド除去とは元データを平均を減算すること。
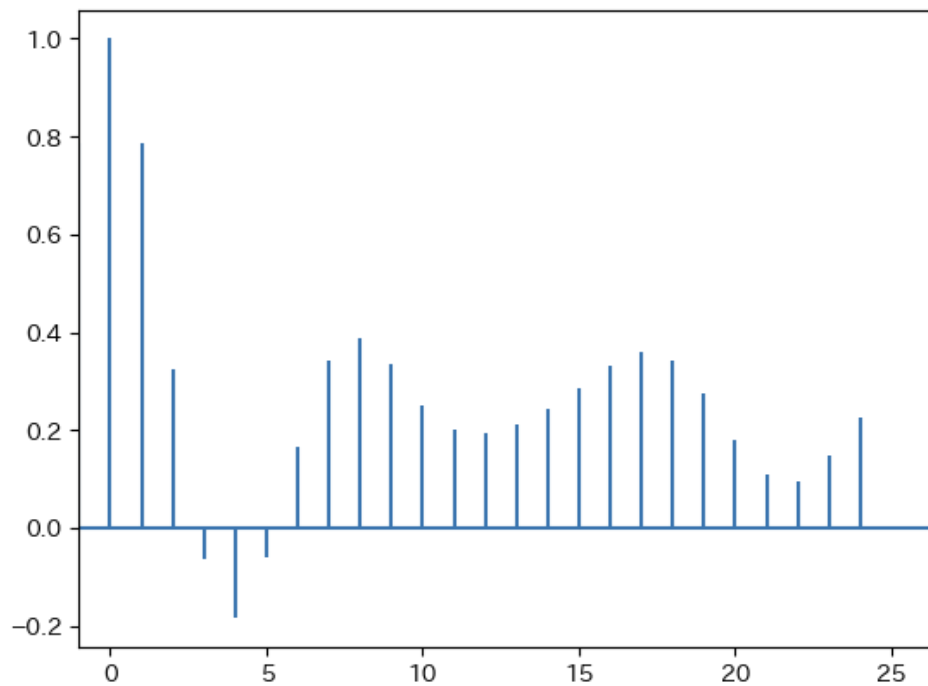
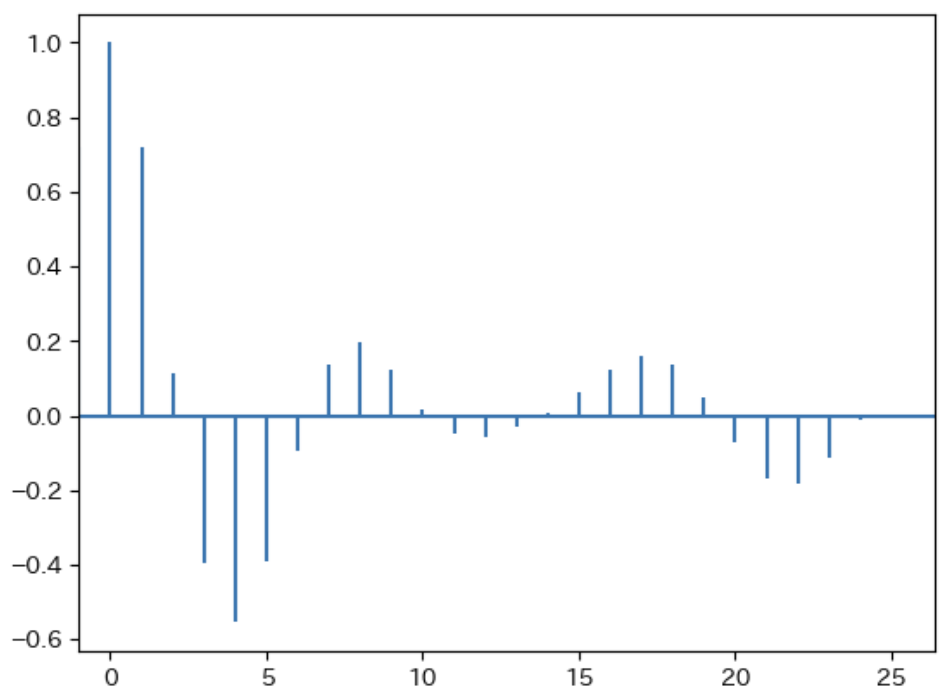
以下具体的に説明するために、まずdetrendがない場合とある場合を比べる。
# コレログラムの作成
num = 24
x = df.方向角速度
acorr_value = plt.acorr(x,
maxlags = num)
plt.xlim(-1)
plt.show()
# コレログラムの作成
num = 24
x = df.方向角速度
acorr_value = plt.acorr(x,
detrend=mlab.detrend_linear,
maxlags = num)
plt.xlim(-1)
plt.show()
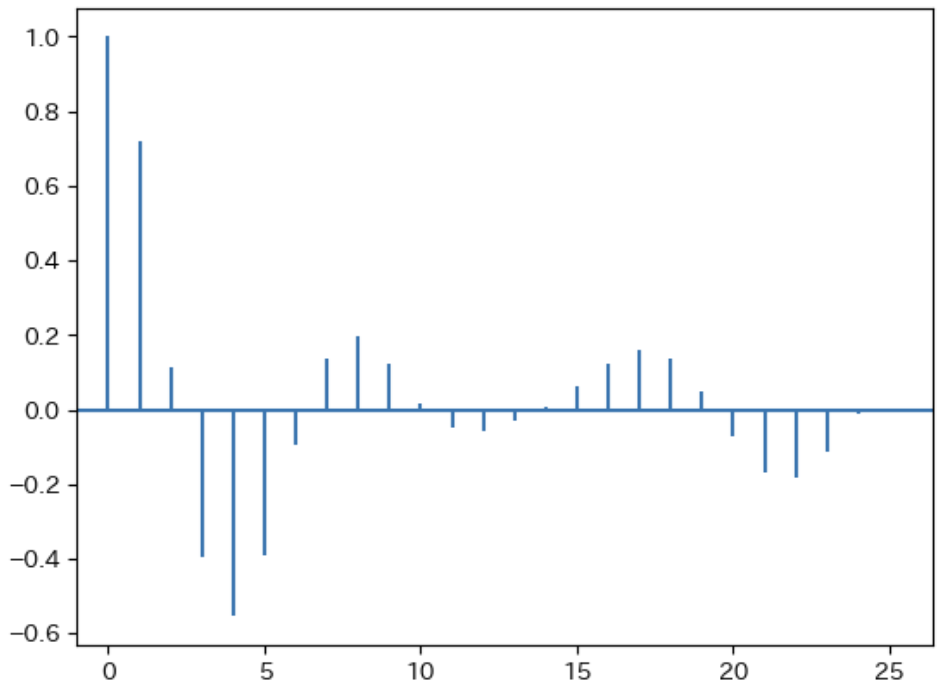
次に、detrendがなく、利用する時系列データから平均を引き算したデータを利用する。すると引数detrendを利用したときのコレログラムと同じグラフになることから、detrendのトレンド除去とは元データを平均を減算することだとわかる。
num = 24
x = df.方向角速度 - df.方向角速度.mean()
acorr_value = plt.acorr(x,
maxlags = num)
plt.xlim(-1)
plt.show()
コレログラムを作る方法②
statsmodelsを用いる。
import statsmodels.api as sm
sm.graphics.tsa.plot_acf(df.方向角速度, lags=24)
plt.show()
青帯はおそらく自己相関を0とした時の95%信頼区間を示していると思われる。
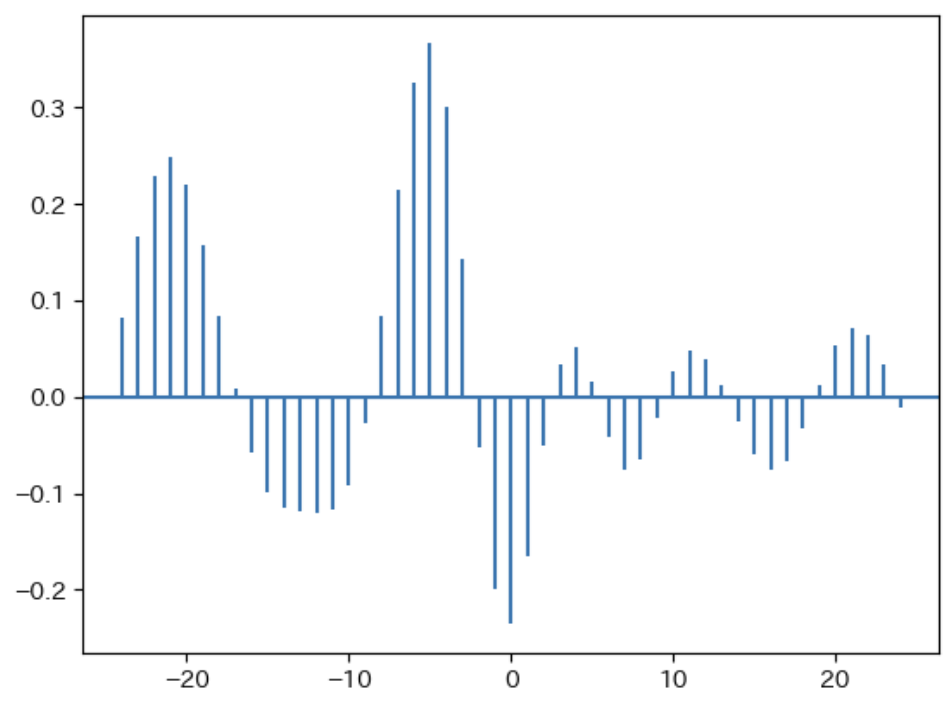
相互相関
異なる時系列データ同士の相関のこと。左右対称とはならないことに注意。
# 相互相関係数
xcor_value = plt.xcorr(df.方向角速度,
df.舵角,
detrend=mlab.detrend_linear,
maxlags=24)
plt.show()
エルゴート性
期待値(空間平均) = 時間平均 という性質。
時系列にはこの性質を仮定して分析を行う。
空間平均とは、仮に時刻nで何度もデータをサンプルできるとした時、その平均の値のこと。
時間空間とは、時系列データ全体の平均のこと。
おそらく時系列データが時刻nピンポイントで見ても、時間全体で見ても確率分布に従いると仮定したいのかもしれない。
参考にしたサイト