前回ARモデルを利用して時系列予測モデルを構築しましたが、今回はそれに引き続きARIMAモデルを利用して予測モデルを構築します。当記事は当記事内で完結します。
概要
・kaggleのデータセットを利用し、時系列の電力需要予測モデルをARIMAモデルで構築
・モデルを利用する前のデータの可視化やモデルの次数の決め方などARIMAモデル適用時の全体の流れを大雑把に書いた記事。
・ARIMAモデルはAR部分とI部分、MA部分に分解でき、p,d,qの3つのハイパラメータがある。
・ARIMA(p,d,q)の数式 : $y_{t} - y_{t-d} = b_{0} + b_{1}*\sum_{i}^{p}b_{i}y_{t-i} + \sum_{i}^{q}b_{i}\theta_{t-i} + \epsilon $
・AR部分($b_{0} + b_{1}*\sum_{i}^{p}b_{i}y_{t-i}$)はp期前までの時系列の値で現在の値を説明する部分
・I部分($y_{t} - y_{t-d}$)は階差をとって、モデルで説明する部分を定常性の形にしているもの。時系列は階差や対数階差、2回階差を取ることで定常性を発現することがある。
・MA部分($\sum_{i}^{q}b_{i}\theta_{t-i}$)は過去の誤差が現在に与えている影響を説明する部分。インパルスとも呼ばれる。
データセット
Prediction of electric power
Let's share code and approaches so as to improve our data-science skill each other.
import
import statsmodels.api as sm
import pmdarima as pm
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
前処理
train = pd.read_csv('data/train_df.csv')
train['DATE'] = pd.to_datetime(train.DATE)
group_train = train.groupby('DATE').mean()
group_train.sort_values(by='DATE', inplace=True)
# 訓練データとテストデータを準備
len_test = 24
df_train = group_train.POWER[:len(group_train) -len_test]
df_test = group_train.POWER[len(group_train)-len_test:]
予測モデル構築
1,データ全体を可視化
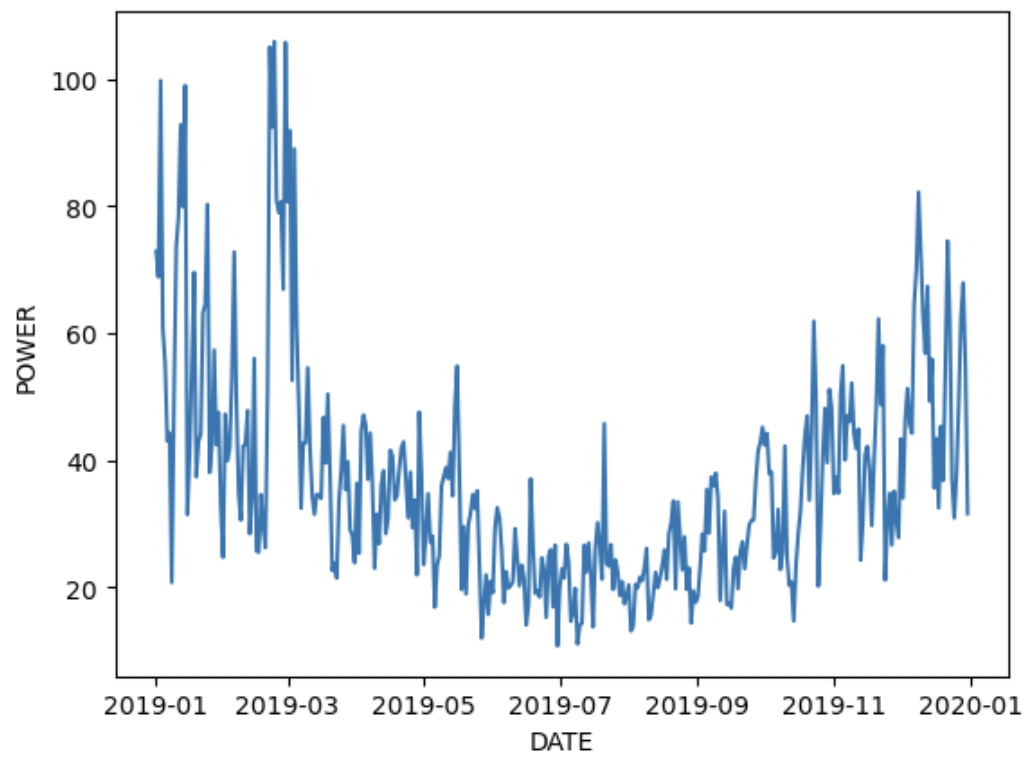
sns.lineplot(group_train.POWER)
時系列全体を確認する
階差をとった場合どうなるのかも確認する
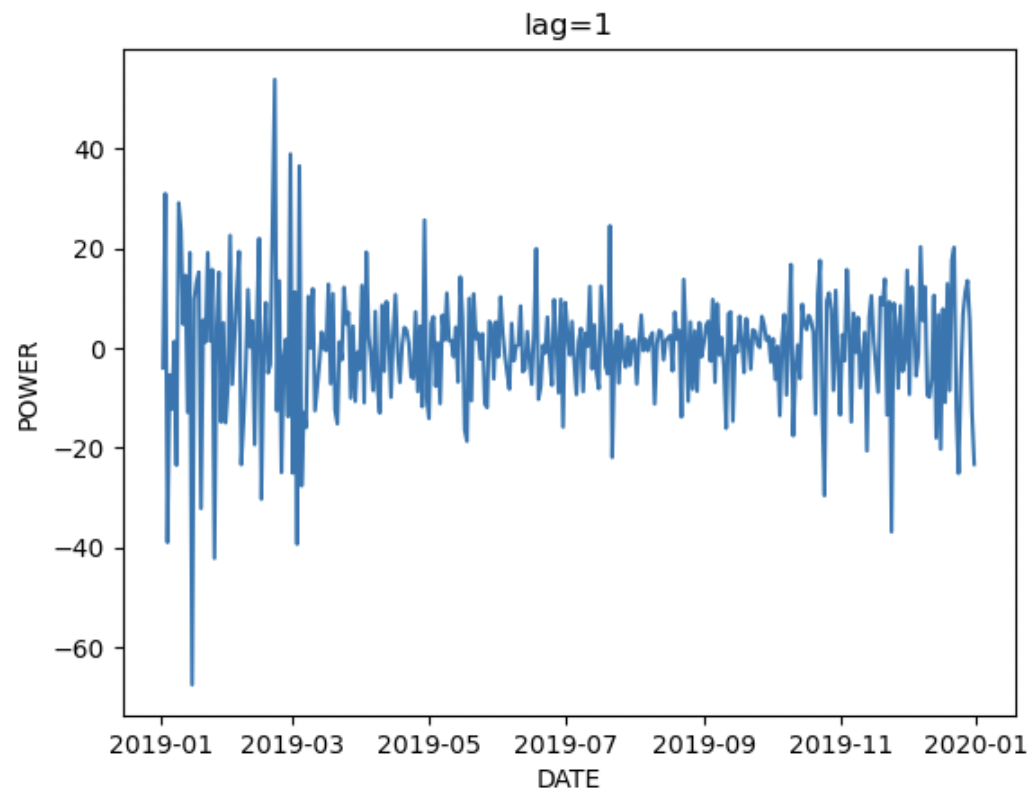
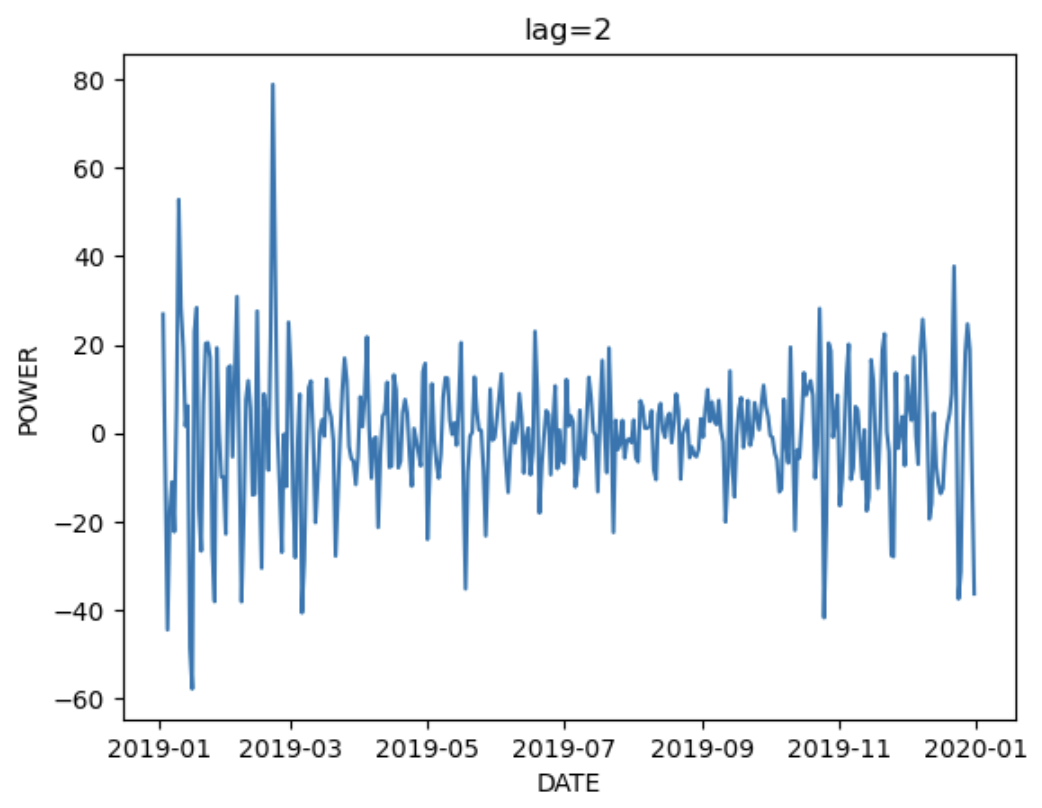
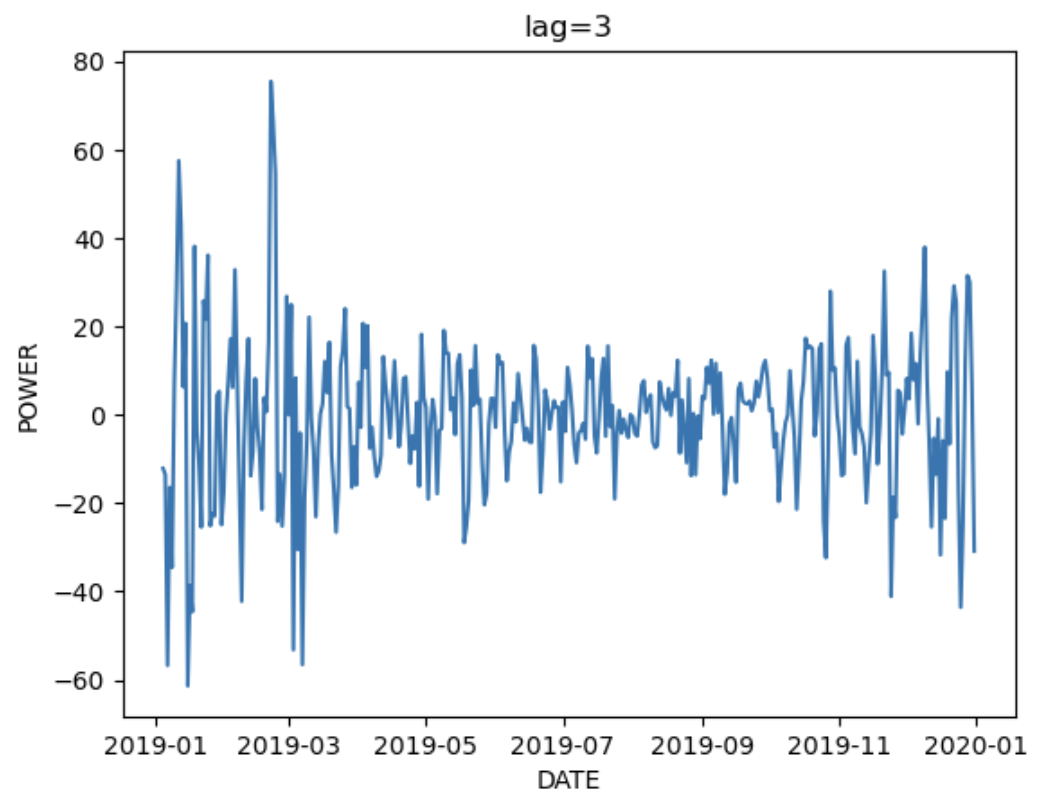
for i in [1,2,3]:
plt.title(f'lag={i}')
sns.lineplot(group_train.POWER.diff(i))
plt.show()
lag=1,2,3であまり形は変わらないのでARIMAモデルの階差部分の調整は時間をかけなくてもいいかもしれない。
また、階差をとっても分散が一定ではないので定常性は満たさないことがわかる。定常性を確認するにはディッキフラー検定を利用する。ARIMAモデル適用時には階差をとった時、定常性があった方がいいので今回の結果は微妙になると推測できる。
2,自己相関、偏自己相関の確認
#自己相関係数のプロット
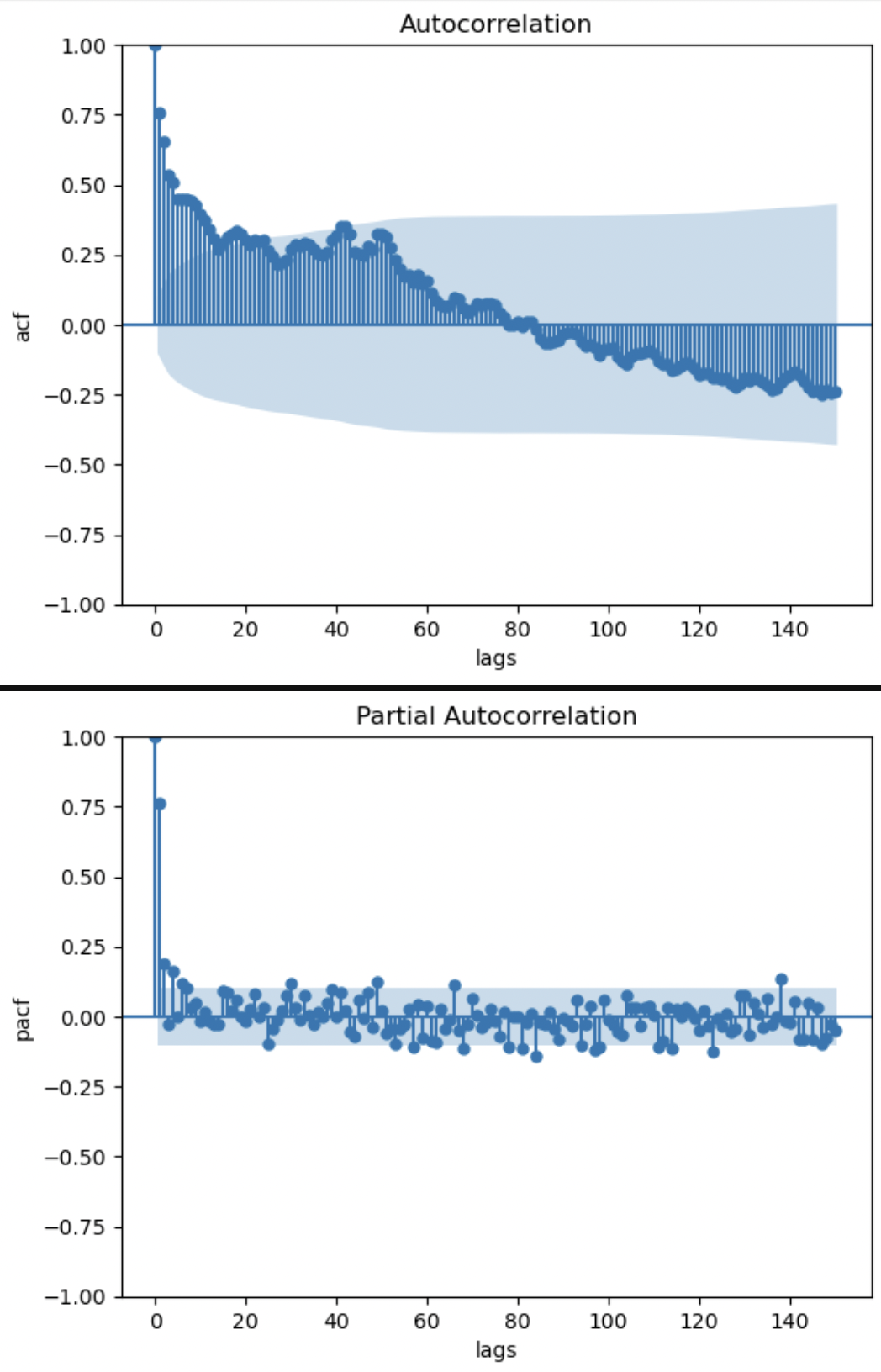
sm.graphics.tsa.plot_acf(group_train.POWER, lags=150)
plt.xlabel('lags')
plt.ylabel('acf')
#偏自己相関係数のプロット
sm.graphics.tsa.plot_pacf(group_train.POWER, lags=150)
plt.xlabel('lags')
plt.ylabel('pacf')
acf(上図)よりMAモデルの次数は15、6前後が妥当かもしれない。
また、pacfよりARモデルの次数は3あたりが妥当か?
ただし、次数の少ない無駄のないモデルが望ましい(過剰適合しないから、モデルの寿命が伸びるから)ことを考える必要がある。実践時系列解析によると、ARIMA(p,d,q)の次数それぞれは(5,3,5)あたりをオーバーするなら経験上無駄の多いモデルであると言えるそ雨なのでMA部分の次数が15は大きすぎる。
3,モデルの次数の決定(グリッドサーチで、基準:AIC)
# グリッドサーチで最適な次数を探す、基準はAIC
# パラメータの範囲を指定
p = range(0, 4) # AR次数の範囲
d = range(0, 1) # 階差の次数の範囲
q = range(0, 20) # MA次数の範囲
# パラメータの組み合わせを作成
parameters = [(i, j, k) for i in p for j in d for k in q]
# 最良のモデルを保持するための変数を初期化
best_aic = np.inf
best_order = None
# 各パラメータの組み合わせごとにモデルを評価し、最良のモデルを選択
for order in parameters:
try:
model = sm.tsa.SARIMAX(df_train, order=order)
model_fit = model.fit(disp=False)
if model_fit.aic < best_aic:
best_aic = model_fit.aic
best_order = order
except:
continue
print(best_order)
# (1, 0, 5)
先ほど、階差や自己相関のグラフをもとに探索範囲を決定する。
注意点として、探索範囲を広げすぎると計算量が2重に増える(計算範囲はpdq,モデルの次数が増えると計算時間がめちゃくちゃかかるの2重)ので注意。
今回はAICを基準にモデルのハイパラを決定する(値が小さいほど良い)
AIC = -2*(対数尤度) + 2*k
対数尤度はモデルの当てはまりの良さを計算したもの、kはパラメータの数。
数式をよくみると、パラメータの数が罰則項のような役割を果たしている。
どういうことかというと、パラメータの数を増やすとデータに対する当てはまりが良くなり(過剰適合する)、対数尤度が大きくなる。その結果右辺第1項の値が小さくなりAICの全体の値が小さくなるが、パラメータの数も多いので右辺第2項の値が大きくなりAIC全体の値が大きくなってしまうということである。
4,モデルの予測結果の可視化
グリッドサーチの結果をもとにモデルを構築し、予測結果を表示する。
model = sm.tsa.SARIMAX(df_train, order=best_order)
result = model.fit(disp=False)
result.aic
AIC:2604
fig, ax = plt.subplots(figsize=(20, 6))
min_lag = get_key_with_min_value(results_list)[0] + 1
forecast = result.forecast(len_test)
forecast.index = df_test.index
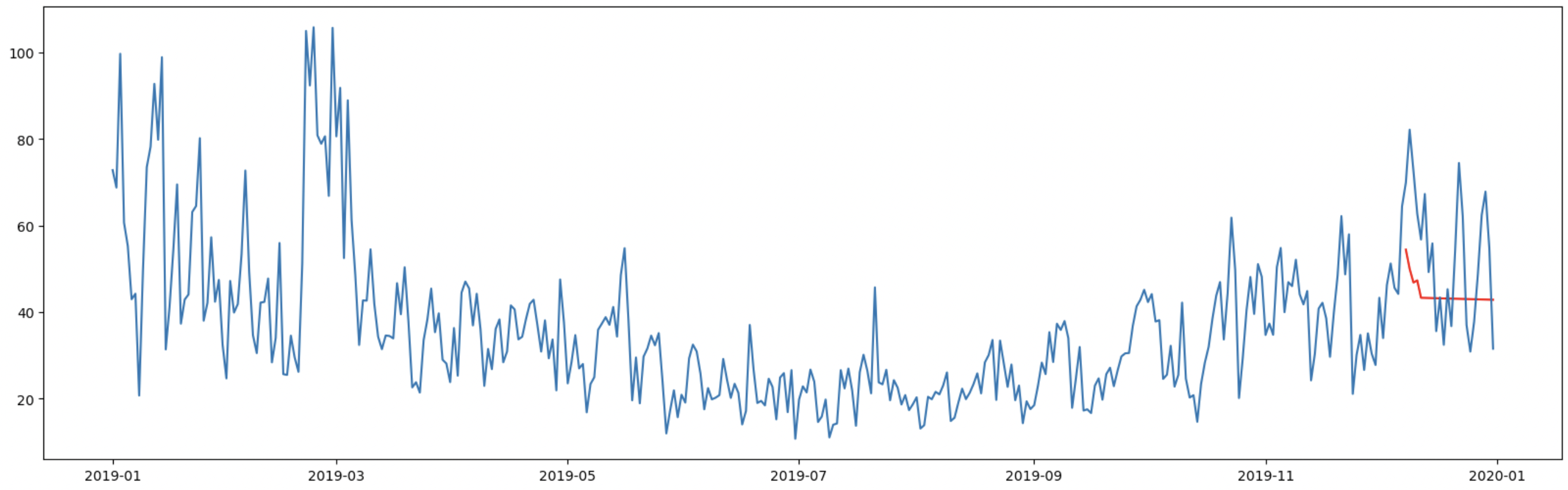
ax.plot(forecast, ls="-", color="r", label="predicted")
ax.plot(group_train.POWER, ls="-")
結果を見るとうまくいっていないことがわかる。
うまくいかなかった原因は階差をとってもデータに定常性がなかったことが原因ではないかと考えられる。
おまけ:モデルの次数をめちゃくちゃ増やして過剰適合させると
model = sm.tsa.SARIMAX(df_train, order=(130,1,10))
result = model.fit(disp=False)
fig, ax = plt.subplots(figsize=(20, 6))
min_lag = get_key_with_min_value(results_list)[0] + 1
forecast = result.forecast(len_test)
forecast.index = df_test.index
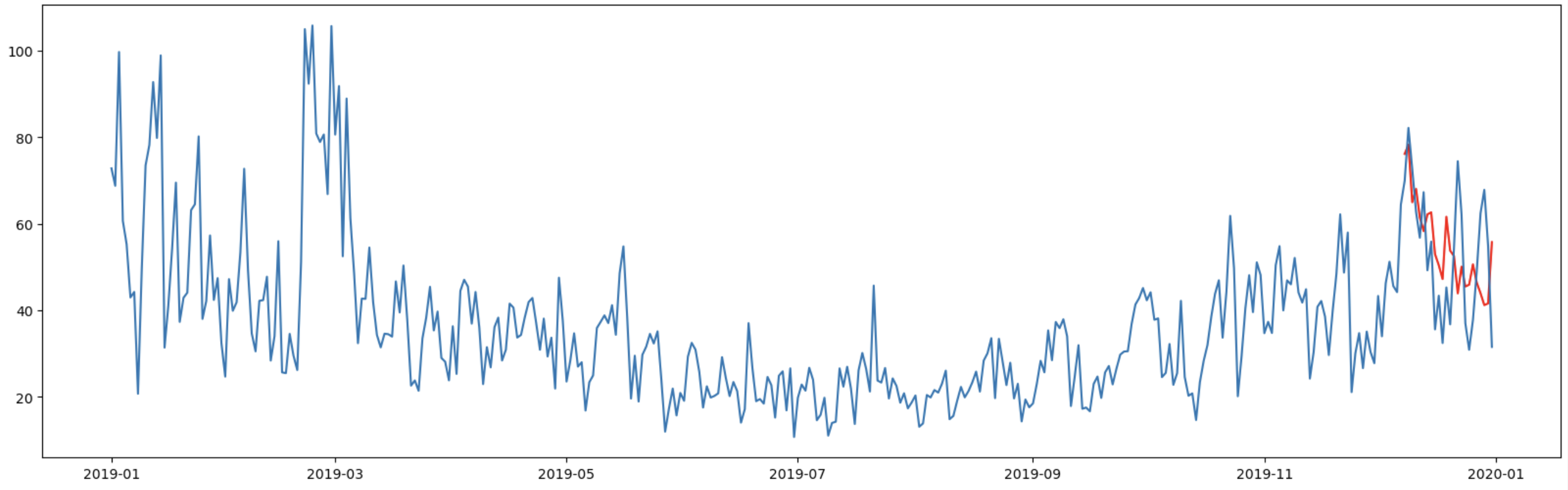
ax.plot(forecast, ls="-", color="r", label="predicted")
ax.plot(group_train.POWER, ls="-")
AIC:2700
予測の初めの方はしっかり予測できているが、後半の方はうまく予測できていないことがわかる。モデルを複雑にした割にはうまく説明できていないことがわかる。
参考文献
auto_ARIMAについて
今回利用したARTMA
実践時系列解析、オライリー