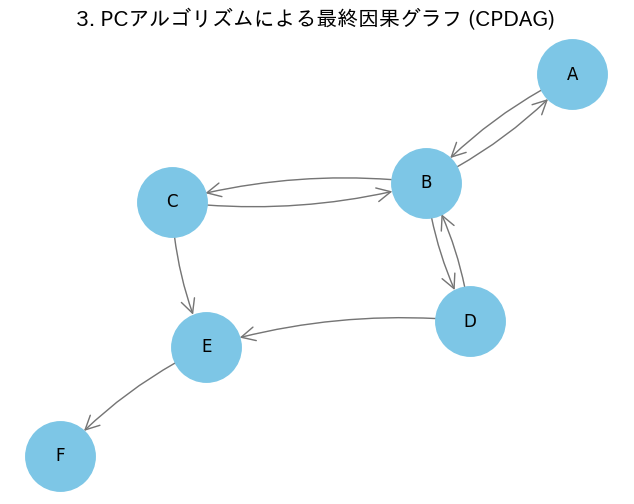
概要
はじめに
因果推論や因果探索を考える上で、重要な変数同士のパターンが3つある。
コライダー(合流点)やチェーン(連鎖)、フォーク(交絡変数)と呼ばれるものだ。
今日はコライダーとフォークに焦点を当て、なぜこのような考え方をすると因果推論がうまくいくのかを説明する。
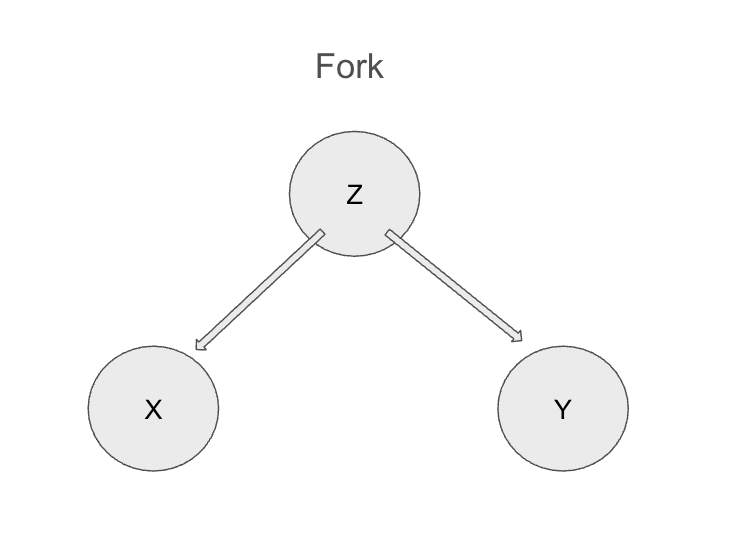
フォーク(交絡変数)とは
一つの変数 Z が他の二つの変数 X と Y の共通の原因となっている状態を指す。
図
例
夏の気温 (Z) が上がると、アイスクリームの売上 (X) も増え、水難事故の件数 (Y) も増える。この場合、アイスクリームと水難事故の間には直接的な因果関係はない。しかし、気温という共通原因によって相関が見える(偽相関)。
これが統計学者が口を酸っぱくして言っている「相関関係は因果関係ではない」ということだ。
分析をする際には夏の気温という交絡変数を統制する必要がある。
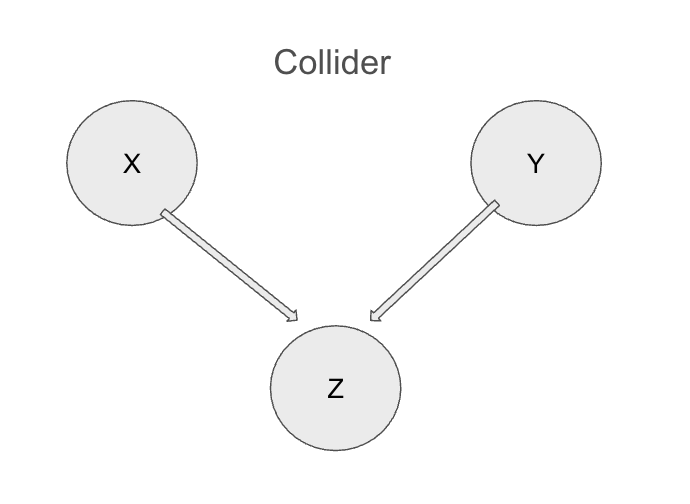
コライダー(合流点)とは
二つの変数 X と Y が一つの変数 Z の共通の結果となっている状態を指す。
図
例
大学入試の合格者 (Z) は、学力 (X) と運動能力 (Y) の両方が高い人が多いとします。学力と運動能力は本来独立であるとしても、合格者という集団に絞ると、学力が低い人の中では運動能力が高い人が多く、運動能力が低い人の中では学力が高い人が多くなる、といった相関が誘導される可能性がある。
どういうことか図を使って説明する。
①まず、学力と運動能力に全く相関がないことを考える。以下の様な状態だ。
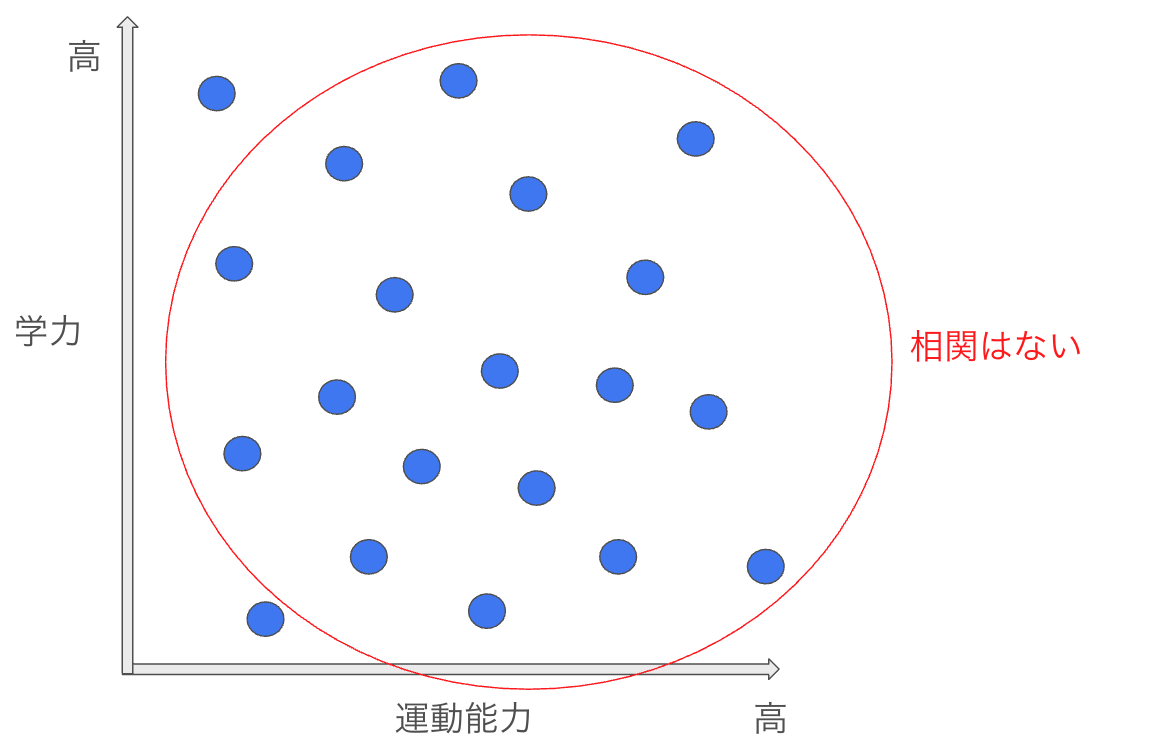
②ここに学力と運動能力の和が一定以上の場合、合格とすると以下のように合格者不合格者が別れる。
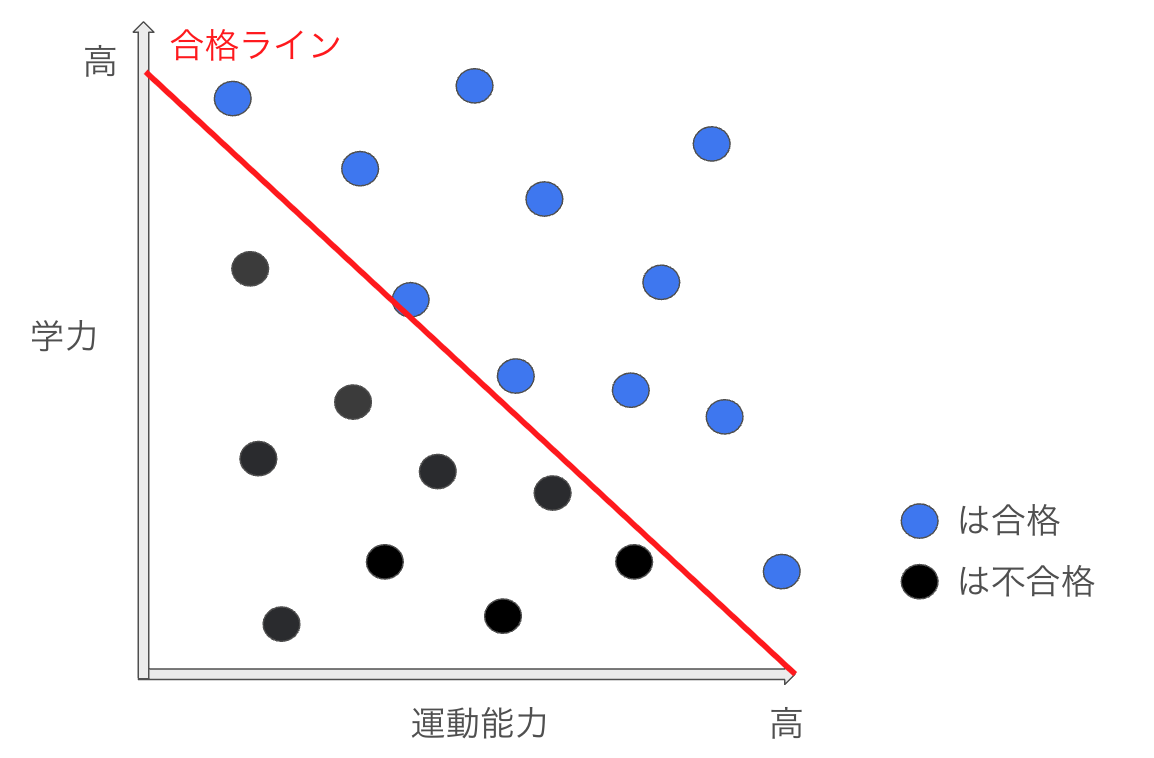
③大学合格者の中だけ見ると学力が高いほど運動能力が低いという負の相関が発生している様に見える。
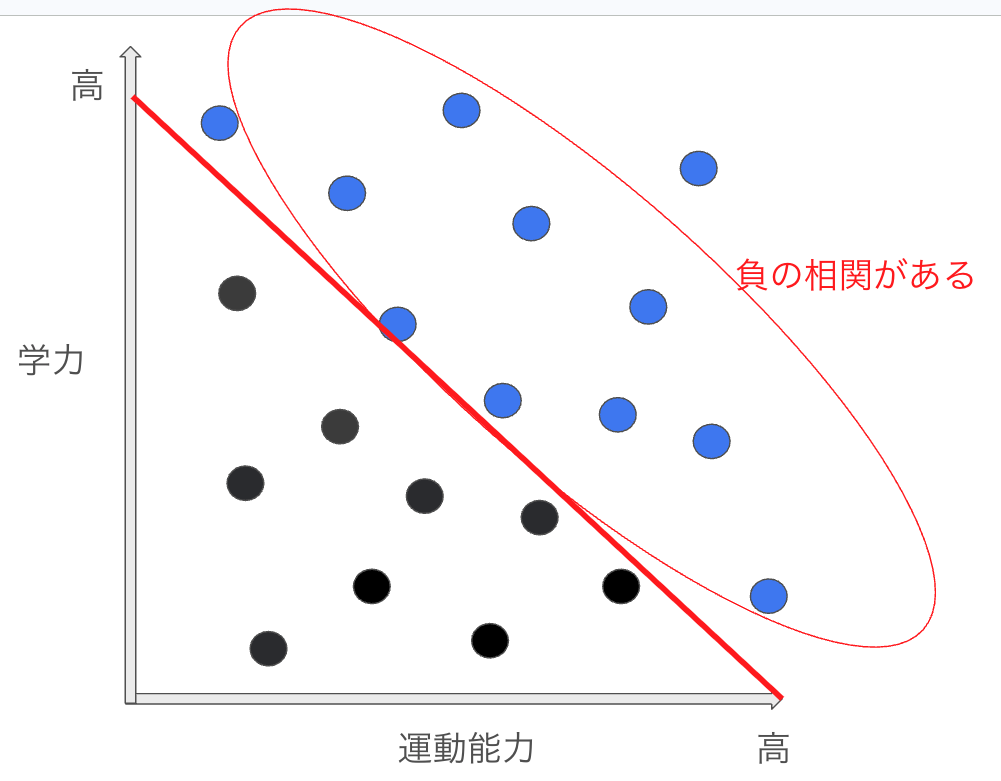
冗談だが、美人は性格が悪いという言葉も自身が何らかの基準線となり負の相関が見えているということなのかもしれない。
したがって、コライダーの変数に関しては統制すると偽相関が発生してしまうので、統制してはいけない。
以上、ここから先は本題のシミュレーションに入る。
シミュレーション
フォークのシミュレーションに関しては相関係数と偏相関係数を確認する。
偏相関係数
偏相関係数とはある変数Zを条件づけたときのXとYの相関を計算するためのもの。
r_{XY \cdot Z} = \frac{r_{XY} - r_{XZ} r_{YZ}}{\sqrt{(1 - r_{XZ}^2)(1 - r_{YZ}^2)}}
フォークのシミュレーション
import
import numpy as np
import pandas as pd
import pingouin as pg
import matplotlib.pyplot as plt
import seaborn as sns
simulation code
# シード値を設定して再現性を確保
np.random.seed(42)
# --- 1. フォークの状態のシミュレーション ---
print("--- フォークの状態のシミュレーション ---")
# Zを共通の原因として生成
Z_fork = np.random.normal(loc=0, scale=1, size=1000)
# XとYをZに依存させて生成 (ノイズを加える)
X_fork = 0.7 * Z_fork + np.random.normal(loc=0, scale=0.5, size=1000)
Y_fork = 0.6 * Z_fork + np.random.normal(loc=0, scale=0.5, size=1000)
# データフレームの作成
df_fork = pd.DataFrame({'X': X_fork, 'Y': Y_fork, 'Z': Z_fork})
# XとYの間の単純相関係数
corr_XY_fork = df_fork['X'].corr(df_fork['Y'])
print(f"フォークの状態における X と Y の単純相関係数: {corr_XY_fork:.4f}")
# XとYの間のZを調整した偏相関係数
partial_corr_XY_Z_fork = pg.partial_corr(data=df_fork, x='X', y='Y', covar='Z')['r'][0]
print(f"フォークの状態における X と Y の Z を調整した偏相関係数: {partial_corr_XY_Z_fork:.4f}")
出力結果
--- フォークの状態のシミュレーション ---
フォークの状態における X と Y の単純相関係数: 0.6145
フォークの状態における X と Y の Z を調整した偏相関係数: -0.0103
以上より、フォークの状態において、XとYは変数Zによって偽相関が発生していたが、変数Zを統制する偏相関係数を計算すると、Zがコントロールされることにより、相関がほぼ0となかったことが示された。
余談だが、これがPCアルゴリズムなどの因果探索に使われている核の部分となっている。
次にコライダーの時に、あえて変数Zを統制して偽相関が発生するのを確認する。
コライダーのシミュレーション
import
フォークのシミュレーションの時と同様。
simulation code
# --- 2. コライダーの状態のシミュレーション ---
print("\n--- コライダーの状態のシミュレーション ---")
# XとYを独立に生成
X_collider = np.random.normal(loc=0, scale=1, size=1000)
Y_collider = np.random.normal(loc=0, scale=1, size=1000)
# ZをXとYのコライダーとして生成 (XとYに依存し、ノイズを加える)
Z_collider = 0.5 * X_collider + 0.5 * Y_collider + np.random.normal(loc=0, scale=0.5, size=1000)
# データフレームの作成
df_collider = pd.DataFrame({'X': X_collider, 'Y': Y_collider, 'Z': Z_collider})
# XとYの間の単純相関係数
corr_XY_collider = df_collider['X'].corr(df_collider['Y'])
print(f"コライダーの状態における X と Y の単純相関係数: {corr_XY_collider:.4f}")
# XとYの間のZを調整した偏相関係数
partial_corr_XY_Z_collider = pg.partial_corr(data=df_collider, x='X', y='Y', covar='Z')['r'][0]
print(f"コライダーの状態における X と Y の Z を調整した偏相関係数: {partial_corr_XY_Z_collider:.4f}")
出力結果
--- コライダーの状態のシミュレーション ---
コライダーの状態における X と Y の単純相関係数: 0.0192
コライダーの状態における X と Y の Z を調整した偏相関係数: -0.4890
以上より、XとYの単純な相関係数を見た時にはちゃんと相関はほぼ0となっているが、コライダーである変数Zを統制したXとYの偏相関係数を見ると、負の相関が発生していることがわかる。
PCアルゴリズム
偏相関の面白い性質を見たので、ついでにそれが深く関連する因果探索手法であるPCアルゴリズムについて簡単に説明する。
PCアルゴリズム全体の流れ
相関係数をベースに因果探索をするアルゴリズムの一種である。
別のアルゴリズムに関してはこちらを参照:
アルゴリズムの全体の流れの説明とともにシミュレーション結果を表示する。
まず、シミュレーション用のデータを生成する。
1、シミュレーション用データの生成
import
# !pip install causal-learn networkx matplotlib pandas numpy japanize-matplotlib
import numpy as np
import pandas as pd
import networkx as nx
import matplotlib.pyplot as plt
import japanize_matplotlib
from causallearn.search.ConstraintBased.PC import pc as PC
from causallearn.utils.GraphUtils import GraphUtils
generation
# シード値を設定して再現性を確保
np.random.seed(42)
# データ数
n_samples = 1000
# 変数の生成
# ノイズ項は標準正規分布からサンプリング
e_A = np.random.normal(0, 1, n_samples)
e_B = np.random.normal(0, 1, n_samples)
e_C = np.random.normal(0, 1, n_samples)
e_D = np.random.normal(0, 1, n_samples)
e_E = np.random.normal(0, 1, n_samples)
e_F = np.random.normal(0, 1, n_samples)
# 因果関係に基づいた変数の計算
A = e_A
B = 0.8 * A + e_B # A -> B
C = 0.7 * B + e_C # B -> C
D = 0.6 * B + e_D # B -> D
E = 0.7 * C + 0.6 * D + e_E # C -> E, D -> E (EはCとDのコライダー)
F = 0.9 * E + e_F # E -> F
# データフレームにまとめる
df = pd.DataFrame({
'A': A, 'B': B, 'C': C, 'D': D, 'E': E, 'F': F
})
print("生成されたデータの最初の5行:\n", df.head())
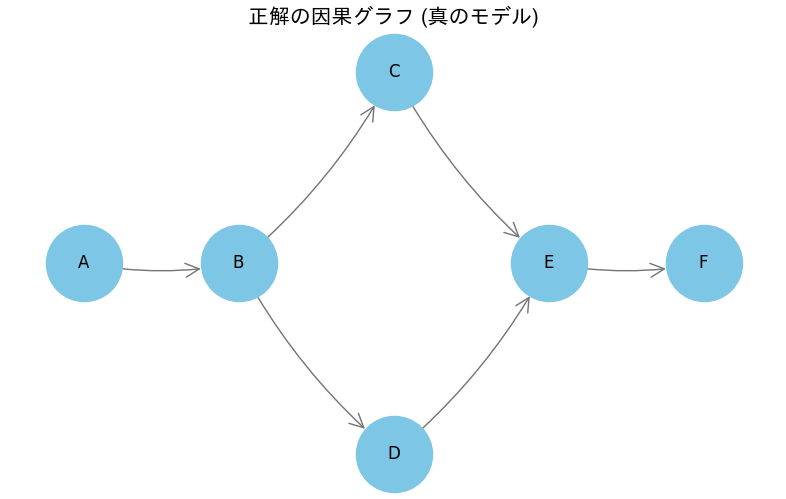
真の因果関係は以下の様になっている。
フォークやコライダーが存在していることがわかる。
# グラフ描画用の関数を定義
def plot_graph_fixed_layout(graph, title):
"""
NetworkXのグラフオブジェクトを受け取り、指定された因果の向きにレイアウトして描画する関数。
"""
plt.figure(figsize=(10, 6))
# 1. ★★★ここが重要★★★
# 因果の流れ(A→B→C/D→E→F)に沿って、各ノードの(x, y)座標を手動で設定
pos = {
'A': (0, 0),
'B': (1, 0),
'C': (2, 1), # Bから分岐して上へ
'D': (2, -1), # Bから分岐して下へ
'E': (3, 0), # CとDが合流
'F': (4, 0)
}
# 2. 描画のパラメータを設定
node_size = 3000
arrow_size = 25
node_color = 'skyblue'
edge_color = 'gray'
font_color = 'black'
font_size = 12
# 3. ノード、エッジ、ラベルをそれぞれ描画
nx.draw_networkx_nodes(graph, pos, node_size=node_size, node_color=node_color)
nx.draw_networkx_edges(
graph,
pos,
node_size=node_size,
arrowstyle='->',
arrowsize=arrow_size,
edge_color=edge_color,
connectionstyle='arc3,rad=0.1'
)
nx.draw_networkx_labels(graph, pos, font_size=font_size, font_color=font_color)
# 4. グラフのタイトルと表示設定
plt.title(title, size=15)
plt.axis('off')
# X軸の範囲を少し広げて、左右の余白を確保
plt.xlim(-0.5, 4.5)
plt.show()
nodes = ['A', 'B', 'C', 'D', 'E', 'F']
true_graph = nx.DiGraph()
true_graph.add_nodes_from(nodes)
true_graph.add_edge('A', 'B')
true_graph.add_edge('B', 'C')
true_graph.add_edge('B', 'D')
true_graph.add_edge('C', 'E')
true_graph.add_edge('D', 'E')
true_graph.add_edge('E', 'F')
# 修正した関数でグラフを描画
plot_graph_fixed_layout(true_graph, "正解の因果グラフ (真のモデル)")
2、スケルトンの構築
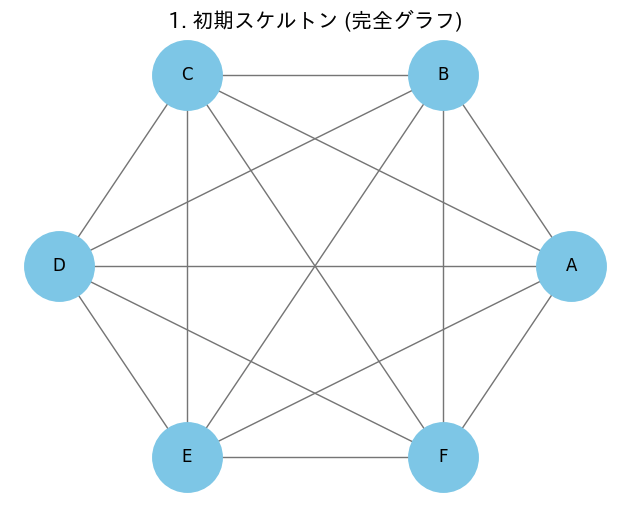
今回はシミュレーションデータからわかるように6つの変数が関係している状況を考える。
スケルトンとは骨格のことで、まずすべての変数を繋いだ図を考える。
# 完全グラフの生成
initial_graph = nx.Graph()
initial_graph.add_nodes_from(nodes)
for i in range(len(nodes)):
for j in range(i + 1, len(nodes)):
initial_graph.add_edge(nodes[i], nodes[j])
plot_graph(initial_graph, "1. 初期スケルトン (完全グラフ)")
3、0次条件付き独立性テスト
要するにシンプルな相関係数だけを見て関係を探る。
これにプラスして、条件付き独立性テストを用いて、独立か、それとも従属化を見ている。
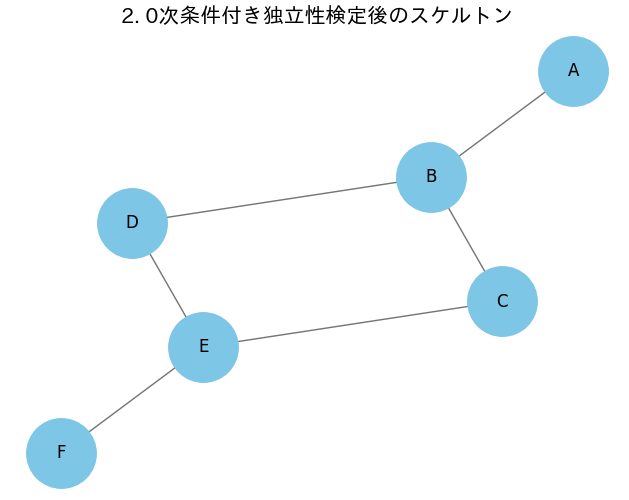
これらの手法を用いて、関係のないエッジを削除できる。結果以下のようになる。
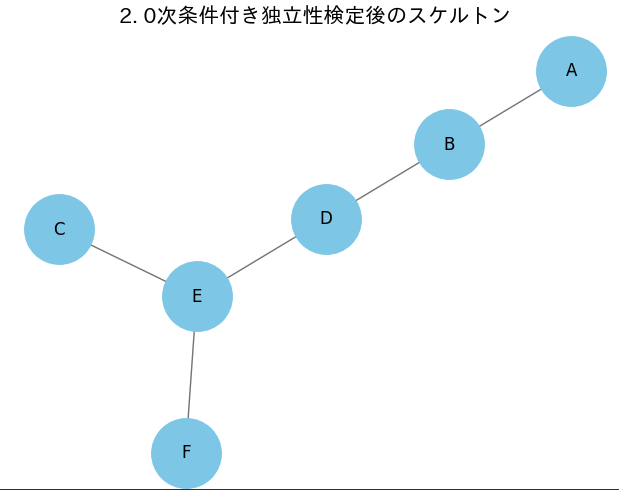
今回は概ねうまくいっており、後は因果の方向を考えるだけである。ただし、データ数が少ないなどの問題がある場合は以下の様なる可能性がある。
# PCアルゴリズムの実行 (max_k=0で0次条件付けのみを考慮)
cg_0_order = PC(data=df.values, alpha=0.05, indep_test='fisherz', max_k=0)
# causal-learnのCausalGraphオブジェクトからNetworkXのGraphに変換
graph_0_order_nx = nx.Graph()
graph_0_order_nx.add_nodes_from(nodes)
for i in range(len(nodes)):
for j in range(i + 1, len(nodes)):
if cg_0_order.G.graph[i, j] != 0 or cg_0_order.G.graph[j, i] != 0:
graph_0_order_nx.add_edge(nodes[i], nodes[j])
plot_graph(graph_0_order_nx, "2. 0次条件付き独立性検定後のスケルトン")
4、高次条件付き独立性テスト
要するに偏相関係数を見ています。例えば、コライダー(合流点)の場合、変数Zをコントロールすることで、相関が生じた様に見えます。つまり、0次の処理では独立だったものが、1次の処理で相関が生じる場合、それは合流点であると言えるわけです。
処理後の結果が以下になります。
一部因果の流れを特定できていない(矢印が双方向になっている部分)が、コライダーの部分に関しては因果の流れが特定できていることがわかる。
そのほかの部分については人間が論理性や先行研究等を活用して同定する必要がある。
補足として、ここでは先ほど挙げたようにZだけではなくZ、V、Wなどより多い変数で条件付けなどを行っています。
print("PCアルゴリズムを実行中...")
# PCアルゴリズムの実行
cg_final = PC(data=df.values, alpha=0.05, indep_test='fisherz')
print("PCアルゴリズム完了。")
# STEP 1: .to_nx_graph() を呼び出し、内部で変換を実行
cg_final.to_nx_graph()
# STEP 2: 変換結果が格納された .nx_graph 属性を取得
# この時点では、ノードは 0, 1, 2... という数字になっている
graph_with_integers = cg_final.nx_graph
# STEP 3: ノード名のマッピング辞書を作成
# {0: 'A', 1: 'B', 2: 'C', ...} という辞書を作る
nodes = df.columns.tolist()
labels = {i: name for i, name in enumerate(nodes)}
# STEP 4: nx.relabel_nodes() を使って、ノード名を数字からアルファベットに置換
final_graph_nx = nx.relabel_nodes(graph_with_integers, labels)
plot_graph(final_graph_nx, "3. PCアルゴリズムによる最終因果グラフ (CPDAG)")
PCアルゴリズムの前提条件
PCアルゴリズムが観測データから因果構造を推論するために必要となる、主要な前提条件を以下にまとめる。
1、因果的マルコフ条件
ある変数は、その直接の原因が与えられた条件下では、それ以外の(直接の原因ではない)変数から独立である。
因果推論におけるパータンの1つであるチェーンにも影響することですが、今回の記事では解説をしていません。
詳しくはこちらのスライドを参照して下さい。
2、忠実性条件
データにおける全ての条件付き独立性は、因果グラフの構造(d分離)によって説明できる(詳しくは参考文献参照)。
つまり、変数Zなどで条件づけしたときにちゃんと独立になることが前提となっている。
3、因果的十分性
分析に含まれる変数セットの中に、共通の原因を持つ全ての変数が含まれている。
別の言い方をすると、観測されていない隠れた変数(例: 生まれ持った能力、その日の気分など)が、分析対象の複数の変数に影響を与えている状況は存在しない、という強い仮定である。
噛み砕くと、因果に関係のある変数はすべて観測されている。
4、DAGであること
DAGとは有向非巡回グラフのことであり、因果の効果がループしないという前提である。例えば、XがYに影響して、YがさらにXに影響するみたいな状態が存在しないということである。
弱点
最後に弱点について言及する。
まず、1つ目として「相関は因果ではない。」と当記事の最初で言及したが、当アルゴリズムは相関からのみ因果を特定しようとしている。前提条件が全て揃っている場合にのみ相関から因果を特定することができるが、上記の4条件(特に1〜3)が揃っていることは現実世界では滅多になさそうである。特に未観測な交絡変数が存在しないという部分ネックだと思う。
2つ目に変数が多い場合、何度も条件付き独立性テストを行うことになるため、ボンフェロー二補正などのp値の調整が必要になる。
3つ目に因果の向きを完全に特定できることは稀であることだ。今回のシミュレーションでもわかった通り、一部の因果の流れを特定できなかった。
参考文献
Powered by Google AI Gemini Pro 2.5
d分離、バックドア基準について:
謝辞(Acknowledgment)
本記事の作成にあたり、Googleの生成AI『Gemini』を補助的に使用しました。