前半の概要
・データはRCTしたデータから一部のデータを抽出し、バイアスを持たせたものを利用。
・DR推定量を用いてメールマーケティングの因果効果を推定。
・DR法とIPW、傾向スコアによる最近傍マッチング法、重回帰分析と比較した結果、バイアスを大きく軽減できなかったので今回のデータでは良い推定量ではなかった。
後半の概要
・因果推論と機械学習の手法を融合させたDR-Linaerを利用し、ITE(indivisual treatment effect)を推定。
・ITEをモデル(ランダムフォレスト)に学習させることで、未知のデータに対して予測できるようにし、効果検証を実施。
・ITEをシミュレートすることで、今後のマーケティング施作に対して、2つ方向性を示した。
コード:https://github.com/harukicode0/Doubly_Robust_Estimator_Simulation
前半パート
DR推定量を用いてメールマーケティングの効果を検証
利用したデータについて
・Kevin Hillstrom:氏のホームページMineThatDataより、メール施作においてランダム化比較実験がなされたデータが利用。このデータからバイアスが生じるようにデータをフィルタリングしたものを分析する。
・各カラムについて下表を参照。
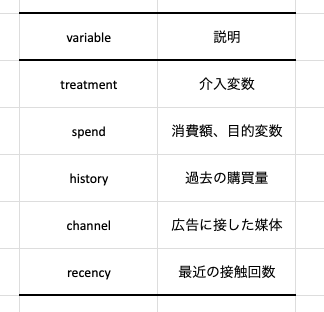
rct_df = pd.read_csv('http://www.minethatdata.com/Kevin_Hillstrom_MineThatData_E-MailAnalytics_DataMiningChallenge_2008.03.20.csv')
male_df = rct_df.query('segment != "Womens E-Mail"')
male_df['treatment'] = male_df.segment.apply(lambda x: 1 if x == 'Mens E-Mail' else 0)
male_df = pd.concat([male_df,
pd.get_dummies(male_df.channel,
drop_first=True,
prefix_sep='_',
prefix='channel')],
axis=1)
np.random.seed(1)
male_df['random_num'] = np.random.uniform(0,1,male_df.count()[0])
male_df['rate_c'] = 1.0
male_df['rate_t'] = 0.25
idxs = male_df.query('history > 300 & recency < 6').index
male_df.loc[idxs,'rate_c'] = 0.5
male_df.loc[idxs,'rate_t'] = 1
biased_data = pd.concat([male_df.query('treatment == 0 & random_num < rate_c'), male_df.query('treatment == 1 & random_num < rate_t')])
biased_data
DR推定量とは
傾向スコアによる重み付けと回帰モデルを用いて真の値を推定する手法。以下の2つの仮定のうち、少なくともどちらかが正しい場合、推定量はパラメータの一致推定量となる。
仮定1:傾向スコアを算出するモデルは正しい
仮定2:目的変数を算出するモデルは正しい
加えて、仮定1と2の両方を満たしている場合、DR推定量の漸近分散はIPWのよりも小さくなるという性質がある。
数式で今回利用する式を表現すると下記のようになる。
\mu_{DR} = \frac{1}{N}\sum_{i=1}^{N}\frac{D_{i}}{e(X_{i})}Y_{i} - \frac{1}{N}\sum_{i=1}^{N}(1-\frac{D_{i}}{e(X_{i})})Y^{m}_{i}
ここで
・Nはサンプル数
・$D^{i}$は介入変数
・$e(x^i)$は傾向スコア
・Yは目的変数の値。欠測している値はモデルによって予測したYで補完する。
ここでATEを求めるにはDR推定量の以下の2つの式の差分を求める。
まず、トリートメントグループのDR推定量
\mu^{DR}_1 = \frac{1}{N}\sum_{i=1}^{N}(\frac{D_{i}}{e(X_{i})}Y_{i1} - \frac{1}{N}(1-\frac{D_{i}}{e(X_{i})})Y^{m}_{i1})
次に、コントロールグループのDR推定量
\mu^{DR}_0 = \frac{1}{N}\sum_{i=1}^{N}(\frac{1 - D_{i}}{1 - e(X_{i})}Y_{i0} - \frac{1}{N}(1-\frac{1 - D_{i}}{1 - e(X_{i})})Y^{m}_{i0})
この時、ATEは$\mu^{DR}_1 - \mu^{DR}_0$で推定できる。
DR推定量を利用した因果推論の結果
| 推定方法 | 結果 |
|---|---|
| 真の値 | 0.7698 |
| DR推定量 | 0.6303 |
| 重回帰分析 | 0.7192 |
| 最近傍傾向スコアマッチング | 0.7627 |
| IPW | 0.6826 |
| 平均の差 | 0.9888 |
結果より今回のデータでは他手段よりうまく推定することができなかったことがわかる。
後半
DR推定量と機械学習の手法を融合し、マーケティング施作に対して提言をする。
やりたいこと
DR推定量を利用し、ITE(各個人の因果効果)を推定。
推定した結果をランダムフォレストに学習させ、未知の属性を持つ顧客に対してでもメールマーケティングの効果を予測できるようにする。
手順
1、コントロールグループのデータのみを用いて、介入がなかった場合の個人のメールマーケの効果量を学習。この時の作成したモデルをmodel0とする。
2、トリートメントグループのデータのみを用いて、介入があった場合の個人のメールマーケティングの効果量を学習。この時の作成したモデルをmodel1とする。
3、データを傾向スコアは用いて調整し、加えて1と2で作成したモデルを利用し、DR推定量の計算式で真の効果量を推定。
4、DR推定量を用いてすべての顧客のITEを計算。この際、反事実データをmodel1とmodel2モデルを用いて補完する。
5、ITEを学習させたモデル(model2)を作成し、未知の顧客に対して、介入した時の効果量を予測する。
DRーLinearとは
ITEを任意のモデルに学習させ、因果効果を予測する方法である。ITEを算出する際にDR推定量を利用する。また、欠損値補完にも機械学習を利用するので、合計3つの機械学習モデルを利用することになる。
ITEをモデルに学習させた結果
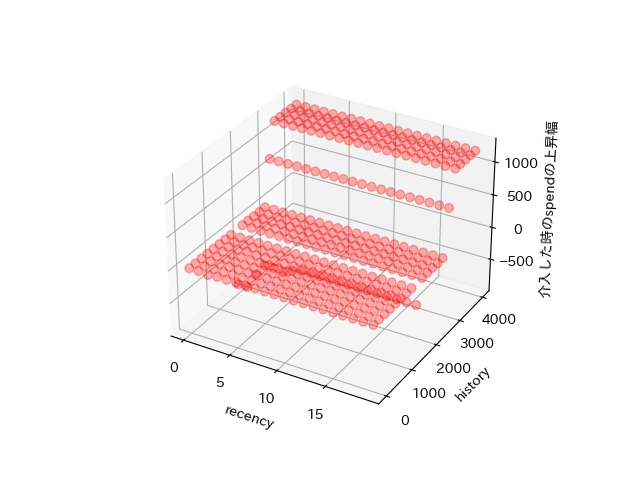
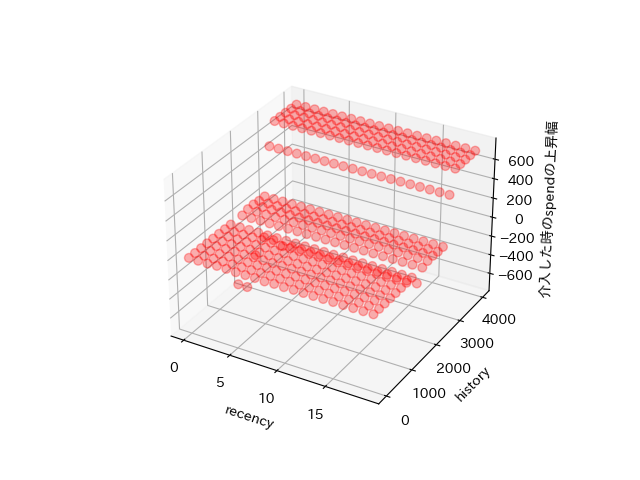
モデルに学習させ、recencyが0~20、historyが0~4000の間の顧客の各ITEがどのようになるか予測し、図示。
ここから今後のマーケティングに対して提言することができる。
結果からマーケティング施作に対して提言できること
結果より2つの戦略が考えられる。
①historyが2800,3000の境目で急激に消費量が増えている優良顧客がいる。これらの顧客に対してターゲットマーケを実施する戦略。
②historyが2000未満、かつrecencyが5以上の顧客に対してはマーケをすることで消費量が下がる傾向が見られるので、その層をターゲットとしたマーケティングはしない方が良い。したがって、recencyが5未満(つまり、最近接触が少ない顧客)に対して、幅広くマーケティングする戦略。
以上の知見が得られた。
参考文献
効果検証入門