KFold + OputnaでLightgbmをチューニングする

#初めに

Optunaでlightgbmをチューニングして回帰分析をしてみたので、その忘備録です。

使用したデータは、こちらのコンペ↓で使用されるデータです。
House Prices - Advanced Regression Techniques

こちらのコンペは住宅の売値を予測するコンペとなっています。
住宅の値段なので、築年数や広さが重要だと思いますが、初手は可能な限り特徴量を使う方向で行きます。

モデルの精度については、RMSE約0.124がベストスコアとなっており、kaggleにsubmitして算出された値になります。
この記事執筆時点では、大体上位17%あたりの順位でした。
コンペの評価基準にはRMSEが使用されています。

#準備

#今回使ったライブラリ
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
import warnings
warnings.filterwarnings("ignore")

from sklearn.model_selection import KFold, cross_validate
from sklearn.preprocessing import LabelEncoder
from sklearn.metrics import mean_squared_error as mse
import optuna
from optuna.visualization import plot_optimization_history, plot_param_importances
import lightgbm as lgb

次にデータの読み込みと欠損値のチェック。

train_data = pd.read_csv("house-prices-advanced-regression-techniques/train.csv")
train = train_data.copy()
train.index = train["Id"]
del train['Id']
test_data = pd.read_csv("house-prices-advanced-regression-techniques/test.csv")
test = test_data.copy()
test_id = test['Id']
test.index = test["Id"]
del test['Id']

#欠損値をカウントしたDataFrameの作成
missing_train = pd.DataFrame(train.isnull().sum())
missing_train = missing_train.rename(columns={0:'missing_value_counts'})
missing_test = pd.DataFrame(test.isnull().sum())
missing_test = missing_test.rename(columns={0:'missing_value_counts'})

fig = plt.figure(figsize=(20,20))
plt.barh(missing_train.index, missing_train.missing_value_counts, color='blue')
plt.barh(missing_test.index, missing_test.missing_value_counts, color='green')
plt.legend(['Train', 'Test'], fontsize=15)

学習用とテストデータの欠損値を重ねてプロットすることで、欠損値の傾向を確認します。
青くなっている部分が両方のデータの差を表しています。
欠損値の分布には大きな差がないようです。

#欠損値の多いカラムは削除
drop_col = ['MiscFeature', 'Fence', 'PoolQC', 'FireplaceQu', 'LotShape', 'LotFrontage', 'Alley']
train = train.drop(drop_col, axis=1)
test = test.drop(drop_col, axis=1)

学習用、テスト用それぞれのデータで同じ特徴量が多数の欠損値を持っているので削除します。
データ数が少ないので、多少の欠損値は許容範囲とします。

#ざっくりEDA

#相関係数のヒートマップ
corr_tr = train.corr()
corr_tr = pd.DataFrame(corr_tr)
sns.heatmap(corr_tr);

数値データだけですが、ヒートマップで相関係数を確認できます。

#特徴量同士の相関係数を確認※一部抜粋
corr_tr.iloc[:12, :12].style.background_gradient(cmap='coolwarm')

↑のコードでも特徴量同士の相関係数を確認できます。
特徴量同士で相関が大きい箇所もありますが、ここもデータをすべて使う方向で行きます。

high_corr = corr_tr[corr_tr['SalePrice'] > 0.6]['SalePrice']
high_corr
[out]
#材料と仕上げの質
OverallQual    0.790982
#家の広さを表すデータ
TotalBsmtSF    0.613581
1stFlrSF       0.605852
GrLivArea      0.708624
#ガレージの広さ
GarageCars     0.640409
GarageArea     0.623431
#家の値段、目的変数
SalePrice      1.000000
Name: SalePrice, dtype: float64

目的変数と高い相関を持つ特徴量を確認します。
家の値段を左右すると思われる築年数がなかったので、この時点で相関係数をあてにするのは微妙かもと思いました。
家の広さを表す特徴量ですが、フロアの違いはあるものの、根本的には家の広さを表しています。
ガレージのデータですが、収容できる車の台数と広さを表しています。これはほぼ同義だと思います。

#目的変数と特徴量に分ける
SalePrice = train["SalePrice"]
train = train.drop("SalePrice", axis=1)

#定性データの定量データのカラムリストを作る
cat_col = [col for col in train.select_dtypes(include=object)]
num_col = [col for col in train.select_dtypes(exclude=object)]

この後の処理を考え、数的データと質的データごとにリストを作りました。

定量データの特徴量を可視化して見てみます。

i = 1
plt.figure()
fig, ax = plt.subplots(9, 4, figsize=(20,15))

for feature in num_col:
    plt.subplot(9,4,i)
    sns.histplot(train[feature], color='blue', kde=True, bins=100, 
                label='train')
    sns.histplot(test[feature], color='green', kde=True, bins=100, 
                label='test')
    plt.title(feature, fontsize=8)
    plt.xlabel(' ')
    plt.legend()
    i += 1
plt.tight_layout()
plt.show();

ざっくりとですが、学習用とテスト用データともに大まかな分布の傾向は似ているようです。

同じ要領で、定性データの可視化も行います。
こっちは両方のデータで違う傾向を表す特徴量もあるようです。

目的変数SalePrice(住宅の売値)も可視化します。
sns.histplot(SalePrice, kde=True)

目的変数は右の裾が長い分布のため、外れ値の影響で平均が中央値より大きくなる分布です。
まずは外れ値を除去しない方向で進めます。

#lgihtgbm用にデータ処理

all_data = pd.concat([train, test], axis=0)

all_data[num_col] = all_data[num_col].astype('float')
all_data[cat_col] = all_data[cat_col].astype('category')

train_size = len(train)
train = all_data[:train_size]
test = all_data[train_size:]

print("train size:", train.shape)
print("test size:", test.shape)
#train size: (1460, 72)
#test size: (1459, 72)

lightgbmに適したデータ型に変更する処理をしています。
int型もfloat型にしたほうが、精度良くなりました。
後でLabeEncoderを使いやすいようにconcatしていますが、まずはデータ型の変換のみでモデルに学習させます。

#チューニングとモデル構築

ここから本題のチューニングです。

#チューニング用のモデルを作成
def objective(trial):
    params = {
        'objective':'regression',
        'metric':'r2',
        'verbosity':-1,
        'num_leaves':trial.suggest_int('num_leaves', 10, 1000),
        'max_depth':trial.suggest_int('max_depth', 8, 24),
        'learning_rate':trial.suggest_loguniform('learning_rate', 1e-8, 1.0),
        'reg_alpha':trial.suggest_loguniform('reg_alpha', 1e-5, 1.0),
        'reg_lambda':trial.suggest_loguniform('reg_lambda', 1e-5, 1.0),
        'feature_fraction':trial.suggest_uniform('feature_fraction', 0.3, 1.0),
        'bagging_fraction':trial.suggest_uniform('bagging_fraction', 0.3, 1.0),
        'bagging_freq':trial.suggest_int('bagging_freq', 1, 8),
        'min_child_samples':trial.suggest_int('min_child_samples', 5, 80),
        'random_state':8
        }
#見込みのないtrialの切り捨て
    pruning_callback = optuna.integration.LightGBMPruningCallback(trial, 'r2')
#モデルにチューニングしたパラメータを渡す
    model = lgb.LGBMRegressor(**params, n_estimators=500)
#KFold分割し、評価を行う
    kf = KFold(n_splits=4, shuffle=True, random_state=8)
    scores = cross_validate(model, X=train, y=SalePrice, scoring='r2', cv=kf)
    return scores['test_score'].mean()

Optunaに渡すためのモデルを定義しています。
ただデータ数が少ないため、元のデータをいきなりKFold分割してます。
ほんとは学習用、検証用、テスト用に分割してモデルの精度を確認したかったのですが、データ量が少ないので断念。
分かりやすくするため、あえて'regression'を明記してますが、デフォルトではこれになってます。
コンペの評価指標はRMSEですが、cross_validateで使えないので、一目で分かりやすい決定係数にしています。

モデルを作成したので、チューニングさせます。

#Optunaによるチューニング
%%time
study = optuna.create_study(direction='maximize')
study.optimize(objective, timeout=600)

#ベストなパラメーターの表示
best_params = study.best_params
print('best_params:')
[out]
best_params:
{'num_leaves': 488, 'max_depth': 12, 
'learning_rate': 0.09946325984953863, 'reg_alpha': 0.002492041819920163,
 'reg_lambda': 0.0016166727035490307, 'feature_fraction': 0.300655728931028, 
'bagging_fraction': 0.9867819626446563, 'bagging_freq': 4, 'min_child_samples': 11}

これで一番良かったtrialと最適なパラメータを確認できます。
ちなみに、study.best_trialで一番良かったtrialを確認できます。

plot_optimization_history(study)で学習の履歴を確認できますが、出力結果の画像は割愛します。
plot_param_importances(study)で学習に影響を与えているパラメータを確認したところ、圧倒的にlearning_rateが影響を与えてました。

#チューニングしたパラメータで再度学習と予測をする
#こっちは普通にKFold
%%time
sub_preds = np.zeros(test.shape[0])

kfolds = KFold(n_splits=4, shuffle=True, random_state=8)
for train_cv_no, eval_cv_no in kfolds.split(train):
    train_x_cv = train.iloc[train_cv_no]
    train_y_cv = SalePrice.iloc[train_cv_no]
    val_x_cv = train.iloc[eval_cv_no]
    val_y_cv = SalePrice.iloc[eval_cv_no]
    
    params = {
        'objective':'regression',
        'metric':'rmse',
        'verbosity':-1,
        'num_leaves':best_params['num_leaves'],
        'max_depth':best_params['max_depth'],
        'learning_rate':best_params['learning_rate'],
        'reg_alpha':best_params['reg_lambda'],
        'reg_lambda':best_params['reg_lambda'],
        'feature_fraction':best_params['feature_fraction'],
        'bagging_fraction':best_params['bagging_fraction'],
        'bagging_freq':best_params['bagging_freq'],
        'min_child_samples':best_params['min_child_samples'],
        'random_state':8   
    }

    model = lgb.LGBMRegressor(**params, n_estimators=500, early_stopping_rounds=200)
    model.fit(train_x_cv, train_y_cv, eval_set=[(val_x_cv, val_y_cv)])
    val_pred = model.predict(val_x_cv, num_iteration=model.best_iteration_)
    #submit用の予測をする。Fold数で割って平均値を算出する。
    sub_preds += model.predict(test, num_iteration=model.best_iteration_) / kfolds.n_splits
#損失関数
rmse = mse(val_y_cv, val_pred, squared=False)
print('RMSE:', rmse)

チューニングした最適なパラメータで、モデルに学習と予測を行わせます。
こっちは普通にKFoldで交差検証をします。
submit用の予測ですが、KFoldなのでn_splits分だけ大きくなります。
そのため、Fold数で割ることで平均の値を提出用の予測とします。
モデルの評価にはコンペで使われているRSMEを使います。
squared=FalseでRMSEが出力されます。

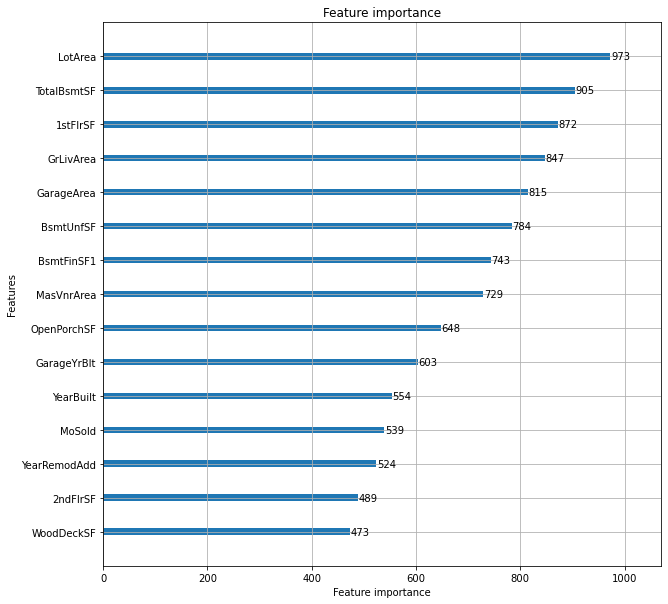
#特徴量の重要度を可視化
lgb.plot_importance(model, max_num_features=15, figsize=(10,10))
plt.show()

モデルの予測に重要だったパラメータは、最初の仮説にほぼ沿っています。
SFやAreaは広さに対するデータ、YearBuiltが家が建てられた年です。
Bsmtは地下部分のデータを意味します。
MasVnrArea(塀で囲まれているエリア、のはず)、OpenPorch(玄関ドア前の屋根下の広さ)も家が大きいほど広くなるはずなので、広さを表していると言えますね。
そこまで仮説との乖離がなかった重要度でした。
YearRemodAddは住居をリフォームした年になります。アメリカの住居事情ではリフォームすることで、資産価値が高める家主が多いようです。
築年数が重要というより綺麗に見える、手入れがされていて家の寿命が長くなる、ということの方が重要みたいです。
確かに、築年数が古くても綺麗にリフォームされていれば住みたくなりますね。

#submit用のCSVを作成
sub = pd.DataFrame({"id":test_id, "SalePrice":sub_preds})
sub.to_csv("submission.csv", index=False)

最後に、今回のコンペで指定されている形式のCSVファイルを作成してsubmitします。

#所感

submitしたスコアですが、一番良かったのが約0.124でした。
順位も変動していますが、大体上位17%あたりを彷徨ってます。

精度を上げるために試したのは、下記です。
-重要度の高い特徴量だけで学習
-相関係数の高い特徴量と築年数だけで学習
-特徴量のうち、相関の高い組み合わせがある場合は片方の削除
-PCAで定量データの次元圧縮を行う
-外れ値の除去
-数的データは列ごとの平均値、質的データは列ごとの最頻値で埋める
-LabelEncoder
-目的変数の対数化
単にデータを削る作戦は失敗でした。多重共線性の確認は割愛したので、別の機会にやろうと思います。
第三四分位数 + 1.5×IQR、つまり比較的高い価格に外れ値があったので、除去しましたが効果なし。
LabelEncoderを使って見たのですが、特に精度が良くなったりはしませんでした。
そもそも、lightgbmにカテゴリ型でデータを渡せば自動で処理してくれるので、わざわざ値を変換する必要はなさげですね。
また、int型のデータもfloat型にした方が精度が良くなりました。

結局、予測の精度上昇に貢献したのは相関の高い特徴量の削除、目的変数の対数化です。

#まとめ

今回は不動産でしたが、業務外で様々な分野のデータに触れられるのはKaggleのよさだなと思います。
業務では使わない分野のデータを扱うたびに思うのですが、データ分析にはドメイン知識が重要であることを改めて実感しました。
Kaggleで得た知見が業務に役立つこともあるので、継続していきたいです。

最後まで見てくださり、ありがとうございました。