エミリー・リール（Emily Riehl）による計算効果（モナド）の説明

はじめに

エミリー・リールの2019年の講演のスライドを見つけた。

• A categorical view of computational effects
  （Moggiの"An abstract view of programming languages"のもじり？）

計算効果のあたりの説明の紹介をしてみる（代数的効果の部分は割愛）。
ただし、valueとcomputationの説明はない。

computationの一つの構造案がモナドなので、まずvalueとcomputationがわかっていないと計算効果（もとい代数的効果も）わからないはずだが、とりあえずそこは置いておいて圏論（圏）がなんで必要なのかという部分についてだけ説明を知るのは無意味ではないはず。

話が飛んでしまった感があるので補足すると、個人的見解として、計算効果（モナド）の理解にあたっては、以下の表のように3段階ほどぐらい必要だと理解している。

段階	要点
第１層目	βη変換のみのλ計算では入出力、非決定計算、例外処理、部分性などといった効果を持つプログラムを表現できないという問題提起
第２層目	提起した問題の解決にあたって、valueとcomputationの導入、computationのvalueへの対応付け（Moggiの原理）
第３層目	圏論を用いたプログラムの圏化 　← リールの説明はこの部分

第１層目は歯が立たないが、2層目、3層目はそこまででもない（と思う）。エミリー・リールの計算効果の説明は圏論の専門家として第3層目をなぞったものだと言える。計算機科学者じゃないから第１層目、第2層目についてはそもそもコメントできないということなんだろうけれど。

あまり関係ないが、計算効果（モナド）について、圏論の専門家であるリールが、わざわざテーマを明示して説明しているというもので、圏論の勉強（圏論のモナド）をした人だったら、プログラミングのモナドについてわかっているだろうという一般的な見方は正しくないと思う。プログラミングのモナドはプログラミングのモナドで圏論と分けて知る必要がある。

リールによる説明：計算効果の圏的観点（A categorical view of computational effects）

概観

これで大体説明は完結している。

T は計算効果（computational effect）¹を意味する。計算効果の種類としては、非決定計算、例外、副作用、継続などがある。

• T-プログラムとは、型Aのvalueの集合から型BのT-computationの集合への関数² $A \overset{f}{\rightarrow} T(B)$ のことである。
  ※ 単純に「型Aから型Bへの関数」と表現していないのが気になるところだと思うが、これは 数学的関数 として取り扱いため集合論の言葉に直したいためである³。
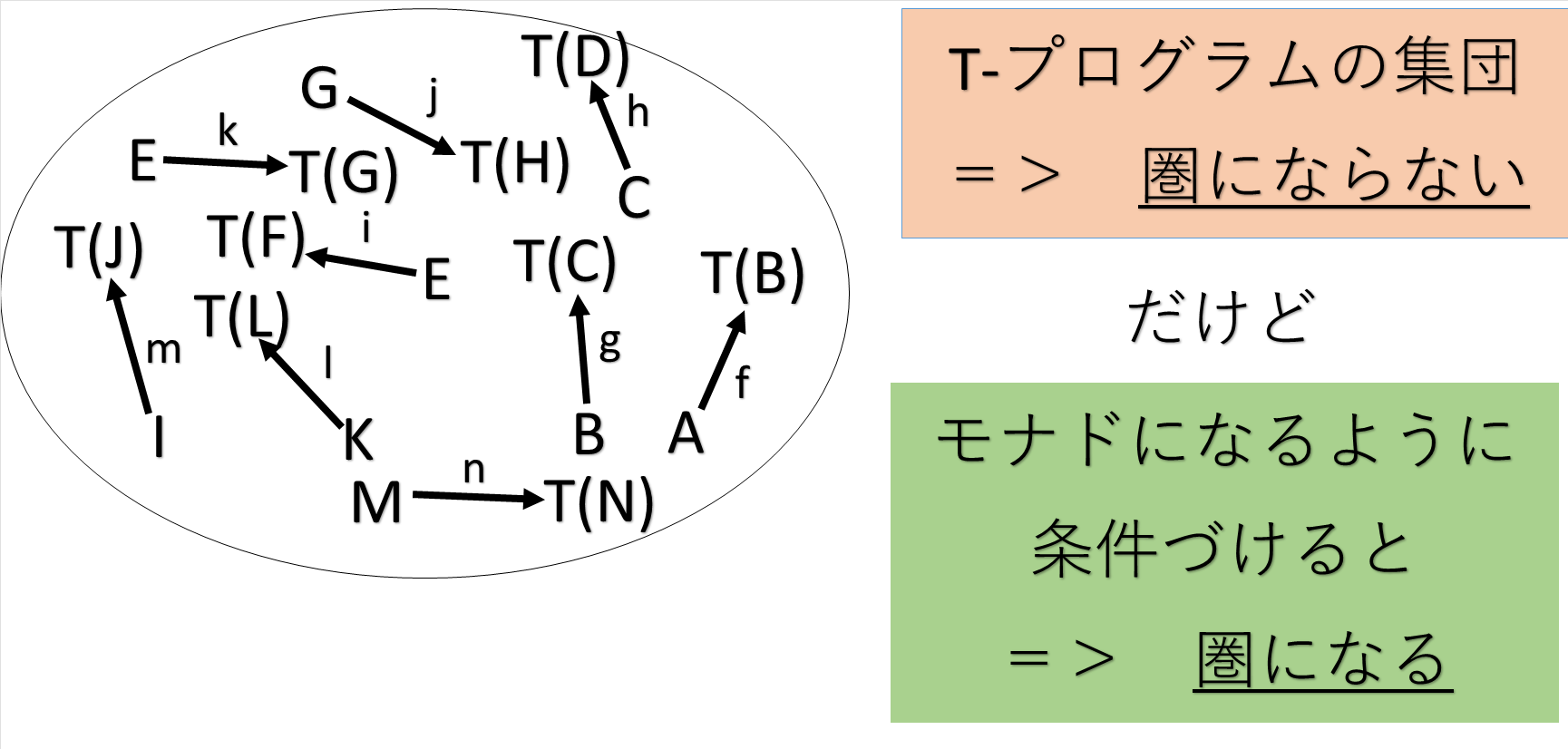
  また、型BのT-computationって何？となると思うが、ここでは天下り的に型T(B)のvalueのことだとしてもらえばいい。
• T-プログラムを圏になるようにすることを考える。ただし、ただの圏にはならない。特別な構造が必要となる。その構造が付与されるとき、Tはモナドになる。
  ※つまり、
  T-プログラムが圏を成すために必要な条件＝＝Tがモナドになる
  ということである。

時間の無い人向けまとめ

リールの言わんとするところは、ふつうの関数は素朴に合成できるので圏になるけれど、T-プログラム（たとえば、入出力付きプログラム）の集団は、素朴に合成できないので、圏にならない。だけど、モナドになるようにすると圏になる。つまり、モナドというのはT-プログラムを圏にするための条件だよ。ということを言っている。

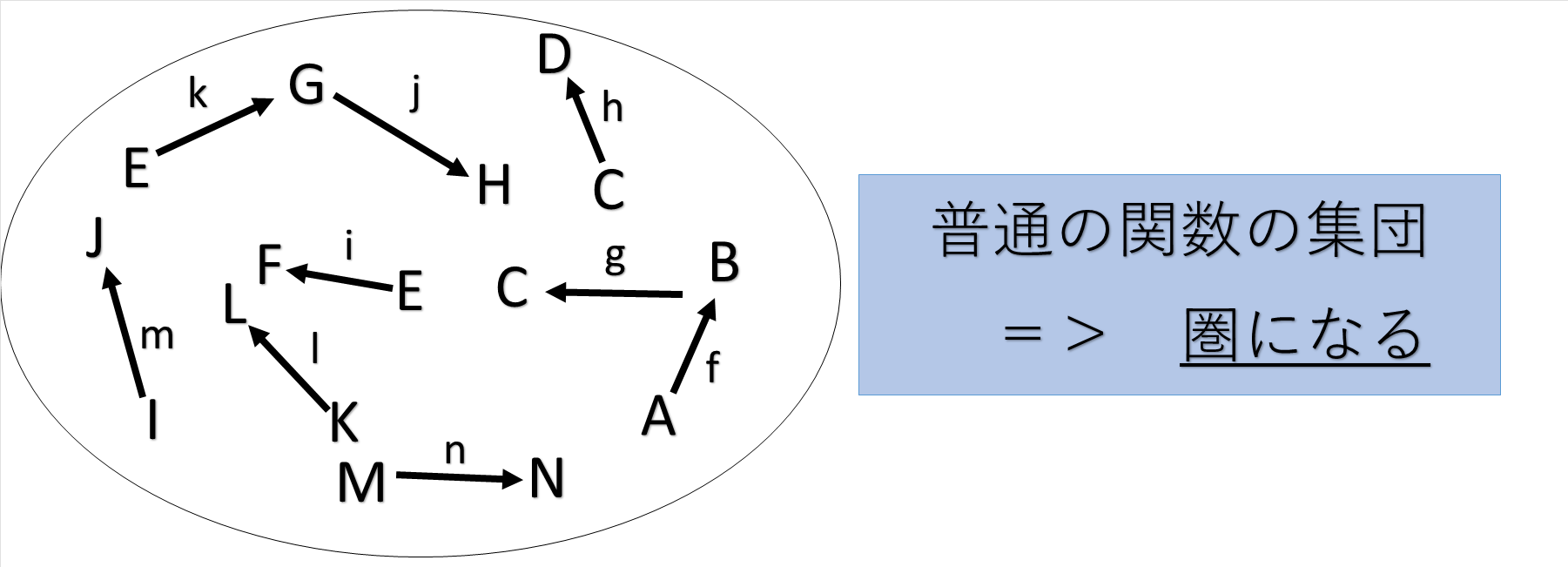
普通の関数の集団は、なにもしなくても圏になる

T-プログラムの集団は、圏にはならない。だけど、・・・。

0 関数、合成、圏（Functions, composition and categories）

数学者の観点から見た関数（function）

ここでのポイント

• リールは、プログラミングの関数を数学的関数として解釈しようとしている
• 数学的関数には必ず定義域と値域が付属する
• ある２つの関数の値域と定義域が一致さえすれば、それら関数は合成可能

圏とはなにか？

• 圏ってそもそも何？圏の定義の確認
• 圏とは対象の集団と射の集団からなり、合成射、恒等射が存在して結合律、単位元律を満たすもののことである。

恒等射のポイントは何？

• 恒等射について再確認
• 圏の構成条件は、結合律、単位元律を満たす合成射、恒等射の存在であるので、合成に加えて恒等射の存在についても強調・確認しておきたいという意図だと思われる。

具体例は省略。とりあえずSetが意味するものは集合の圏、Set圏ということが分かればいいと思う。

1 計算効果（モナド）のための圏（Categories for computational effects(monads)）

計算効果

• Set圏からSet圏への構成（自己関手）として様々な計算効果を列挙

T-プログラム

ここでのポイント

• 本筋とあまり関係ないが、Tが意味するものは、計算効果（computational effects）だったはずが、ここだけMoggiの用語計算概念（notion of computation）に表記ブレを起こしている。
• 「A から B へのT-プログラム」というものをここで定義している。数学には「プログラム（program）」なんて概念はないので定義しないといけない。そして、「A から B へのT-プログラム」とは、「型Aのvalueの集合から型BのT-computationの集合への（数学的）関数」として定義されるとしているが、Moggiの原理を説明していないので飛躍がある。
  Moggiの原理によれば、型BのT-computationは型T(B)のvalueに対応することになる。
  したがって、「A からB へのT-プログラム」とは、「型A のvalueの集合から型T(B)のvalueの集合への数学的関数」として定義されることになる。

☆【一番重要】プログラムは圏を成すはずだ

ここが計算効果の説明で一番重要なスライドである。

• リールが言いたいことは、こうである。ふつうの関数は集合の圏Setを成す。一方、T-プログラムはふつうには圏にはならない。T-プログラムは圏とはならないのであろうか？いや、
  
  プログラムは、圏を成すはずである。 とリール（とMoggi）は主張する。
• スローガンは、AからBへのT-プログラムがT-プログラムの圏の射を定義するとき計算効果 T はモナドを定義する、である。
  つまり、T-プログラム（たとえば、入出力付きプログラム）が圏を成すということと、計算効果 T（入出力IO）がモナドになるということは不可分な関係なのだということ。

T-プログラムの圏

ここでのポイント

• T-プログラムは、圏を成すはずである。この命題を満たすためには、T-プログラムについて、恒等射と合成射が存在し、しかも結合律、単位元律を満たさないといけない。
• なので、まず恒等射に相当するpure functionを導入する。
• 次は、合成射が存在することを言えばいいが、ここで大きな問題に直面する。
  
  T-プログラム同士は単純合成できないのである。というわけで、T-プログラム同士を合成させるためにbind関数というものを導入することになる（圏論的にはクライスリ合成と言う）。
• 以上から、（T,bind,pure）が定義されたT-プログラムの集団には、恒等射が存在し、しかも合成射も存在する。さらに、（T,bind,pure）の三つ組が、恒等射と合成射について、結合律、単位元律を満たせば、T-プログラムの集団は圏になり、(T,bind,pure)の三つ組はモナドになる⁴。

まとめ

モナドというと、おどろおどろしい概念のように当初聞こえたが、エミリー・リールによれば、単に計算効果ＴについてAからBへのT-プログラムが圏を成すための条件でしかない。

圏を成すとなにがうれしいかというと、モジュール性である。たとえば、計算効果Maybeのプログラムと計算効果ＩＯのプログラムがあれば、それらはそれぞれ圏をなすので、理論的に（数学的に）混じり合わない（簡単には合成できない）。

この数学的にできないという性質は、ソフトウェア工学的にできない、というのと比較して、大きな差がある（ハックの余地がないという意味で）。

今回は冒頭に書いた第1層目と第２層目に関する話を省いたが、今回のスライドの発見のように、何かの機会を見つけて記事にしたい。

脚注

1. Moggiの用語では計算概念（notion of computation）にあたると思われる。 ↩

2. ここは意外と重要で、数学者のエミリー・リールが、圏的観点から解釈すると言っている講演の中で、プログラミングにおける関数（function）をわざわざ持ち出す理由がなく、同じfunctionで紛らわしいが、ここでは数学的意味の関数について話していると解すべきである。 ↩

3. 数学的関数の定義は以下
   
   S.マックレーン『数学 -その形式と機能-』p.167 ↩

4. ちなみに、この恒等射と合成射について、結合律、単位元律を満たすに相当する条件は、プログラミングの世界ではモナド則（Monad law）と呼ばれる。 ↩