Gradient Boostingの理論を整理する

最近，いろいろなBoostingアルゴリズムを実装しています。
頭の整理も兼ねてGradient Boostingの理論を説明してみます。

Gradient Boostingとは

Gradient Boostingを一言で表現すると関数空間の勾配法です。
もう少し詳しくいうと，弱学習器集合を基底とした関数空間の座標降下法です。

これだけではよく分からないと思うので，さらに詳しく説明してみます。

勾配法

ニューラルネットワークを中心に機械学習の様々なアルゴリズムで使われています。
そして機械学習の文脈で勾配法というと，学習パラメータ空間での勾配法となると思います。

例えばニューラルネットワークなどの学習モデル$f$がパラメータ$\boldsymbol{\theta}$で表現されているとします。
さらに，最適化したい損失関数を${\cal R}(\boldsymbol{\theta})$とします。このとき，最適化問題のゴールは

$$
\hat{\boldsymbol{\theta}} = \mathrm{arg min}_{\boldsymbol{\theta}} {\cal R}(\boldsymbol{\theta})
$$

なる$\hat{\boldsymbol{\theta}}$を見つけることです。この$\hat{\boldsymbol{\theta}}$を見つけるための方法の一つが勾配法であり，

$$
\boldsymbol{\theta}^{new} \leftarrow \boldsymbol{\theta}^{old} - \eta \frac{\partial {\cal R}}{\partial \boldsymbol{\theta}}
$$

を一定回数もしくは収束するまで繰り返します($\eta$は学習率です)。

Additive model

ここで話を戻します。最初に述べた関数空間というのはどういうことでしょう。
AdaBoost，Gentle AdaBoost, XGBoostなどのBoosting手法で共通して使われている学習モデルがadditive modelです。
つまり
$$
f(\boldsymbol{x}) = \sum_{t=1}^T \alpha_t h_t(\boldsymbol{x})
$$
という形式のモデルです。この式の中の$f: {\cal X} \rightarrow \mathbb{R}$が所属している空間を${\cal F}$とします。この${\cal F}$が関数空間です。
ではこの${\cal F}$をどう表現すればよいでしょう。
上式中の$h_t : {\cal X} \rightarrow \mathbb{R}$は弱学習器であり，これを${\cal H}$の要素とします。つまり${\cal H}$は弱学習器全体の集合で，例えば決定木で表現される関数の集合がよく使われます。
実はadditive modelにおいて${\cal F}$は${\cal H}$を基底とした空間と捉えることができます。

説明を簡単にするために${\cal H}$の要素数が有限な場合を考えます。
つまり${\cal H} = \left\{h^{(1)}, h^{(2)}, \ldots, h^{(M)} \right\}$といった具合です。
このとき，${\cal F} = \left\{\boldsymbol{\beta}^{\mathrm{T}}\boldsymbol{h} | \boldsymbol{\beta} = \left(\beta^{(1)}, \beta^{(2)}, \ldots, \beta^{(M)}\right) \in \mathbb{R}^M, \boldsymbol{h} = \left(h^{(1)}, h^{(2)}, \ldots, h^{(M)}\right)\right\}$
とすると上の式のadditive modelを表現できます。
実際
$$
\boldsymbol{\beta}^{\mathrm{T}} \boldsymbol{h}(\boldsymbol{x}) = \sum_{m=1}^M \beta^{(m)} h^{(m)}(\boldsymbol{x})
$$
は上のadditive modelの式と同じ形状になっていることが確認できます。

関数空間の勾配法

関数空間の基底数が有限の場合

損失関数を${\cal R}[f]$とします。$f$がadditive modelで表現されていて${\cal H}$を関数空間の基底とします。
この考え方では$f$は関数空間${\cal F}$上の点です。関数空間で勾配法を行うということは，空間${\cal F}$で少しずつ点を動かしながら${\cal R}[f]$を小さくしていくことに他なりません。さらにいうと、関数空間の基底が有限個($M$個)の場合，$f$は$M$次元のパラメータ$\boldsymbol{\beta}$に関する勾配法になります。

つまり，$m=1, \ldots, M$に関して
$$
\beta^{(m)} \leftarrow \beta^{(m)} - \eta \frac{\partial {\cal R}}{\partial \beta^{(m)}}
$$
といった具合にパラメータ$\boldsymbol{\beta}$を更新します。
ベクトル形式で表現すると
$$
\boldsymbol{\beta} \leftarrow \boldsymbol{\beta} - \eta \frac{\partial {\cal R}}{\partial \boldsymbol{\beta}}
$$
となります。

関数空間の基底数が無限の場合

ここまで${\cal H}$の要素数を有限の値$M$としてきました。
実際には${\cal H}$は決定木で表現される関数集合といった具合に，無限の要素数を持ちます。
この場合$\partial {\cal R} / \partial \boldsymbol{\beta}$をすべて計算していくことは不可能です($\boldsymbol{\beta}$の次元が無限になっています)。
そこでGradient Boostingでは座標降下法(coordinate descent)で損失関数を最小化します。
座標降下法とは座標軸に平行な方向に限定してパラメータを更新する手法です。
関数空間の座標降下法では
1. 降下する軸(=弱学習器$h_t$)を決定する
2. 降下する幅(=$\alpha_t$)を決定する
の2つの操作を繰り返すことになります。

1. 降下する軸を決定する = 弱学習器を選択する

座標降下法では複数ある軸の中で最も負の勾配が大きい方向(=軸)を選んで降下します。
いま，Gradient Boostingにおいて座標降下を$t$回行っているとします。
このとき，$f_{t} = \sum_{s=1}^t \alpha_s h_s$です。

ここである軸$h$を選んで微小量$\epsilon \in {\cal R}$だけ進んだとします。このとき損失${\cal R}$の勾配$D{\cal R}[f_t](h)$は以下の通りです。

$$
\begin{align}
D{\cal R}[f_t](h) &= \lim_{\epsilon \rightarrow 0} \frac{{\cal R}[f_t + \epsilon h] - {\cal R}[f_t]}{\epsilon}
\end{align}
$$

さらに$N$個の訓練データを用いた経験損失${\cal R}[f_t] = 1/N \sum_{i=1}^N \phi(f_t(\boldsymbol{x}_i))$
を考えると¹

$$
\begin{align}
D{\cal R}[f_t](h) &= \lim_{\epsilon \rightarrow 0} \frac{{\cal R}[f_t + \epsilon h] - {\cal R}[f_t]}{\epsilon} \\
&= \lim_{\epsilon \rightarrow 0} \frac{\frac{1}{N} \sum_{i=1}^N \phi\left(f_t(\boldsymbol{x}_i) + \epsilon h(\boldsymbol{x}_i)\right) - \frac{1}{N} \sum_{i=1}^N \phi\left(f_t(\boldsymbol{x}_i)\right)}{\epsilon} \\
&= \lim_{\epsilon \rightarrow 0} \frac{1}{N} \sum_{i=1}^N \frac{\phi\left(f_t(\boldsymbol{x}_i) + \epsilon h(\boldsymbol{x}_i)\right) - \phi\left(f_t(\boldsymbol{x}_i)\right)}{\epsilon h(\boldsymbol{x}_i)}h(\boldsymbol{x}_i) \\
&= \frac{1}{N} \sum_{i=1}^N \phi'\left(f_t(\boldsymbol{x}_i)\right) h(\boldsymbol{x}_i)
\end{align}
$$

となります。
つまり、
$$g_t(\boldsymbol{x}) := \phi'(f_t(\boldsymbol{x})) = \left.\frac{\partial \phi(z)}{\partial z} \right|_{z = f_t(\boldsymbol{x}_i)}$$
としたとき、 $\boldsymbol{g}_t = (g_t(\boldsymbol{x}_1), g_t(\boldsymbol{x}_2), \ldots, g_t(\boldsymbol{x}_N))$ と $\boldsymbol{h} = (h(\boldsymbol{x}_1), h(\boldsymbol{x}_2), \ldots, h(\boldsymbol{x}_N)
)$の内積を使って
$$
D{\cal R}[f_t](h) = \frac{1}{N} \boldsymbol{g_t}^{\mathrm{T}} \boldsymbol{h}
$$
という表現ができます。

ここで座標降下法の話に戻ります。
座標降下法ではたくさんある軸方向の中から負の勾配が最も大きい方向を選んで降下していきます。つまり$-D{\cal R}[f](h)$が最も大きくなる$h$を選んで降下すればよいわけです。
すなわち
$$
h_{t+1} = \mathrm{argmax}_{h \in {\cal H}} (-\boldsymbol{g}_t)^{\mathrm{T}} \boldsymbol{h}
$$
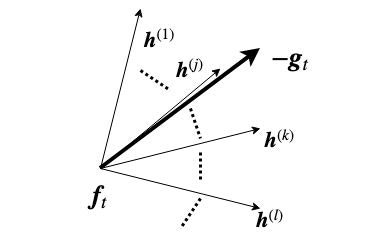
です(下図はイメージ図²)。

ところで、$h_{t+1}$は降下する方向といっていました。上の式を見ると、内積が大きくなればよいわけですが、ある$\boldsymbol{h}$に関して大きな$\gamma$をかけるとそれだけで内積は大きくなってしまいます。これを回避するために、どの$\boldsymbol{h}$もノルムは一定であるとします。
こう考えると、$-\boldsymbol{g}_t$と$\boldsymbol{h}$の内積最大化は、二乗ノルム最小化に置き換えることができます。
つまり
$$
\begin{align}
h_{t+1} &= \mathrm{argmin}_{h \in {\cal H}} \left( (-\boldsymbol{g}_t) - \boldsymbol{h}\right)^2 \\
&= \mathrm{argmin}_{h \in {\cal H}} \frac{1}{N} \sum_{i=1}^N \left(\left(-g_t(\boldsymbol{x}_i)\right) - h(\boldsymbol{x}_i)\right)^2
\end{align}
$$
です。

これは、$-g_t(\boldsymbol{x}_i), i=1, \ldots, N$に関する回帰問題を解いていることにほかなりません。このようにして弱学習器$h_{t+1}$が決定されます。

例えば${\cal H}$が回帰木の集合だとすると，$-g_t(\boldsymbol{x}_i), i=1, \ldots, N$に最もフィッティングする決定木$h$をCART法などで探索します。

2. 降下する幅を決定する

降下する方向$h_{t+1}$を決定したら，次は降下幅です。
以下の式を最小にするように降下幅$\alpha_{t+1}$を決定します。
$$
{\cal R} _t(\alpha) = {\cal R} [f_t + \alpha h_{t+1}]
$$

つまり
$$
\alpha_{t+1} = \mathrm{argmin}_{\alpha} {\cal R}_t (\alpha)
$$

です。${\cal R}_t(\alpha)$は基本的に下に凸かつ微分可能であり，line searchなどで最小化可能です。
ここのアルゴリズムは特に決まりはなく，損失関数や${\cal H}$によってはclosedな式で降下幅$\alpha_{t+1}$を決定できる場合があります(例: AdaBoost)。

まとめ

繰り返しになりますが Gradient Bootingは弱学習器の集合${\cal H}$を基底とした関数空間${\cal F}$における座標降下法です。
そして
1. 降下する方向を選択する = 負の勾配$-g(\boldsymbol{x}_i)$にフィッティングする$h \in {\cal H}$を探索する
2. 降下する幅を決定する = ${\cal R}_t(\alpha)$を最小にする$\alpha$をline search等で探索する
の2つの操作を一定回数もしくは収束するまで繰り返します。

ここまで${\cal R}$をどう定義するか, ${\cal H}$を何にするか等は決めていませんでした。
これらを決めると様々なアルゴリズムに派生していきます。
例えば，
${\cal R}[f] = 1/N \sum_i \exp(-y_i f(\boldsymbol{x}_i)) $,${\cal H} = \left\{h | h: {\cal X} \rightarrow \{-1, +1\}\right\}$とするとAdaBoostになりますし，
${\cal H}$を決定木(CART)として${\cal R}_t(\alpha)$を葉ノードごとのline searchで最適化するとMARTになります。
これ以外にもLogit BoostやXGBoost³など(粒度は違う気がしますが)様々な派生アルゴリズムがあります。

気力が残っていれば，Gradient Boostingからどのようにして種々のアルゴリズムが派生していくのか、実装はどうなるのか等もまとめるかもしれません。

---

1. $\phi: \mathbb{R} \rightarrow \mathbb{R}$です。回帰問題であれば$\phi(f(\boldsymbol{x})) = L(y, f(\boldsymbol{x})) = \left(y - f(\boldsymbol{x})\right)^2$，分類問題であれば$\phi(f(\boldsymbol{x})) = L(y, f(\boldsymbol{x})) = \exp(-yf(\boldsymbol{x}))$などをイメージしてください。 ↩

2. 基底である$h_m$の線が斜めになっているのは、①基底同士が直交している必要はないこと、②基底が無限に存在していること を伝えたい気持ちがあります ↩

3. 厳密にいうとXGBoostはGradient BoostingというよりもNewton Boostingの派生です。1次の勾配だけでなく2次の勾配も使って損失を最小化していくのがNewton Boostingです。たとえばexponential lossを使ったNewton Boostingは Gentle AdaBoostになります。 ↩