AtCoder Beginners Contest 338 (ABC338) をPythonで解きました。
見やすいコードを書く練習も兼ねてます。
A - Capitalized?
問題
文字列 $S$ が与えられます。 $S$ の先頭1文字が英大文字でそれ以外が英小文字のときYesを、そうでないときNoを出力してください。
考察
for文で各文字が条件を満たしているかどうかを判定していきます。
アルファベットは全部で $26$ 文字しかなく、これくらいなら全列挙してもいいでしょう。
つまり、最初にuppercase = "ABCDEFGHIJKLMNOPQRSTUVWXYZ" と気合いで英大文字を全列挙しておき、「ある文字がこのuppercaseの中に含まれていればそれは英大文字、そうでなければ英小文字」と判定します。
コード
uppercase = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
S = input()
N = len(S)
for i in range(N):
if i == 0:
if S[i] not in uppercase:
print("No")
exit()
else:
if S[i] in uppercase:
print("No")
exit()
print("Yes")
別解
string.ascii_uppercaseをつかった解法
uppercase = "ABCDEFGHIJKLMNOPQRSTUVWXYZ" と書く部分について、これは下のコードと同じです。
import string
uppercase = string.ascii_uppercase # "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
VSCodeやPyCharmなどのエディタにはコードを予測して補完してくれる機能があるので、この方法だとコード量も減りますし、間違って1文字だけ抜かしてしまうようなヒューマンエラーも起きません。
import string
uppercase = string.ascii_uppercase # "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
S = input()
N = len(S)
for i in range(N):
if i == 0:
if S[i] not in uppercase:
print("No")
exit()
else:
if S[i] in uppercase:
print("No")
exit()
print("Yes")
.isupper()をつかった解法
.isupper()をつかうと、英大文字かどうかを判定することができます。
英小文字の場合は.islower() です。
""".isupper()の使用例"""
S = "AtCoder"
for s in S:
if s.isupper():
print("upper")
elif s.islower():
print("lower")
# 出力結果
# upper
# lower
# upper
# lower
# lower
# lower
# lower
これをつかうと、英大文字・英小文字の判定を簡潔に記述できます。
S = input()
for i in range(len(S)):
if i == 0:
if S[i].islower():
print("No")
exit()
else:
if S[i].isupper():
print("No")
exit()
print("Yes")
.istitle()をつかった解法
先頭1文字が英大文字でそれ以外が英小文字であればTrueを返し、そうでなければFalseを返すメソッド.istitle() をつかいます。
S = input()
if S.istitle():
print("Yes")
else:
print("No")
B - Frequency
問題
文字列 $S$ が入力で与えられます。文字列 $S$ に含まれる文字の中で、最も多く登場するのは何ですか?複数ある場合は、アルファベット順で最もはやいもののみを答えてください。
考察
まず、どの文字が何回登場しているのかを数えます。
今回は辞書dictをつかって管理してみます(別解に他の方法も載せています)。
コードにするとこんな感じ。
"""どの文字が何回登場しているかを管理する辞書をつくる"""
S = input()
dic = dict()
for alp in S:
if alp not in dic:
dic[alp] = 0
dic[alp] += 1
次に、変数を2つ用意します。答えとなる文字を表す ans と、その文字の登場回数を表す max_cnt です。
辞書内の要素を1つずつ見ていき、その中で
- $\text{max_cnt} \lt (要素の登場回数)$
- $\text{max_cnt} = (要素の登場回数)$ かつ アルファベット順で $ans$ よりもはやい。
のどちらかを満たしていれば ans と max_cnt を更新します。
全体のコードは下のようになります。
コード
S = input()
dic = dict()
for alp in S:
if alp not in dic:
dic[alp] = 0
dic[alp] += 1
ans, max_cnt = 'a', 0
for alp, alp_cnt in dic.items():
if (max_cnt < alp_cnt) or (max_cnt == alp_cnt and alp < ans):
ans, max_cnt = alp, alp_cnt
print(ans)
辞書にcollections.defaultdictをつかう解法
defaultdictをつかえば、存在していないキーにアクセスしてもKeyErrorを起こさずにその値を $0$ として扱うことができます。from collections import defaultdict
S = input()
dic = defaultdict(int)
for alp in S:
dic[alp] += 1
ans, max_cnt = 'a', 0
for alp, alp_cnt in dic.items():
if (max_cnt < alp_cnt) or (max_cnt == alp_cnt and alp < ans):
ans, max_cnt = alp, alp_cnt
print(ans)
collections.Counterをつかう解法
collections.Counterをつかうと、簡単に要素の個数を数えられます。
from collections import Counter
S = input()
C = Counter(S)
ans, max_cnt = 'a', 0
for alp, alp_cnt in C.items():
if (max_cnt < alp_cnt) or (max_cnt == alp_cnt and alp < ans):
ans, max_cnt = alp, alp_cnt
print(ans)
C - Leftover Recipes
問題
$i=1, 2, \cdots ,N$ について、材料 $i$ は $Q_i$ グラムあります。
料理Aをつくるのに、材料 $i$ が $A_i$ グラム必要です。
料理Bをつくるのに、材料 $i$ が $B_i$ グラム必要です。
最大でいくつの料理が作れますか?
考察1: 全探索をする
まず思いつくのは、料理A, Bの個数を全探索してみることです。つまり、$\text{(料理Aの個数, 料理Bの個数)}$ のペアとしてありえるものをすべて列挙し、材料の量が足りているかどうかを確認します。
しかし、制約が $Q_i \leq 10^6$ なので、料理A, B の個数はどちらも最大で $10^6$ 個つくることができ、$\text{(料理Aの個数, 料理Bの個数)}$ のペアとしてありえるものは $10^{12}$ 個くらいになってしまいます。
AtCoderでは問題の実行時間制限はたいてい $2$ 秒で、$2$ 秒の間にできる計算は多くても $10^8$ 回程度です(Pythonは遅い言語なので、これも厳しいくらいです)。
なので、料理A, Bの個数を全探索する方針は、実行時間制限をオーバーしてしまいます。
考察2: 料理Aの個数のみを全探索する
料理Aの個数が $x$ 個のとき、$i=1, 2, \cdots ,N$ について材料 $i$ は $A_i \times x$ グラムだけつかいます。
すると、材料 $i$ の残りは $Q_i - (A_i \times x)$ グラムです。
この状況で、料理Bをどれだけ作れるかを考えます。
$i=1, 2, \cdots ,N$ について、料理Bを1つつくるのに材料 $i$ は $B_i$ グラムだけ必要で、いま材料 $i$ は $Q_i-(A_i \times x)$ グラムだけあるので、材料 $i$ だけを見れば料理Bは $\{Q_i-(A_i \times x)\} / B_i$ 個だけつくれます(小数点以下は切り捨て)。
$i=1, 2, \cdots ,N$ について、 $\{Q_i-(A_i \times x)\} / B_i$ (小数点以下は切り捨て) の値を計算し、その最小値が料理Bの最大の個数になります。
材料の種類数 $N$ の制約は $N \leq 10$ で、料理Aの個数は最大でも $10^6$ 個なので、最悪でも $10^7$ 回程度の計算で済みます。
これで実行制限時間 $2$ 秒におさめることができました。
コード
N = int(input())
Q = list(map(int, input().split()))
A = list(map(int, input().split()))
B = list(map(int, input().split()))
ans = 0
for x in range(10 ** 6 + 1):
leftover = [Q[i] - A[i] * x for i in range(N)] # 料理Aをx個だけつくったときの各材料の余り
if min(leftover) < 0:
break
y = 999999999
for i in range(N):
if B[i] > 0:
y = min(y, leftover[i] // B[i])
ans = max(ans, x + y)
print(ans)
D - Island Tour
問題
島が環状に $N$ 個並んでいます。隣り合った島にのみ橋がかけられていて、橋を通ってでしか移動はできません。
島 $X_1$ からスタートして島 $X_2, X_3, \cdots ,X_M$ と移動したいです。
ただしどこかの橋を1つ封鎖します。封鎖する橋を自由に選べるとき、このツアーの最短移動距離を求めてください。
考察1: シミュレーションする
ある島から別の島へ移動するとき、時計回りか反時計回りの2択しかありません。
また、どこかの橋が1つ封鎖されたとき、その2択のうち1つはできなくなり、残った1通りのルートにしか進めません。
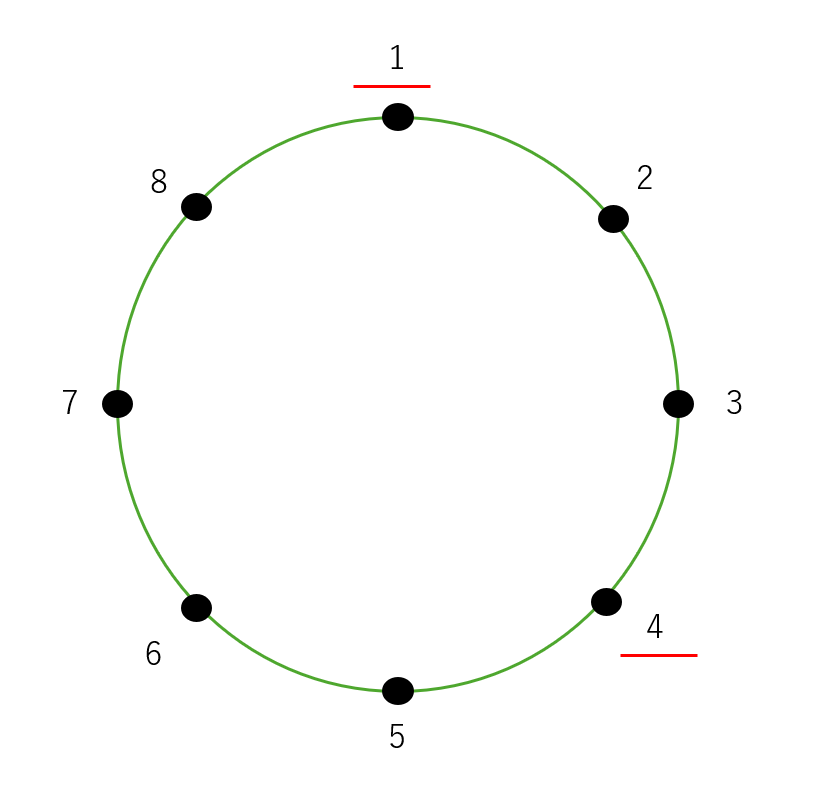
これを踏まえたうえで、島の数 $N=8$ で、島 $1$ から島 $4$ へ移動することを考えてみます。
- 島 $2$ と島 $3$ の間が封鎖されたとき
- このとき、時計回りの道は封鎖されているので反時計回りに移動するしかありません。この距離は $1-4+N=1-4+8=5$ です。
- 島 $5$ と島 $6$ の間が封鎖されたとき
- このとき、反時計回りの道は封鎖されているので時計回りに移動するしかありません。この距離は $4-1=3$ です。
これを $M-1$ 回の移動・ $N$ 個の橋に対して行うと、次のようなコードになります。
"""考察1までのコード"""
N, M = map(int, input().split())
X = list(map(lambda x: int(x) - 1, input().split()))
# dist[x]: 島xから島x+1の間の橋が封鎖されたときの総移動距離
dist = [0] * N
for i in range(M - 1):
a, b = X[i], X[i + 1]
# 島aから島bへの移動距離だけを見ているので、a<bとなるように変数を入れかえても問題ない
if a > b:
a, b = b, a
for x in range(N):
if a <= x < b:
dist[x] += a - b + N # 反時計回りルートを通る
else:
dist[x] += b - a # 時計回りルートを通る
ans = min(dist)
print(ans)
しかしこのコードの計算量は $O(MN)$ で、制約は $M,N \leq 2\times 10^5$ なので実行時間制限に間に合いません。
考察2: いもす法をつかう
だいたい同じような処理をしているところは、計算量を改善する余地があることが多いです。
考察1のコードだと、for文で $N$ 回ループしている下の部分が該当します。
for x in range(N):
if a <= x < b:
dist[x] += a - b + N # 反時計回りルートを通る
else:
dist[x] += b - a # 時計回りルートを通る
区間に対して何か数字を足したり引いたりするとき、またそれが区間や数字を変えて何度も行われるとき、いもす法がつかえます。
いもす法をつかうと、下の解答コードになります。
コード
N, M = map(int, input().split())
X = list(map(lambda x: int(x) - 1, input().split()))
# dist[x]: 島xから島x+1の間の橋が封鎖されたときの総移動距離
dist = [0] * N
for i in range(M - 1):
a, b = X[i], X[i + 1]
# 島aから島bへの移動距離だけを見ているので、a<bとなるように変数を入れかえても問題ない
if a > b:
a, b = b, a
# [a, b) の区間にd1=a-b+Nをプラスする
d1 = a - b + N
dist[a] += d1
dist[b] -= d1
# [b,N), [0,a) の区間にd2=b-aをプラスする
d2 = b - a
dist[b] += d2
dist[0] += d2
dist[a] -= d2
for i in range(N - 1):
dist[i + 1] += dist[i]
ans = min(dist)
print(ans)
E - Chords
問題
円周上に $2N$ 個の点が等間隔にあって、 $i=1, 2, \cdots ,N$ について弦 $i$ は点 $A_i, B_i$ を結んでいます。交差している弦があるならYesを、そうでないなら Noを出力してください。
考察
重要な事実として、弦 $i$ と弦 $j$ が交差しているとき、$A_i$ と $B_i$ の間に弦 $j$ の端点が1つだけ存在しています。
以下、 $A_i \lt B_i$ とします。入力で $A_i \gt B_i$ だった場合は $A_i, \enspace B_i$ を入れかえることにします。
長さ $2N$ のリスト $chord$ をつくります。$i=1, 2, \cdots ,N$ について $chord[A_i]=1, \enspace chord[B_i]=-1$ とします。
こうすると、$i=1, 2, \cdots ,N$ について、 開区間 $(A_i, B_i)$ での$chord$ の値の総和が $1$ 以上のとき、$A_i$ と $B_i$ の間に端点が1つしか含まれていない弦がある(=弦 $i$ と交差している弦が存在する)ことになります。
区間の値の総和を求めるときはFenwick Treeが便利です。下の解答コードではac-library-pythonのものをインポートしてつかっています。
コード
from atcoder.fenwicktree import FenwickTree
N = int(input())
ft = FenwickTree(N * 2)
chord = []
for _ in range(N):
a, b = map(lambda x: int(x) - 1, input().split())
if a > b:
a, b = b, a
ft.add(a, 1)
ft.add(b, -1)
chord.append((a, b))
for a, b in chord:
if ft.sum(a + 1, b) > 0:
print("Yes")
exit()
print("No")