AtCoder Beginners Contest 339 (ABC339) をPythonで解きました。
見やすいコードを書く練習も兼ねてます。
A - TLD
問題
文字列 $S$ を . で分割したとき、末尾の文字列を出力してください。
考察
文字列 $S$ を後ろ(右側)から順番に見ていきます。
. を見つけたら、そこから末尾までの文字列を出力し、for文をbreakで打ち切っておしまいです。
↓ 下のコードの解読でつまづきそうなところを折りたたみにしてあります。
for文をいつもと逆順にまわすreversed()
reversed() をつけると、逆順にfor文を回せます。
# 普通のfor文
array = []
for i in range(1, 6):
array.append(i)
print(array) # [1, 2, 3, 4, 5]
# reversedをつかうとこうなります。
array = []
for i in reversed(range(1, 6)):
array.append(i)
print(array) # [5, 4, 3, 2, 1]
末尾までの文字列を取得する方法
S[x:] とすると、(左端を0番目として) $x$ 番目から末尾までの文字列を取得できます。
"""使用例"""
S = "AtCoder"
print(S[3:]) # oder
print(S[1:]) # tCoder
print(S[5:]) # er
コード
S = input()
length = len(S)
for i in reversed(range(length)):
if S[i] == '.':
print(S[i + 1:])
break
別解
split()をつかった解法
競プロの入力受け取りでよくつかっている `.split()` は、引数に何も指定していないと、半角スペース区切りで文字列を分割してくれていました。 今回は、半角スペース区切りではなく `"."` の文字で区切りたいので、引数にこの文字を入れるとうまく `"."` で区切ってくれます。S = list(input().split("."))
ans = S[-1]
print(ans)
B - Langton's Takahashi
問題
グリッド上の高橋くんは、今いるマスが白なら黒に、黒なら白に塗り替えます。
黒に塗ったなら時計回り、白に塗ったなら反時計回りの向きで $90$ 度だけ回転し、1マス進みます。
上の行動を $N$ 回した後のグリッドを出力してください。
考察
時計回りや反時計回りに動くとき、先に向きをまとめたリストを作っておきましょう。
今回はインデックスを $1$ つ増やすと時計回りに、$1$ つ減らすと反時計回りに $90$ 度回転するような順番で書いています。
Vec = [
(-1, 0), # 上
(0, 1), # 右
(1, 0), # 下
(0, -1) # 左
]
あとは問題文に書いてある通りに実装します。
下のコードでは、高橋くんのi座標、j座標、向き(リストVecでのインデックス)の $3$ つを管理しながらシミュレーションしています。
実装の際は下のことに気をつけてください。
- 高橋くんの向き $v$ について、時計回りに $90$ 度回転するとき基本的には $v$ を $1$ だけ増やせばいいですが、左向き( $v=3$ )から回転すると上向き( $v=0$ ) になります。下の実装では、$4$ で割ったあまりを求めることでこれを解決しています。反時計回りのときも同様に気をつけてください
- 高橋くんのいるグリッドはトーラス上で、上下・左右がつながっています。下の実装では、i座標は $H$ で、j座標は $W$ で割ったあまりを求めることで解決しています
コード
Vec = [
(-1, 0), # 上
(0, 1), # 右
(1, 0), # 下
(0, -1) # 左
]
H, W, N = map(int, input().split())
Grid = [['.'] * W for _ in range(H)]
i, j, v = 0, 0, 0 # 高橋くんのi座標, j座標, 向き(Vecでのインデックス)
for _ in range(N):
if Grid[i][j] == '.':
Grid[i][j] = '#'
v = (v + 1) % 4
else:
Grid[i][j] = "."
v = (v - 1) % 4
di, dj = Vec[v]
i, j = (i + di) % H, (j + dj) % W
for row in Grid:
print(*row, sep='')
C - Perfect Bus
問題
はじめバスには $0$ 人以上の乗客が乗っていて、$i$ 番目の停車駅で乗客は $A_i$ 人だけ増えました( $A_i$ が負のときもあります)。
与えられた情報に矛盾しない現在のバスの乗客の数として考えられる最小値を求めてください。
考察1: シミュレーションする
バスの乗客が負の数になってはいけません。
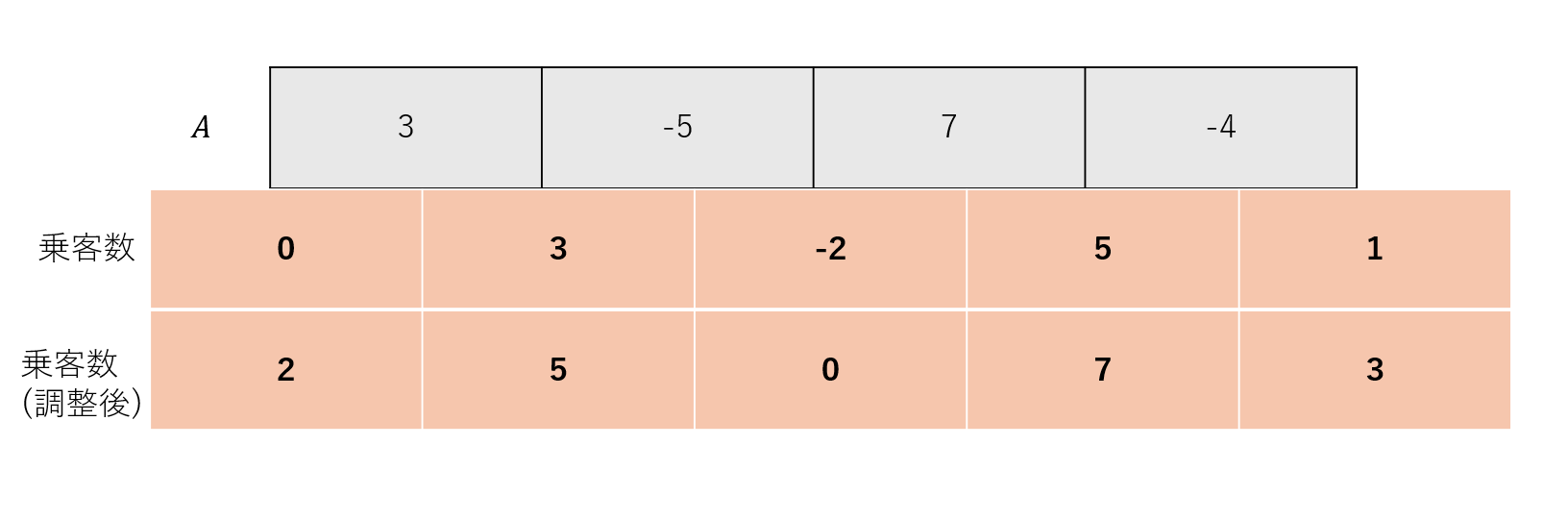
ですが、そのルールはいったん無視して、最初のバスの人数が $0$ 人だったときの乗客人数の推移を見てみます。
サンプル1の入力では、 $A=(3, -5, 7, -4)$ でした。
乗客数が負の数になってはいけないはずでした。
なので、乗客数の推移の中で出てきた最小値、今回は $-2$ を $0$ にするため、全体に $2$ をプラスします。
言い換えると、最初バスに $2$ 人が乗っていたことにすると、乗客数は常に $0$ 以上でうまくいきます。
最終的に乗客数は $3$ 人になっており、これが答えになります。
考察2: 解く
リスト $A$ をもとに乗客数の推移をつくったところは、競プロ風に言うと「累積和」です。
累積和は、itertools.accumulate() が便利です。
from itertools import accumulate
N = int(input())
A = list(map(int, input().split()))
acc = [0] + list(accumulate(A)) # 乗客数の推移(調整前)
その後、この累積和リストに出てくる最小値を $0$ にするような数を全体に足したのでした。
リスト内の最小値は min() をつかえます。
実際にリスト $acc$ の各要素に足し算していってもいいですが、今回は最後の乗客数だけが重要なので、コードはこうなります。
acc = [0] + list(accumulate(A)) # 乗客数の推移(調整前)
ans = acc[-1] + min(acc)
print(ans)
まとめると、下のコードになります。
コード
from itertools import accumulate
N = int(input())
A = list(map(int, input().split()))
acc = [0] + list(accumulate(A))
ans = acc[-1] - min(acc)
print(ans)
D - Synchronized Players
問題
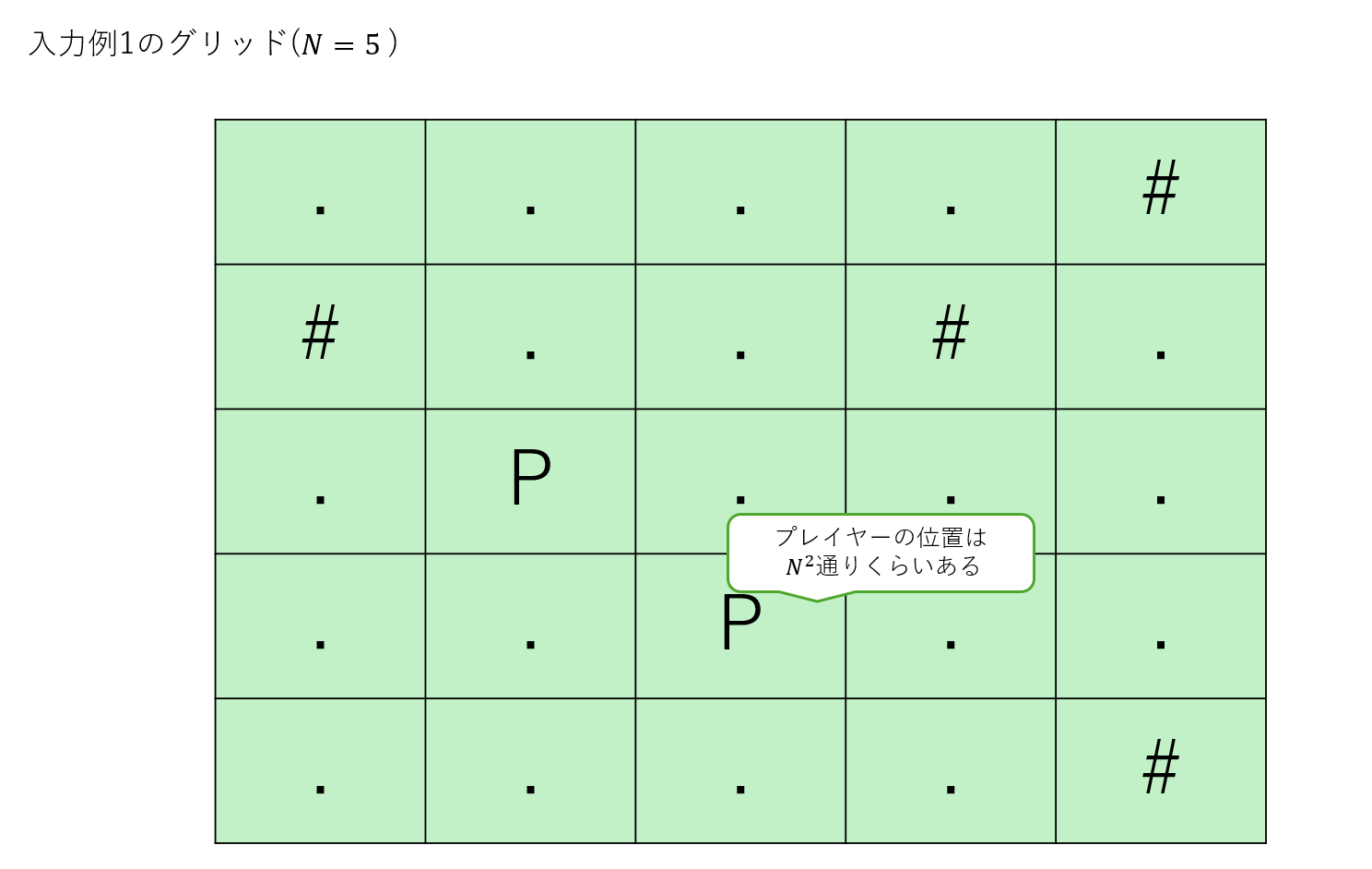
$N$ 行 $N$ 列のグリッド上に $2$ 人のプレイヤーがいます。
「この $2$ 人のプレイヤーを同時に上下左右いずれかの方向に $1$ マスだけ移動させる(ただし範囲外に出たり障害物があって進めない場合、そのプレイヤーは移動しない)」を $1$ 回の操作とします。
$2$ 人のプレイヤーの座標が等しくなるために必要な操作回数の最小値は?
考察1: 取れる状態の数を考える
取れる状態の数がいくつあるかを考えてみます(この考え方はよく競プロに出てきます)。
今回の問題では、グリッド上で変化するのはプレイヤー $2$ 人の座標だけです。
なので、 $\text{(プレイヤー1の座標, プレイヤー2の座標)}$ が最大で何パターンあるのかを数えます。
グリッドのマスは全体で $N^2$ 個あります。
各プレイヤーの取りうる座標が $N^2$ 通りくらいあるので、$\text{(プレイヤー1の座標, プレイヤー2の座標)}$ は全体で $N^4$ 通りくらいあります。
今回の問題では $N \leq 60$ なので、$N^4 \leq 60^4 = 12960000 \leq 1.3 \times 10^7$ です。
Pythonだと実行時間が $2$ 秒以内におさまるかギリギリのラインですが、
- 今回の問題では実行時間制限が普段と違って $4$ 秒になっている
- 実は $2$ 人のプレイヤーは区別する必要がなく、取れる状態の数はざっくり見積もって半分くらいに抑えられる
の $2$ 点から、実行時間制限には間に合いそうです。
考察2: 実装を工夫する
ここまで分かれば、あとは幅優先探索BFSをつかって、すべての状態についてその状態にするまでの操作回数の最小値を求めればいいです。
あとは実装すればいいですが、何も工夫せずに書くとそこそこコード量があり、また前述の通りちょっと実行時間制限をオーバーしてTLEになる危険があります。
考察2-1: 配列の次元を落とす
$dp[i_1][j_1][i_2][j_2]$ : プレイヤー $2$ 人の座標が $(i1, j1), (i2, j2)$ となるまでの最小操作回数
として実装すると、他の部分の実装を工夫していない限り、実行時間制限がそこそこきつくなりそうです。
提出コード(TLE)
Pythonは実行が遅い言語なので、工夫が必要です。
$pos_{i,j} = i \times N + j$ として、プレイヤーの座標を1変数で表すと、先ほどのdpは、
$dp[pos_{i_1, j_1}][pos_{i_2, j_2}]$ : プレイヤー $2$ 人の座標が $(i1, j1), (i2, j2)$ となるまでの最小操作回数
と書けます。
計算回数自体は変わらないですが、配列の次元を落とすと実行速度がはやくなります。
ここまでのコードはこんな感じ。
"""考察2-1までのコード"""
from collections import deque
def pos(i, j):
return i * N + j
N = int(input())
S = [input() for _ in range(N)]
P = [] # プレイヤーの座標を格納する
for i in range(N):
for j in range(N):
if S[i][j] == 'P':
P.append(pos(i, j))
# dp[pos1][pos2]: プレイヤー2人の座標がpos1, pos2となるまでの最小操作回数
dp = [[-1] * (N * N) for _ in range(N * N)]
p1, p2 = P
dp[p1][p2] = dp[p2][p1] = 0
que = deque()
que.append((p1, p2))
while que:
# ここから幅優先探索BFSの実装をする
pass
考察2-2: 実装を簡潔にする
幅優先探索BFSの部分の実装をしてみると、思っているよりもコード量が多いです。
BFSをしているwhile文の中で長いコードを書くのはしんどいので、こういうのは関数に分けてしまいましょう。
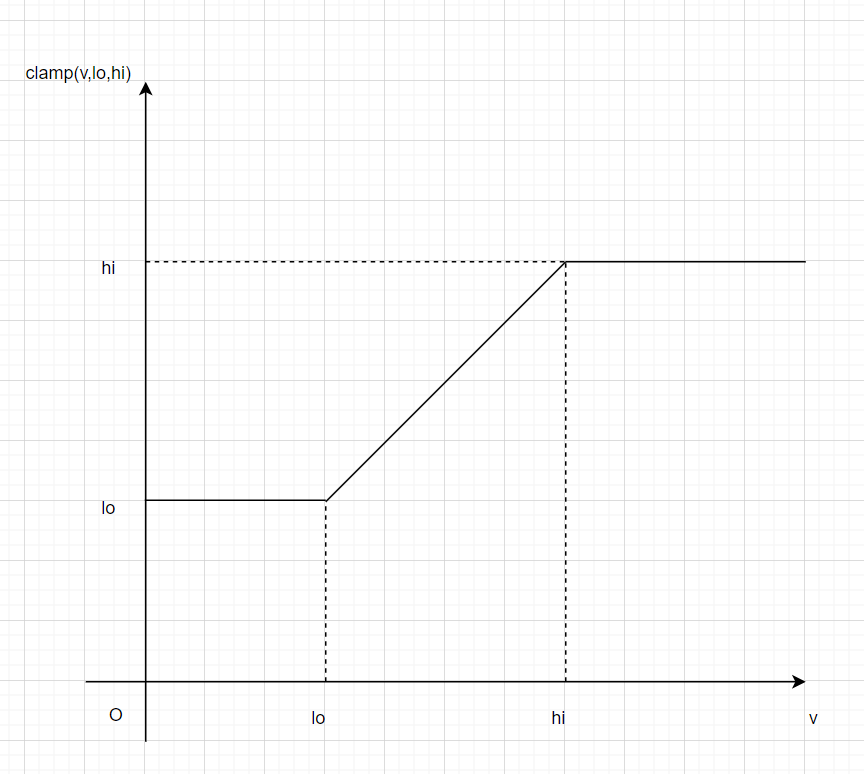
下のコードでは、clamp関数とよばれる関数を入れています。
グラフにするとこんな感じ。
グリッドの範囲外に出るような移動はできないルールで、範囲外に移動しないようにするため導入しています。
コード
from collections import deque
Vec = [(1, 0), (-1, 0), (0, 1), (0, -1)]
INF = 1 << 63
def pos(i, j):
return i * N + j
def clamp(v, lo, hi):
if v < lo:
return lo
if hi < v:
return hi
else:
return v
def moved_pos(position, di, dj):
i, j = divmod(position, N) # positionをNで割ったときの、商と余りを計算する関数divmod
nex_i, nex_j = clamp(i + di, 0, N - 1), clamp(j + dj, 0, N - 1)
if S[nex_i][nex_j] == '#':
return position
else:
return pos(nex_i, nex_j)
N = int(input())
S = [input() for _ in range(N)]
P = [] # プレイヤーの座標を格納する
for i in range(N):
for j in range(N):
if S[i][j] == 'P':
P.append(pos(i, j))
# dp[pos1][pos2]: プレイヤー2人の座標がpos1, pos2となるまでの最小操作回数
dp = [[-1] * (N * N) for _ in range(N * N)]
p1, p2 = P
dp[p1][p2] = dp[p2][p1] = 0
que = deque()
que.append((p1, p2))
while que:
p1, p2 = que.popleft()
for di, dj in Vec:
nex_p1, nex_p2 = moved_pos(p1, di, dj), moved_pos(p2, di, dj)
if dp[nex_p1][nex_p2] == -1:
dp[nex_p1][nex_p2] = dp[nex_p2][nex_p1] = dp[p1][p2] + 1
que.append((nex_p1, nex_p2))
ans = INF
for p in range(N * N):
if dp[p][p] != -1:
ans = min(ans, dp[p][p])
if ans == INF:
print(-1)
else:
print(ans)
E - Smooth Subsequence
問題
数列 $A$ の部分列(連続でなくてもok)で、どの隣接 $2$ 項間も差の絶対値が $D$ 以下になるようなものの長さの最大値はいくつですか?
考察
動的計画法DPっぽく考えて解きます。
$$dp[v] = \text{数列Aの部分列で、末尾の値が $v$ になるものの長さの最大値}$$
として、このリスト $dp$ を $A_1$ から順に見ていって更新していきます。
もらうDPの要領で考えると、数列 $A$ の第 $i$ 項 $A_i$ について見て $dp$ を更新するとき、$v=A_i-D, A_i-D+1, \cdots , A_i+D$ について、$dp[v]$ の値の最大値を取得しないといけません。
区間の最大値を求めるといえば、セグメントツリーです。
このdp配列をそのままセグメントツリーに変更することで、$dp[v]$ の値の最大値を取得するのに $O(\log N)$ かかり、全体として $O(N \log N)$ でこの問題を解くことができます。
コード
from atcoder.segtree import SegTree
Ma = 500_000
INF = 1 << 63
def segment(v):
return max(v - D, 0), min(v + D, Ma)
N, D = map(int, input().split())
A = list(map(int, input().split()))
dp = SegTree(max, -INF, Ma + 3)
for a in A:
l, r = segment(a)
result = max(1, dp.prod(l, r + 1) + 1)
dp.set(a, result)
ans = dp.all_prod()
print(ans)