はじめに
ふと美しい数式をプロットしたくなり、美しい数式を眺めていたら、綺麗なハート型になる数式を見つけた。
その数式をPythonでプロットしてみることにした。
なんとなくスマホですっとハートを出せるようにしたくなったため、Pythonistaで動作するように作成した。
実装方針
元となる数式について
描きたい数式:
$$(x^2 + y^2 - 1)^3 = x^2 y^3$$
これを$y$について解くと
$$y = \frac{1}{2}(x^\frac{2}{3} \pm \sqrt{x^\frac{4}{3} + 4 (1 - x^2)})$$
実数の平方根は正であるから、$x^\frac{4}{3} + 4 (1 - x^2) \ge 0$である。
これを解くと
$$-1.1390 \lessapprox x \lessapprox 1.1390$$
問題:Pythonistaで立方根を求めるnumpy.cbrtが使えない!
numpy.cbrtがimportできない場合に、cbrtの代わりとなるものを作りたい。
powで立方根自体は求められるが、引数が負数になるとエラーとなってしまう。
つまり、$x$が正($x\ge0$)のとき
pow(x, 1/3)
を返したい。また、$x$が負($x<0$)のとき
-pow(-x, 1/3)
を返したい。
numpy.ndarrayでは、x[条件式]で条件式を満たすものを抽出することができる。
すなわち、$x\ge0$のものを抽出する場合は以下のようになる。
x[x >= 0]
以上のことをまとめると、cbrtは以下のように書くことができる。
cbrt = lambda x: np.append(-pow(-x[x < 0], 1/3), pow(x[x >= 0], 1/3))
コード
"""ハート型をプロットする"""
import matplotlib.pyplot as plt
import numpy as np
# Pythonistaのnumpyではcbrtが使えないため
try:
from numpy import cbrt
except ImportError:
cbrt = lambda x: np.append(-pow(-x[x < 0], 1/3), pow(x[x >= 0], 1/3))
def numpy_heart():
"""ハート型をプロットする
数式:(x^2 + y^2 - 1)^3 = x^2 * y^3
yについて解いた数式:y = 1/2 * (x^(2/3) +- sqrt(x^(4/3) + 4 * (1 - x^2)))
実数の平方根は正であるから、
x^(4/3) + 4 * (1 - x^2) = 0の解が, x ~ +-1.1390であるため、
xが+-1.1390の範囲を計算し、プロットする。
"""
x = np.arange(-1.1390, 1.1391, 0.0001)
y_sqrt = np.sqrt(x * cbrt(x) + 4 * (1 - np.power(x, 2)))
y_positive = (np.power(cbrt(x), 2) + y_sqrt) / 2
y_negative = (np.power(cbrt(x), 2) - y_sqrt) / 2
plt.plot(x, y_positive, color="pink")
plt.plot(x, y_negative, color="pink")
plt.show()
def main():
numpy_heart()
if __name__ == '__main__':
main()
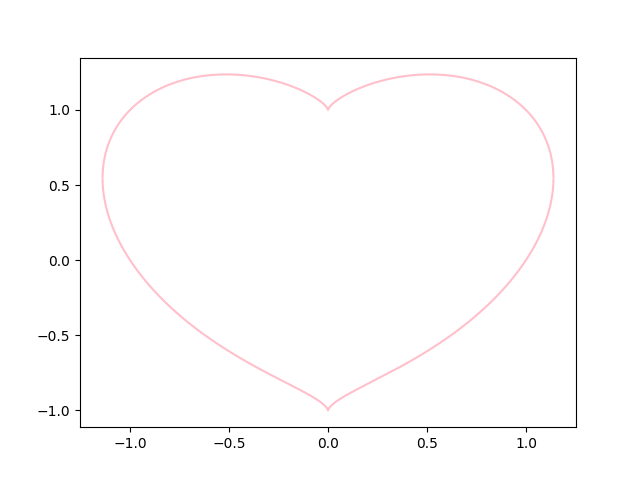
実行結果
実行結果のハート型のプロット画像