再帰関数について調べてみると
「より簡単に、より直感的に複雑な処理ができる」と書いている記事が多く見受けられました。
その通り確かにループ処理などより、少ないコード数で複雑な処理を書けたりするのですが
おバカな僕には再帰処理それその物がトリッキーな作りに感じられ、感覚的にしっくり来なかった上に
ツリー構造のような複雑なものに再帰関数を適用したもの、となると理解するのに結構苦労したんで
自分の考えを整理するためにも、ツリー構造で使用する再帰関数についてまとめたものを書いてみました。
言語はCです。
再帰関数とは?
関数の処理の中で、自分自身を呼び出している関数のことです。
例
void func(){
func();
}
こんな感じの関数のことです。
ルール
再帰関数を使用する時は、必ず守らなければならない以下の2つの単純なルールがあります。
1. 呼び出す度に、関数の処理をより単純化させなければならない。
2. 必ず終点がなければない。
つまり、マラソンと一緒です。
「ゴール」と「距離」の概念です。
ゴールがなければ無限ループに陥って永遠に終わりませんし、
ゴールがあっても進む度に距離が減らなければ、永遠にゴールにたどり着くことができない訳です。
なので、一歩進む度により単純化され距離が減る。(作業量が減る)
そして、進んでいけばいつか必ずゴールにたどり着く。(ループが終る)
この2つの約束事を守らなければなりません。
最も基本的な例題:再帰関数による階乗プログラム
階乗とは理系分野に進まずとも、高校の数学でチラッと勉強したこれです。僕もギリ覚えてます。
公式
n! = n * (n-1) * (n-2) * (n-3)…
例式
5! = 5 * 4 * 3 * 2 * 1 = 120
ようは「n」と、「n以下の整数」を、1まで全部かけることです。
これをループ処理、for文で表現すると以下のようになります。
# include <stdio.h>
int main()
{
int i; // カウンタ用
int n = 5; // 階乗する値
int result = 1; // 計算結果
for (i = 1; i <= n; i++) {
result = result * i;
}
printf("%dの階乗 = %d\n", n, result);
return (0);
}
---------------------------------------------------
出力結果
5の階乗 = 120
再帰関数で表すと、以下のようになります。
関数名は再帰 (英語 : recursive) から取って「rec」とします。
# include <stdio.h>
// 再帰関数
int rec(int n)
{
if (n == 1)
return (1);
return (n * rec(n-1));
}
int main()
{
int n = 5; // 階乗する値
int result; // 計算結果
result = rec(n);
printf("%dの階乗 = %d\n", n, result);
return (0);
}
---------------------------------------------------
出力結果
5の階乗 = 120
ループの場合
for (i = 1; i <= n; i++) {
result = result * i;
}
↓
再帰の場合
if (n == 1)
return (1);
return (n * rec(n-1));
上記のようにループ処理より、再帰関数の方がプロセスを減らして簡単にかける訳です。
今回は計算そのものが単純なんで差異も少ないですが、より複雑な処理になれば違いも大きくなってきます。
しかしこのように文字だけだと、処理の中で何が起こってるのか分かりづらく
感覚的に把握するのが難しいです。
分かるには分かるのですが、分かりやすくはないと個人的には思います。
なので再帰処理を視覚化してみました。

rec(5) は rec(5-1) を呼び出し、rec(4) は rec(4-1) を呼びだす…と言った具合に
次々に自身の関数を呼び出していきます。
- rec (5) 戻り値 (5 * rec(5-1)) rec(5-1) = (4 * 3 * 2 * 1)
- rec (4) 戻り値 (4 * rec(4-1)) rec(4-1) = (3 * 2 * 1)
- rec (3) 戻り値 (3 * rec(3-1)) rec(3-1) = (2 * 1)
- rec (2) 戻り値 (2 * rec(2-1)) rec(2-1) = 1
- rec (1) 戻り値 (1) 終点
このように関数は自身を呼び出すことを繰り返し、どんどん先に進みますが
進むごとに処理の内容はより単純になり、やがて終点 (n == 1) に行き着きます。
そして必ず呼び出されたのと同じ回数だけ、ぐるっと回って戻ってきます。
rec(1) は rec(2) に戻り、rec(2) は rec(3) に戻ります。最終的には rec(5) まで戻ります。
ですので、どちらかと言えば終点はゴールと言うより
戻る指標となる「折り返し地点」と言った感じでしょうか。
今回の場合、1まで到達して初めて合図が走り、戻り値の帰還が開始される訳です。
やっぱり難しく感じるナア。
文系出身だからかしら。
さて、再帰関数の基本はこれくらにして、次はツリー構造の話に移ります。
ツリーとは
「枝分かれして、段々細かくなっていく」という風に、木と作りが似ていることからツリーと呼ばれます。
root が頂点。一番上の箱のこと (root: 根)
node はルートを含めた箱、つまり要素全般のこと。箱 = ノード = 要素。全部一緒です (node: 節点)
leaf はそれ以上先がない一番下位の要素のこと (leaf : 葉)
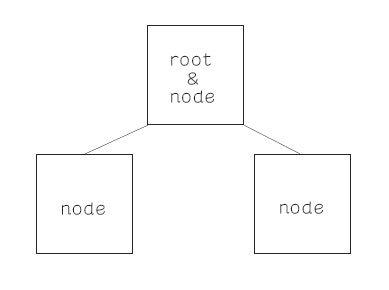
構造としてはこんな感じです。
下にいけば行くほど要素(ノード)が増えていきます。
また、線で繫がった上の要素と下の要素の関係を「親・子」といい、
上の要素から見た場合、下の要素を「子ノード」
下の要素からみた場合、上の要素を「親ノード」
と呼びます。
また、各ノード(葉以外)1つにつき、2つの子ノードを持っている作りになっているものを「二分木」と言い
(この場合、各ノードは左と右2つの子ノードを持っている。正確に言えばそれぞれのノードへのポインタ)
特に、現在操作している要素よりも
・小さい値の要素は左枝に
・大きい値の要素は右枝に
行き渡るように振り分けらたものを「二分探索木」といいます。
つまり、木の左ノードにいくほど値が小さくなり、右ノードにいくほど値が大きくなるようになっている二分木のことです。
宣言の仕方
ツリーの各要素は構造体として宣言します。
struct node{
int data; // この要素が保持している何らかのデータ
struct node *left_ptr; // 左要素へのポインタ
struct node *right_ptr; // 右要素へのポインタ
}
新たな要素を作成する度に、各種メンバの値を設定します。
新たに要素を作成するということは、子要素が存在しないので left_ptr と right_ptr は NULL で初期化します。
簡単ですね。これのどこが複雑なんだ、と思うかもしれませんが、
今は箱が3つだから単純にみえるだけで、箱が増えれば増えるほど入り組んで複雑になります。
またここではやりませんが、格納の仕方は二分探索木以外にも色々あります。
ポインタはCの鬼門とよく言われますが、個人的にツリーの方がよっぽど鬼門です。
まぁ人によるんでしょうが。
上の説明を見ていて思ったかもしれませんが、再帰とツリーは作りが似ています。
はじめの方ほど残りの数が多くなり、進んでいけば残りの数は減っていき、より単純化され、やがて終点に行き当たります。
ツリー構造の基本は以上です。
そして、いよいよここからが本題です。
前置きがやたらめったら長くなってしまいました。
ツリー構造に再帰関数を適用した場合、どのような処理が行なわれるのか。
それについて書いていきたいと思います。
ツリー構造における再帰関数
まず、0 ~ 10 までの数値を並べたテキストファイルを用意します。
以下をテキストファイルにコピーして「number.txt」を作成してください。
5
9
6
3
4
10
8
1
2
0
7
次にコードです。(ちょい長)
ソースの「PATH」には「number.txt」を保存しているフォルダを指定してください。
このプログラムは、ファイル内の数字を調べ、小さい数から順に画面に出力するプログラムです。
(※わかりやすさ重視のため、あえてコメントをかなり多めにつけています。あしからず)
/********************************************************************************
* number.c -- ファイルの数字を調べ、小さい数から順に出力する。
* ******************************************************************************/
# include <stdio.h>
# include <stdlib.h>
# include <string.h>
# include <ctype.h>
# define PATH "〜\\number.txt" // ~の部分は各自設定
struct node {
int value; // このノードが保持している値
struct node *left_ptr; // 左枝
struct node *right_ptr; // 右枝
};
// ツリーの頂点 root
static struct node *root = NULL;
/********************************************************************************
* make_tree -- ノードを作成し、ツリーに数値を挿入
*
* パラメータ
* node -- 現在のノード。ダブルポインタ(ポインタ変数へのポインタ)
* value -- テキストから取り出した、挿入する数値
********************************************************************************/
void make_tree(struct node **node, int value)
{
int result; // 数値の大小比較結果
// ノードが存在しない場合
if ((*node) == NULL) {
// 新しい領域を割り当てノードを作成する
(*node) = malloc(sizeof(struct node));
if ((*node) == NULL){
fprintf(stderr, "NULL");
exit (8);
}
// メンバを初期化
(*node)->left_ptr = NULL;
(*node)->right_ptr = NULL;
(*node)->value = value;
// make_tree関数を終了
return;
}
// テキストから取り出した数値をノードの数値と比較
// 現在のノードより大きかったら正。小さかったら負。等しかったら0
if ((*node)->value < value) {
result = 1;
} else if ((*node)->value > value) {
result = -1;
} else if ((*node)->value == value) {
result = 0;
}
// 現在の数値が既にあれば、新たなノードは作成せずmake_tree関数を終了
if (result == 0)
return;
// 大きかったら右枝に移動
if (0 < result) {
make_tree(&(*node)->right_ptr, value);
}
// 小さかったら左枝に移動
else {
make_tree(&(*node)->left_ptr, value);
}
}
/********************************************************************************
* check -- ファイル内の文字をチェックする。全て調べたら関数を終了。
********************************************************************************/
void check()
{
char number[100]; // テキスト内のまとまった数字(10など)を1つ格納
int index; // number配列のインデックス
int ch; // 現在の文字 (characterの意)
int value; // number配列の数字を整数に変換し格納
FILE *text_file; // 対象ファイル
text_file = fopen(PATH, "r");
if (text_file == NULL) {
fprintf(stderr, "Error: Uable to open %s\n", PATH);
exit (8);
}
// テキスト内の文字をすべて調べる
while (1) {
// 最初の数字をみつける
// スペースや改行は飛ばす
while (1) {
// ファイルから1文字読み取る
ch = fgetc(text_file);
// 数字、または終端文字に行き着いたらループを抜ける
if (isdigit(ch) || (ch == EOF))
break;
}
// 終端文字の場合、ループを抜け関数を終了
if (ch == EOF)
break;
// 文字配列の最初の要素に、取得した数字を挿入
number[0] = ch;
// 数字以外の文字や、改行・スペース、終端文字に行き着くまでループを繰り返し
// 取得した文字を number 配列に挿入
for (index = 1; index < sizeof(number); ++index) {
ch = fgetc(text_file);
if (!isdigit(ch))
break;
number[index] = ch;
}
// 文字列であることを示すため、終わりに終端文字を挿入
number[index] = '\0';
sscanf(number, "%d", &value);
// 取得した数値を make_tree 関数に渡す
make_tree(&root, value);
}
fclose(text_file);
}
/********************************************************************************
* print_value -- 再帰関数。ツリー中の数値を小さい順から画面に出力
*
* パラメータ
* now -- 出力するツリーのルート
********************************************************************************/
void print_value(struct node *now)
{
if (now == NULL)
return;
print_value(now->left_ptr);
printf("%d\n", now->value);
print_value(now->right_ptr);
}
int main()
{
check();
print_value(root);
return (0);
}
実行してみると、ちゃんと上から「0,1,2,3…」と小さい数から順番に整理され表示されたかと思います。
プログラムの流れ
※ここでは「文字としての数」と「整数としての数」の区別をつけるため
char型の数は「数字(number)」、整数型の数は「数値(value)」と言葉を使い分けています。
まずは check 関数によって、テキスト内の文字を調べて、ファイルから数字を取り出します。
スペースや改行区切りを見つけるまで1文字1文字配列に格納して調べることにより
1個の数字をまとめて取り出します(10など)。
数字を1個取り出す度に、make_tree 関数を実行してノードを新規作成し、その値をツリーに挿入します。
上記を繰り返し行い、ファイル内の文字を全て調べ終えたら、check 関数を終了します。
そして最後に print_value 関数を実行して、完成したツリーの値を画面に出力します。
出力すると0から順に表示されるので、つい一番最初の要素 root に「0」が格納されている、
と勘違いしてしまいそうですが、そうではありません。
root には一番最初に取り出した数値「5」が格納されています。
それを print_value 関数によって小さい数から順に出力しているに過ぎません。
では、具体的にツリー構造体にはどのように各々の数値が格納されているのでしょうか。
視覚化するとこんな感じです。
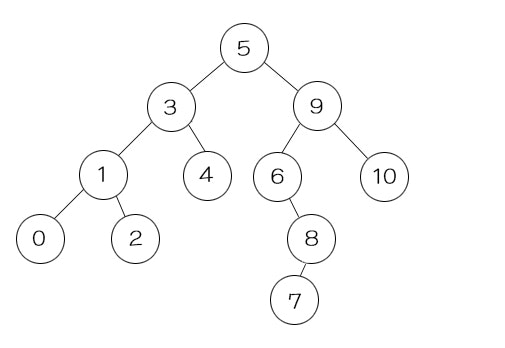
5を中心として、それより小さい数は左側へ。大きい数は右側へ振り分けられています。
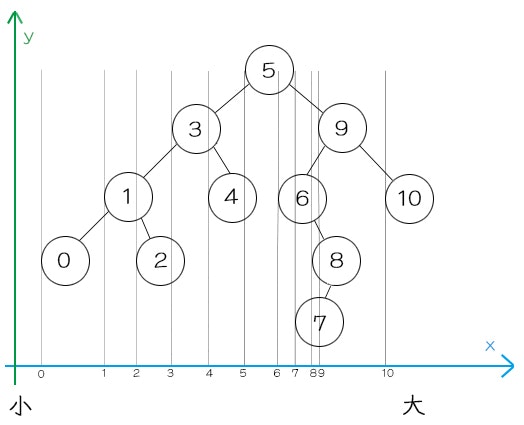
y軸(縦)としてみた場合、順番はデタラメにみえますが
(実際テキストファイルに記入されている順番に依存するので、デタラメも同然です)
x軸(横)としてみた場合、ちゃんと左から順に「小さい数→大きい数」となるように格納されるわけです。
なので、小さい数から順にデータを出力したかったら、左から順に出力すれば数値順に出力できる訳です。
(本当ならそれぞれの数値の差が1なので、グラフ的には等間隔になるべきなんでしょうがそこまで器用に画像を作れませんでした……汗)
二分探索木では「格納された順番」は重要ではなくて、「振り分け方」が重要になります。
さて、本題の再帰関数を使った部分である print_value 関数 についてです。
print_value 関数
void print_value(struct node *now)
{
if (now == NULL)
return;
print_value(now->left_ptr);
printf("%d\n", now->value);
print_value(now->right_ptr);
}
なんじゃこりゃ(・ 。・;)
参考書で(著作権的な観点から内容を微妙に変えてあります)特に細かい説明もなく出て来て通り過ぎたんで
最初みたとき目がてんになりました。3度見してもわかりません。
バカにもわかるように、はしょらないで説明してくれ!><
ググってもこれについて質問してる人がいなかったんで、恐らくググるまでもなく分かって当然の内容なんだと思います。
ですが今後、僕並みの人(失礼)が勉強した時困らないように、この処理の意味を情報として残しておきます。
print_value 関数の処理の流れ
まず print_value(now->left_ptr);
の引数に、左枝へのポインタを渡すことで、再帰を繰り返して延々と左枝へ移動し、
一番外側の左枝の要素へとたどり着きます。
一番左ということは、一番小さい値ですね。
「0」を格納している要素のことです。
そしてまたも (now->left_ptr) で左枝へのポインタを渡すのですが、一番下位の要素のため、
当然子ノードはないので引数の値は NULL になります。
今回の折り返す指標となる終点は 「NULL 」なので、それ以上進まずに「0を操作する関数」へと戻ります。
戻ったら次に printf を実行し、そして右枝へと移動します
0の要素を操作する関数
print_value(now->left_ptr); ← NULL に当たって戻ってくる
printf("%d¥n", now->value); ← 自身の値0を画面に出力
print_value(now->right_ptr); ← 右枝へ移動
「0」は一番下位の要素なので、左枝と同様に右枝もありません。
なので終点である NULL に行き当たり、また return で戻ってきます。
そして「0を操作する関数」は処理を終えます。
この関数に戻り値はありません。
「画面に出力」して、それで終了です。
終了した関数がどうなるかと言うと、当然「自身を呼び出した関数」の元へと帰ります。
「0の要素を操作する関数」を呼び出したのは「1の要素を操作する関数」です。
関数は print_value(now>left_ptr) で呼び出したのですから、次に実行される処理は printf です。
1の要素を操作する関数
print_value(now->left_ptr); ←「0の要素を操作する関数」を終了し戻ってくる
printf("%d¥n", now->value); ← 自身の値1を出力
print_value(now->right_ptr); ← 右枝に移動
これにより右枝の「2の要素を操作する関数」へと移動します。
2の要素は、また子ノードを持たない一番下位の要素なので、先程と全く同じです。
- 左枝を調べる
- 調べ終えたら戻ってくる
- 値を出力する
- 右枝を調べる
- 調べ終えたら戻ってくる
- 関数を終了して、自身を呼び出した関数の元へと戻る
これが全体の流れです。
まとめて言えば
「ある要素の左枝先を全部調べ終えたら、自身の値を出力し、次にその要素の右枝先の要素を全部調べる」
と言う順番です。
一番中心の要素となるのは root である「5」ですが、5以外の場合でもやってることは全部一緒です。
例えば「9」に行き着くと、9の左枝先の要素「6、7、8」を全て調べて、それが終ったら9を出力し、
そして右枝の要素である「10」調べる、といった具合です。
こうして関数はツリーの一番下にいき、そしてまた徐々に上へと戻ってきます。下に行っては上へ戻りを繰り返し
最後に一番最初に呼び出した「5の要素を操作する関数」の
print_value(right_ptr);
に戻り、処理の一番下に到達して print_value 関数が完全に終了します。
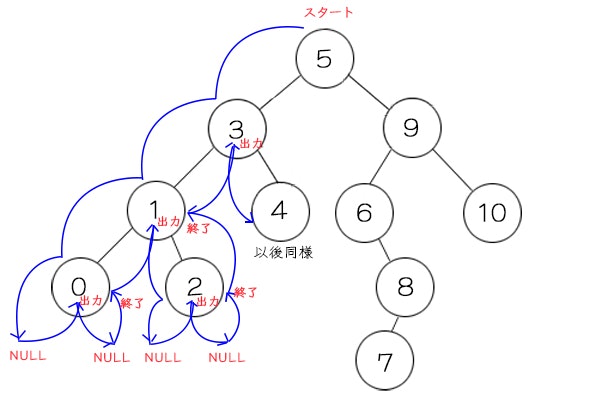
流れを図にするとこんな感じになります。
何これめっさ難しい。
あの短いコードでこんな複雑なことをしていたんですね。
それをたった3, 4行で書けてしまうなんて
考えた人天才だろ、と大袈裟に感心してしまいます。
二分探索木を使えば、例えば「4の値の要素」を探したい時は左側の枝だけ調べればよく、
残りの半分である右側の枝は一切調べる必要がないので、処理効率が良い訳です。
しかし、再帰関数は結構容量を喰います。
最初の階乗の例で言えば、再帰の度に同じ名前の変数「n」を連続して使用しますが、
それぞれの n は全くの別物で、名前が同じでもアドレスを確認すると一つ一つ違う領域に割り当てられていることがわかります。
つまり再帰の回数が多ければ多い分だけ、どんどん領域を喰っていく訳です。
なので、うまく使いこなせたとしても短く書けて便利だからと言って、やたらめったら再帰を多様するのはやめといた方がよさそうです。
終わりに
僕は「1以下の数」と言うモノとしては存在しない、概念上の数字を扱う分数という考え方が苦手なのですが
何だか再帰関数もそれと似たものを感じます。
日常生活の中では、あまりしない脳の使い方をしますよね。
やってりゃそのうち慣れるんでしょうか。
とりあえず、初心者の初心者による、初心者のためのツリー構造で扱う再帰関数のまとめは以上になります。
一から詳しく解説しようと思ったので、思いのほか長くなってしまいました。
尚、筆者はまだ勉強中の素人プログラマです。
かなり手探りで書いてますので、間違ってるところがあったらごめんなさい。
何かミスがあれば指摘してくれると有り難いです。