背景
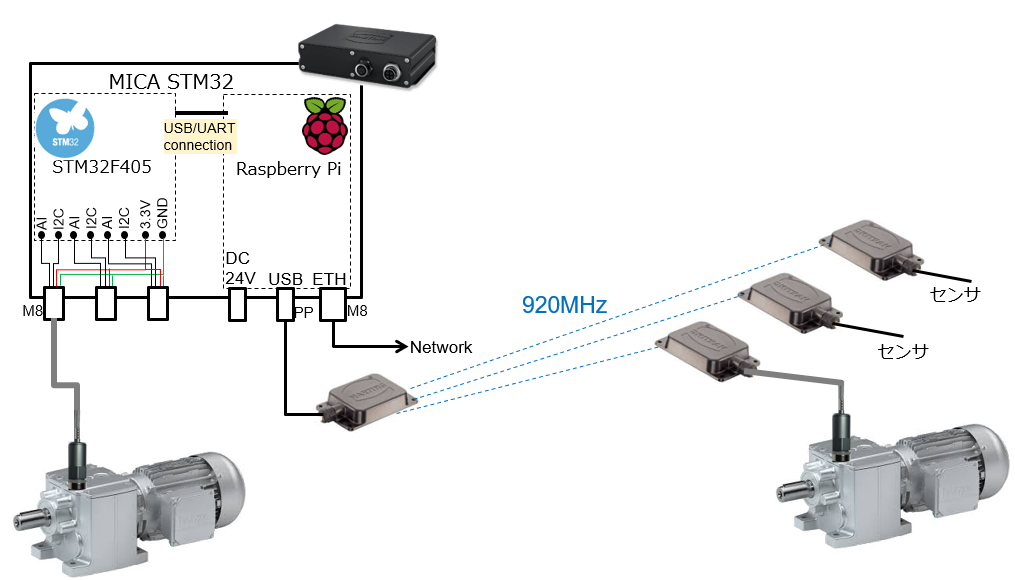
https://www.pi4industry.com/products/remote-mica/
すでにMEMSセンサーとラズパイを組み合わせたモータの故障予知診断システムもリリースから1年が経ち、石油プラント、自動車工場、製鉄所、工作機械、ロボットなど幅広い分野で使って頂いております。アナログデバイセズのADXL1002をベースとした高性能加速度センサにより、微小振動を10000Hzまでの高周波まで収集できるため、これまで異音等がでるまで分からなかったモータの故障兆候を何か月も前に発見できるようになりました。
故障判定の現状
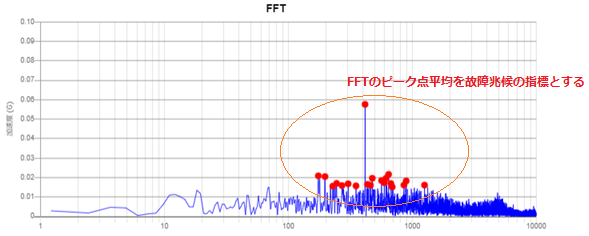
微細な故障兆候の検出には高性能センサと共に、収集したデータを適切に解析するノウハウが欠かせません。ハーティングが無償提供する故障診断Webアプリでは、加速度計測値をFFTした上で適切な周波数エリアを設定し、そのピーク点何点かの平均値をプロットします。そこで急激な変化点が現れたら異常を疑います。上述したプロジェクトではそれ以外にもエンベロープ処理をした値をベースにした評価指標など、お客様のこれまでのオペレーションノウハウを生かした計算ロジックをカスタム開発させていただいてきました。
機械学習, 深層学習へのモチベーション
従来の周波数スペクトラムベースの解析には長い歴史と多数の成功事例が報告されているものの、"ギヤ故障は加速度波形に周期的な振動スパイクがでる”とか”ベアリング故障はエンベロープ波形のこの周波数に山が立つ”といった長年の経験をもとに評価指標を設定するケースが多く、これまでのデータ蓄積がないアプリケーションの場合、パラメータチューニングに時間がかかるという結構致命的な問題があります。
実は機械学習を使えばそれらのチューニングが不要で、文字通り半自動的に故障予知指標を定義できることが、これまでいくつかの機械学習プロジェクトでわかってきました。
今回の事例
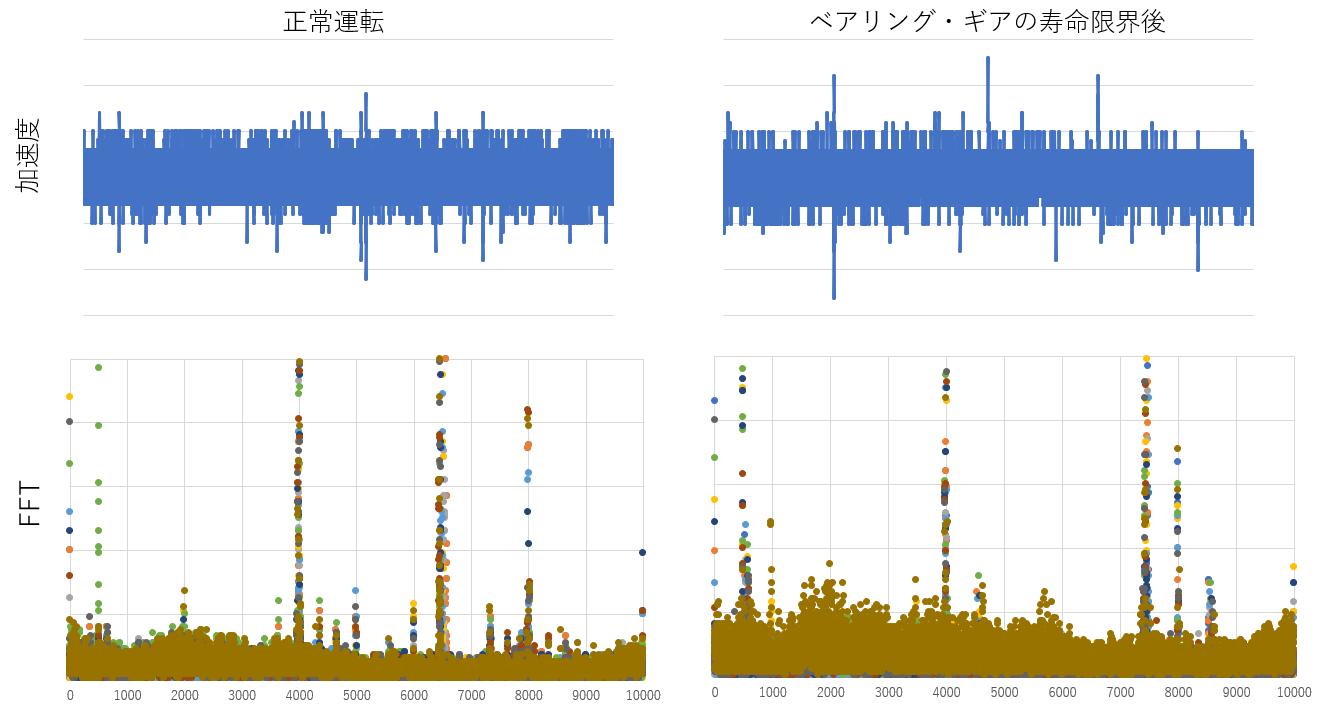
ここに長期間根気よく大型機械のストレス運転を行い、ベアリング・ギア等のの公称寿命を迎えたデータがあります(公称寿命を超えているだけで必ずしも故障状態ではありませんが)。”大型”とはいえ非常に静かに運転するデリケートな機械であり、0.1~0.2G程度の加速度でしか振動しません(敢えて値は隠しておりますが)。左が正常時の運転波形、右がストレス試験後の公称寿命を超えた状態の運転波形です。また上の波形が加速度値、下がそのFFT結果です。目で見る分には加速度波形からはほとんど差異は見られませんが、FFT結果では寿命限界後の方が全体的に山が盛り上がっています。ここまで差異があればFFT値で故障兆候判定ができそうですが、この機械にはいくつか共振点が存在し且つ、それらのFFT値が非常に高く、またその値は正常時、異常時でもさほど変わりません。残念ながら標準機能である”ピーク平均法”でやってしまうと、これらの極大値が平均値を一気に押し上げるため誤判定が頻発してしまいます。従来は共振点を外すなどのカスタム対応でうまく評価指標を定義してきましたが、今回はこの事例に機械学習のアプローチを適用してみたいと思います。
特徴量の抽出
機械学習では、対象を"十分に”表現する特徴量が必要です。振動計測に機械学習を適用する場合、時系列データをそのままは扱えない(時系列をそのまま扱う手法は後日別記事で!)ので、一般的には時系列の特徴を表す実効値平均、実効値最大値、波高率(実効値最大/実効値平均)、FFTスペクトラムの適当な周波数幅内の平均、ピーク値、エンベロープ変換スペクトラムの最大値などを上手に組み合わせて特徴量を形成します。
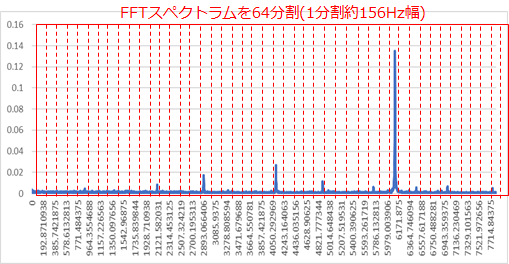
今回はもともとのFFTピーク平均手法に近いアプローチとするため、1~10000Hzを64分割し各分割区間のピーク値64個を特徴量とします。
PCA(主要因分析)による次元削減
特徴量が決まれば、特に今回は十分な数の正常データと異常データがありますので、一般的には機械学習の教科書を片手にあとはサポートベクタ(SVM)やランダムフォレストといった手法を使って正常と異常を分ける分類器を作ります。分類器はオープンソースライブラリScikit learn(https://scikit-learn.org/stable/ )を使えばものの数行のPythonプログラムで書けてしまいます。
今回はその前に特徴量をプロットし正常データと異常データの特徴量の分布を確かめてみたいと思います。といっても64次元のプロットは目で確認できませんので、PCA(主要因分析)という手法を使って64次元から可視化できるように2次元に次元削減します。詳細は数ある機械学習の教科書に譲りますが、PCAでは最も特徴量の情報が継承されるように特徴量次元削減(線形変換)を行います。もう少し数学的いうと分散が最大になるようなベクトル方向に第1成分(新特徴量)を定義し、それに直行するベクトルでさらに分散が最大になる方向を第2成分を定義します(2次元への次元削減であればこれで終わりです)。PCAの次元削減でどれくらいの情報量が継承されるのかは寄与率という値を計算すればわかりますが、今回の場合は2次元に削減しても92%の特徴量情報が残っています。
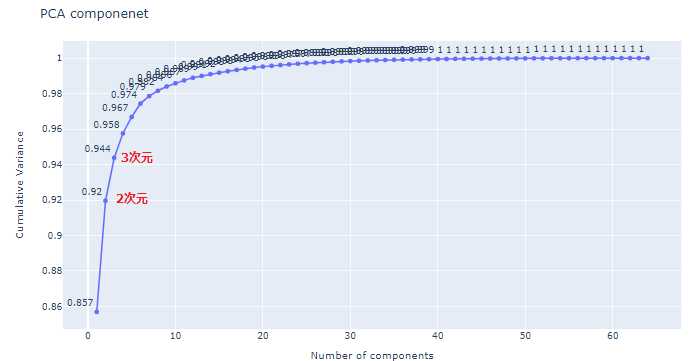
PCAによる新特徴量のプロット
PCAによって次元削減された2つの新特徴量(第1主成分と第2主成分)をプロットしてみましょう。
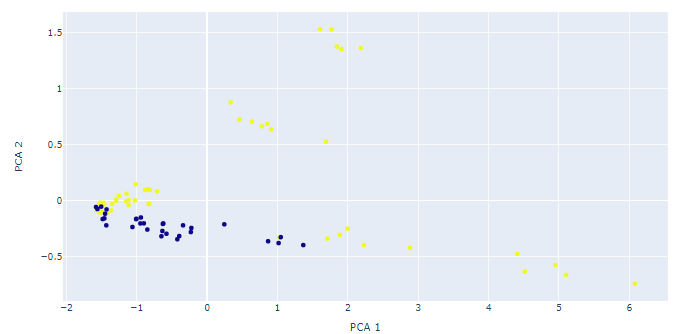
青点が正常データ、黄点が異常データです。64から2次元に次元削減したにもかかわらず綺麗に分かれてくれました。実は今回のデータには"異常"だけではなく公称寿命を超えてもスムーズに稼働したものと異音等のアラームが発生したものと異なるラベルがついていたのですが、右下方向に延びる点群が前者、上方向に延びる点群が後者であることも分かっています。ちなみに3次元のプロットも描いてみましたが、3次元プロットするメリットはあまりなさそうです。
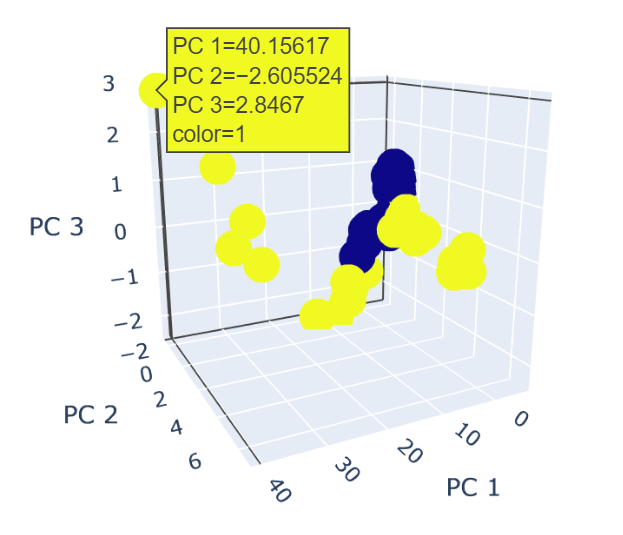
分類器の設計
上記の2次元プロットを見る限り、第1主成分(横軸)と第2主成分(縦軸)に適当な閾値を設ければ十分に説得力のある故障予知のロジックを作れそうですが、あくまで機械学習の数学的アプローチにこだわってScikit-learnで分類器を作ってみます。
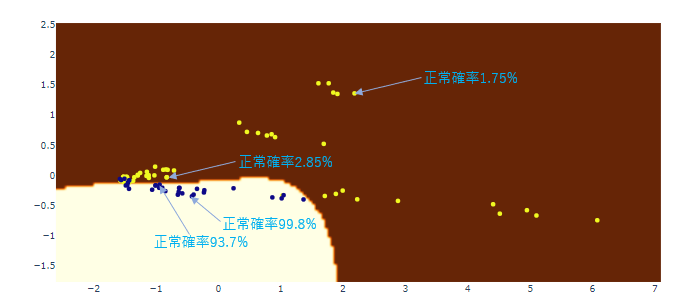
SVM(rbfカーネル)を使ってほぼきっちり分けてくれる分類器が作れました。Scikit-leanのSVMモデルは判定確率も算出してくれるので、例えば境界線に近い点については正常値でも"故障に近い”度合いを表現してくれるのではないかと期待したのですが、いずれの点も自信満々な値になっており寿命予測には使えなさそうです。もっとも寿命予測を求めるのであれば、分類精度を犠牲にしても線形SVM(境界線が直線)を使い、境界線からの距離を指標にする方が良い結果が得られるでしょう。rbfカーネルで非線形マッピングをしてしまうと元の線形空間での距離が簡単に計算できないためです。
次元削減の功罪
実は単純に分類器性能を求めるのあればもとの64次元の特徴空間で分類器を計算すべきです。しかしながら、今回次元削減後のプロットで分類器を考えたのはいくつか理由があります。
次元削減の一番大きな利点は可視化できることです。言い換えると、簡単に説明できる納得感のあるモデルが作れることです。64次元超平面上に曲面があってその上が異常(64次元なので上も下もないんですが)なんて言ってもまず信用してもらえません。また今回はきれいに正常点と異常点が分かれましたが、実際複雑に混ざり合っていても次元が大きくなれば点間の距離も増大する(次元の呪いと呼ばれます)ため、様々なモデルを駆使すれば高い精度の分類器が作れてしまいます。しかしながら、少ないデータや特定の試験機からしか得られないケースが多い故障診断の現場では、そのモデルは汎化性能の低い過学習モデルに陥っている可能性が高いです。PCAで次元削減+可視化をしておいて、正常から異常に至るトレンドをプロットで確認し、合わせて"故障に近い”も判定方法も考えるというアプローチはは実際の導入現場では安心感があります。
また次元削減には測定ノイズの除去という重要な側面もあります。PCAでも大きな外れ値には引っ張られてしまいますが、基本的に情報量が少ない特徴量を無視することにより計測ノイズの影響を低減できることが知られています。これは教師なしでの異常値検知の主流になりつつあるオートエンコーダによる次元削減でも重要役割を果たします。
なおPCAは線形変換ですので、定義される主成分は元の特徴量に重みをつけて足したものです。従ってラズパイのような計算能力の低いエッジコンピュータでも十分実装できるのも大きな利点といえるでしょう。
おわりに
今後も弊社で実績のある機械学習・深層学習のアプローチを紹介していきます。Scikit-learnやTensorFlowなどのオープンソース工学ツールのおかげで、専門知識のない最終ユーザーでもお金を掛けずに最新数学理論を現場に適用できるようになりました。機械学習で成果を出すコツは、対象機器毎に最適なアプローチを地道に試行錯誤することです。One fits allを謳う高額なAIパッケージも目にしますが、長年のオペレーションノウハウと地道な検証を反映した学習モデル以外で大きな成果を上げることはありえません。ハーティングでは、そんな地道なフルカスタム学習モデルを目指すユーザー様のお手伝いをさせていただいております。
謝辞
本稿についてアドバイスをいただきましたAidemy実践データサイエンス講座https://premium.aidemy.net/data-science
の先生方に厚く御礼申し上げます。
(文責・お問合せ先: ハーティング株式会社 能方研爾 kenji.nogata@harting.com)