BabylonJS Node Geometry のクラスを使ってコードでメッシュを作る

ノード ジオメトリ クラス

BabylonJS では Babylon.js Node Geometry Editor が提供されておりノードベースでジオメトリを生成できますが
各ブロックに対応するクラスが存在しコードを書くことによってもジオメトリ生成することができます。
今回はコードベースで、すり鉢状のメッシュを作成してみます。

ブロックそのもののクラスが用意されているものもあれば Inputs や Contextual, Math は複数の種類が1つのクラスにまとめられています。

最後にブーリアンブロックを適用しますが、引き算する方の図形の法線をあらかじめ反転しておいて断面の法線が自然に外側を向くようにしています。

以下のコードは 2024年12月1日の Babylon.js Playground 7.37.0(WebGL2) Javascript で動作したことがあります。

12/2: 動作はするが _v3 でカウンタが上がっていなかったので修正。

const createScene = function () {
    const scene = new BABYLON.Scene(engine);
    const camera = new BABYLON.ArcRotateCamera('camera1',
        0, 0, 5,
        new BABYLON.Vector3(0, 0, 0), scene);
    camera.position = new BABYLON.Vector3(2, 5, -5);
    camera.attachControl(true);
    const light = new BABYLON.HemisphericLight('light', new BABYLON.Vector3(0, 1, 0), scene);
    light.intensity = 0.7;
    {
        let count = 0;
        const _in = (val, type) => {
            const bl = new BABYLON.GeometryInputBlock(`bl${count}`, type);
            bl.value = val;
            count += 1;
            return bl;
        };
        const _float = (val, to) => {
            const bl = _in(val, BABYLON.NodeGeometryBlockConnectionPointTypes.Float);
            bl.output.connectTo(to);
        };
        const _v3 = (x, y, z, to) => {
            const bl = _in(new BABYLON.Vector3(x, y, z), 
                BABYLON.NodeGeometryBlockConnectionPointTypes.Vector3);
            bl.output.connectTo(to);
        };

        const ng = new BABYLON.NodeGeometry('node');
        {
            const bbase = new BABYLON.CylinderBlock('bobj');

            const bcut = new BABYLON.CylinderBlock('bcut');
            const bnormal = new BABYLON.GeometryInputBlock('bnormal');
            bnormal.contextualValue = BABYLON.NodeGeometryContextualSources.Normals;

            const bmul = new BABYLON.MathBlock('bmul');
            bmul.operation = BABYLON.MathBlockOperations.Multiply;
            const bpos = new BABYLON.GeometryInputBlock('bpos');
            bpos.contextualValue = BABYLON.NodeGeometryContextualSources.Positions;

            const badd = new BABYLON.MathBlock('badd');
            badd.operation = BABYLON.MathBlockOperations.Add;
            const bsetnormal = new BABYLON.SetNormalsBlock('bsetnormal');
            const bsetpos = new BABYLON.SetPositionsBlock('bsetpos');

            const bbool = new BABYLON.BooleanGeometryBlock('bbool');
            bbool.operation = BABYLON.BooleanGeometryOperations.Subtract;

            const out = new BABYLON.GeometryOutputBlock('out');

            _float(0.5, bbase.height);
            _float(2.0, bbase.diameter);

            _float(0.5, bcut.height);
            _float(1.9, bcut.diameter);
            _float(0.0, bcut.diameterBottom);

            bnormal.output.connectTo(bmul.left);
            _v3(-1, -1, -1, bmul.right);
            bmul.output.connectTo(bsetnormal.normals);
            bcut.geometry.connectTo(bsetnormal.geometry);

            bpos.output.connectTo(badd.left);
            _v3(0, 0.02, 0, badd.right);
            badd.output.connectTo(bsetpos.positions);
            bsetnormal.output.connectTo(bsetpos.geometry);

            bbase.geometry.connectTo(bbool.geometry0);
            bsetpos.output.connectTo(bbool.geometry1);
            bbool.output.connectTo(out.geometry);

            ng.outputBlock = out;
        }
        ng.build();
        const mesh = ng.createMesh('ngmesh', scene);
    }

    return scene;
};

実行結果
円筒がすり鉢状に削れたメッシュが出来上がります

対応するノード
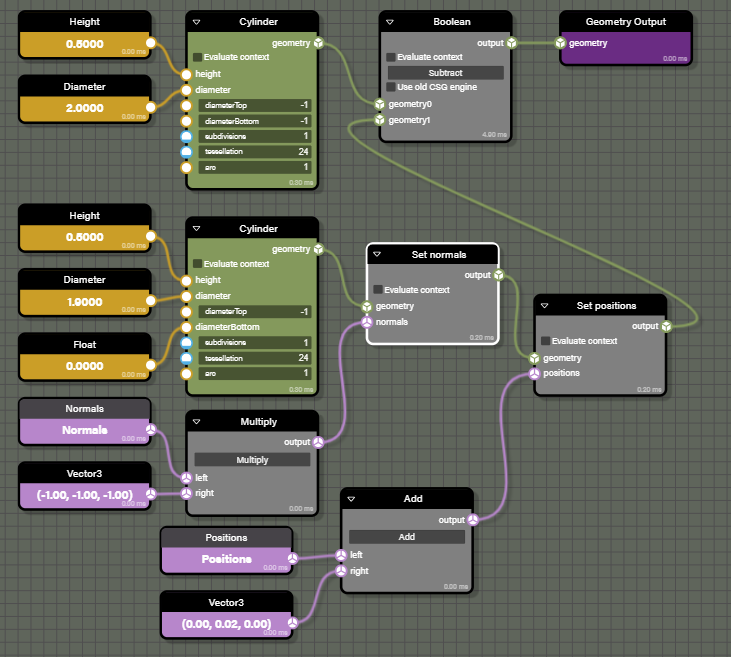Node Geometry Editor で同じ構成のグラフを組んだ場合(ブロックの個別名は違います)

Node Geometry Editor で法線表示した場合の見え方
Node Geometry Editor で ←|→ボタン で法線表示にした場合

リンク

• Node Geometry
  https://doc.babylonjs.com/features/featuresDeepDive/mesh/nodeGeometry/