2. データの概念: 単純型 (Simple Types)
2.1. 順序型 (Ordinal Types)
・順序関数の引数の型は？
関数 Succ(), Pred(), Ord() は順序関数と呼ばれる、ちょっと特殊な関数です。パラメータはいずれも順序式で、任意の順序型を受け付けます。
function func(X: Ordinal): Result;
上記のような形式の関数になるのですが、Ordinal という型が存在するわけではないので、ユーザー定義の順序関数を作る事はできません。もちろん、オーバーロード関数を作る事は可能です。
See also:
2.2. Boolean 型 (Boolean Types)
2.3. Integer 型 (Integer Types)
・剰余演算子について
他の言語を見渡してみると、剰余の演算子 と呼ばれるものには、REM (Remainder) と MOD (Modulo) の 2 種類があります。
| 言語 | REM | MOD |
|---|---|---|
| 標準 Pascal | N/A | mod |
| Delphi | mod | N/A |
| Modula-2 (PIM) | MOD | N/A |
| Modula-2 (ISO) | REM | MOD |
| Ada | rem | mod |
| C/C++ | % | N/A |
オペランドがどちらも正の数の場合には演算結果は同じになりますが、被除数が負の数の場合には演算結果が異なります。
A MOD B (標準 Pascal)
標準 Pascal の MOD の演算結果です。
| A | B | V |
|---|---|---|
| 31 | 10 | 1 |
| -31 | 10 | 9 |
| 31 | -10 | エラー |
| -31 | -10 | エラー |
除数に負の数を指定するとエラーになります。
A REM B
Delphi / Modula-2 (PIM) の MOD、 Modula-2 (ISO) / Ada の REM の演算結果です。
| A | B | V |
|---|---|---|
| 31 | 10 | 1 |
| -31 | 10 | -1 |
| 31 | -10 | 1 |
| -31 | -10 | -1 |
A MOD B
Modula-2 (ISO) / Ada の MOD の演算結果です。GNU Pascal や、Free Pascal の ISO モードもこちらです。
| A | B | V |
|---|---|---|
| 31 | 10 | 1 |
| -31 | 10 | 9 |
| 31 | -10 | 例外 or -9 |
| -31 | -10 | 例外 or -1 |
REM と MOD を Delphi のコードで書くとこうなります。
function Rem2(A, B: Integer): Integer;
begin
Result := A mod B;
end;
function Mod2(A, B: Integer): Integer;
begin
Result := A - (A div B) * B;
if Result < 0 then
Result := Result + B;
end;
See also:
・論理演算子について
xor, shr, shl 演算子は Turbo Pascal 1.0 から存在しました。同様に BLS Pascal では EXOR と SHIFT 演算子があり、SHIFT 演算子は正の数で左シフト、負の数で右シフトでした。
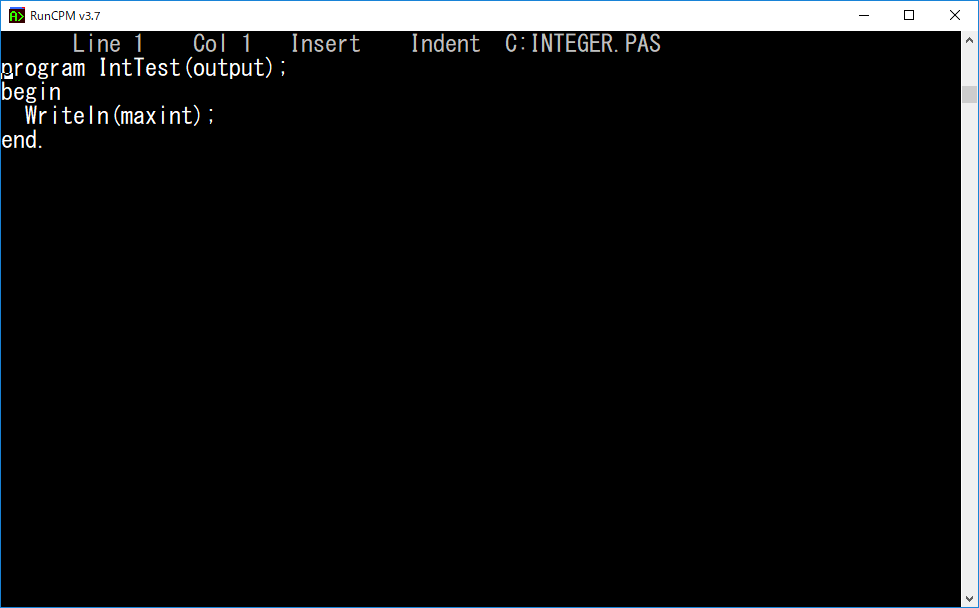
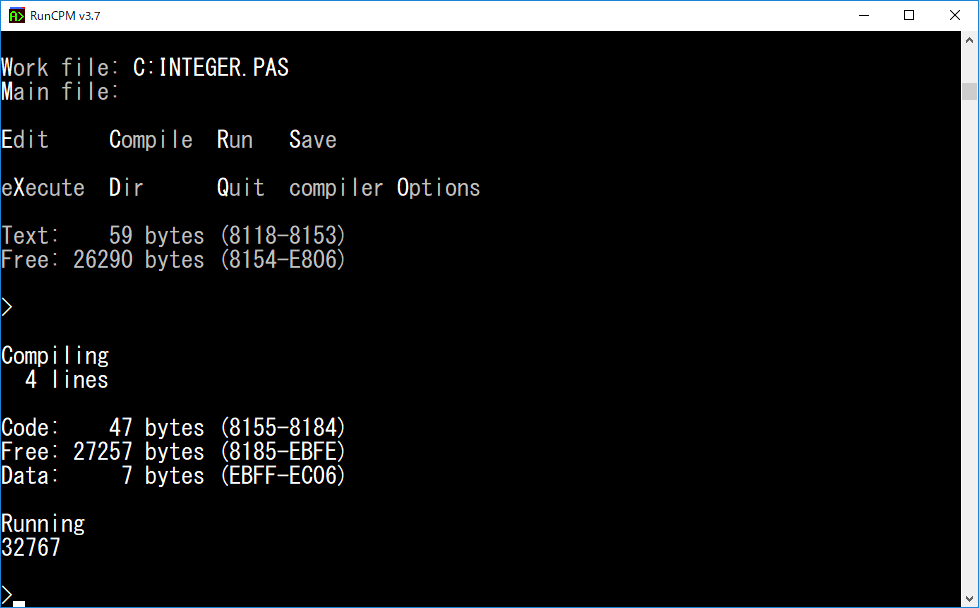
・MaxInt について
定義済み定数に MaxInt があり、その値は処理系依存です。Integer が 32 ビットとは限りません。
Turbo Pascal の Integer は 16 ビットでした。
See also:
2.4. Char 型 (Character Types)
2.5. Real 型 (Real Types)
Real48 はクラシック Pascalが稼働していた CDC 6000 シリーズにネイティブな 48 ビットの実数型です。
Delphi も Delphi 3 まで Real 型は 48bit でした。Delphi 4 以降、Real 型は 64bit になり、後方互換性のための Real48 型が残されました。
Real 型を 48bit 実数型にするには {$REALCOMPATIBILITY ON} コンパイラ指令を用います。
See also:
(2.6.) 順序型変数の初期化
索引
[ ← 1. 記法: トークンと区切り文字〔裏〕 ] [ ↑ 目次へ ] [ → 3. プログラムヘッダと宣言部〔裏〕 ]