Go to Qiita Advent Calendar 2024 Top
LoginSignup
7
2

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@ht_deko(Hideaki Tominaga)

<8> 集合型 (標準 Pascal 範囲内での Delphi 入門)

Last updated at Posted at 2019-03-11

8. 集合型 (Sets)

集合は、同一の順序型の値の集まりです。値に順序はありません。また、同じ値を格納する事にも意味はありません。集合型は空集合を表す事もできます。集合は抽象化されたビット配列です。

集合型 = 
  [packed] set of 基底型.
基底型 =
  順序型.

但し Pascal は通常、集合型に指定できる順序型の範囲を制限していて、非常に小さいものしか定義できない場合もあります。

type
  TSomeInts = 1..250;
  TIntSet1 = set of TSomeInts; (* 部分範囲型の集合                        *)
  TIntSet2 = set of 1..250;    (* こう書いても同じ                        *)
  TIntSet3 = set of 0..255;    (* 256 個の基底型                          *)
  TIntSet4 = set of 0..256;    (* NG: 基底型の要素数が 257 個ある         *)
  TIntSet5 = set of 200..300;  (* NG: 基底型の要素の値が 256 を超えている *)

Delphi の場合、基底型の要素数が 256 を超えてはいけませんし、その要素が取り得る値も 0～255 の範囲内である必要があります。

集合型の定義と同時に変数宣言する事が可能です。

var MySet: set of 1..10;

例えば文字型の集合であれば、

var MyCharSet: set of Char;

とする事ができます。但し、Char 型 が常に 8 ビット (0～255) であるとは限りませんので、この書き方には注意が必要です。

See also:

8.1. 集合構成子 (Set Constructors)

集合値は要素の記述をカンマ , で区切るか、low..high 形式の範囲を指定し、全体を [ ] で括ったものです。これを集合構成子といいます。

集合構成子 = 
  "[" [集合要素 {"," 集合要素} "]".
集合要素 = 
  式 [".." 式].

以下は集合構成子の例です。

[1, 5, 10, 50, 100];
[i + 1, i + 2];
['A'..'Z'];
['0'..'9', '#', '*'];

集合構成子は他の集合の型との適合性を持つようにするため、パックの状態を持ちません (不定)。

See also:

8.2. 集合演算子 (Set Operations)

(8.2.1.) 集合の代入

X を集合型変数、E を集合式とすると、

  1. E の要素がすべて X の基底型に含まれる。
  2. X と E が共に set of あるいは X と E が共に packed set of。
X := E;

上記条件を満たした場合に代入が可能です。

Delphi では次の組み込みルーチンも使えます。

手続き 説明
Include(S, I) S := S + [I]; と同等
Exclude(S, I) S := S - [I]; と同等

See also:

(8.2.2.) 集合の演算

A と B が同じ集合型の場合に次の集合演算が可能です。

演算 集合 数学記号 説明
A + B 和集合 A ∪ B A と B のすべての要素の集合
A - B 差集合 A ＼ B A にあって B にない要素の集合
A * B 積集合 A ∩ B A と B に共通の集合
Setstest.pas
program SetsTest1(output);
type
  TDayOfTheWeek = (Mon, Tue, Wed, Thu, Fri, Sat, Sun);  
var
  A, B, C: set of TDayOfTheWeek;
  Day: TDayOfTheWeek;
begin
  A := [Wed..Fri];
  B := [Mon, Wed, Fri, Sun];

  C := A + B;
  for Day:=Mon to Sun do
    begin
      if Day in C then
        begin
          Write(Ord(Day));
          Write(' ');
        end;  
    end;
  Writeln;
  
  C := A - B;
  for Day:=Mon to Sun do
    begin
      if Day in C then
        begin
          Write(Ord(Day));
          Write(' ');
        end;  
    end;
  Writeln;

  C := A * B;
  for Day:=Mon to Sun do
    begin
      if Day in C then
        begin
          Write(Ord(Day));
          Write(' ');
        end;  
    end;
  Writeln;
end.

上記プログラムの実行結果は次のようになります。

    0   2   3   4   6
    3
    2   4

(8.2.3.) 集合の比較演算

次の比較演算も行えます。

演算 意味 数学記号 説明
e in A 帰属関係 e ∈ A e が A の要素であれば True
A = B 等しい A ＝ B A と B が同じ集合であれば True
A <> B 等しくない A ≠ B A と B が異なる集合であれば True
A <= B サブセット A ⊂ B A が B の部分集合であれば True
A >= B スーパーセット A ⊃ B B が A の部分集合であれば True

※ in 演算子は順序型に対しても使えます。

SetsTest2.pas
program SetsTest2(output);
type
  TDayOfTheWeek = (Mon, Tue, Wed, Thu, Fri, Sat, Sun);  
var
  A, B, C: set of TDayOfTheWeek;
  BoolStr: array [Boolean] of packed array [1..5] of Char;
  v: Boolean;
begin
  BoolStr[True ] := 'True ';
  BoolStr[False] := 'False';

  A := [Wed..Fri];
  B := [Mon, Wed, Fri, Sun];
  C := [Mon..Sun] - B; (* [Tue, Thu, Sat] *)
  
  { e in A }
  v := Mon in A;
  Writeln(BoolStr[v]);
  
  { A = B }
  v := (A = B);
  Writeln(BoolStr[v]);

  { A <> B }
  v := (A <> B);
  Writeln(BoolStr[v]);

  { A <= B }
  v := (A <= B);
  Writeln(BoolStr[v]);
  
  { A >= B }
  v := (A >= B);
  Writeln(BoolStr[v]);

  { A <= B + C }
  v := (A <= B + C);
  Writeln(BoolStr[v]);

  { B + C >= A }
  v := (B + C >= A);
  Writeln(BoolStr[v]);
end.

上記プログラムの実行結果は次のようになります。

False
False
True
False
False
True
True

次のコードは、数値を 3 度入力して条件に合致したら Hello!World. と表示するコンソールアプリケーションです。

SetsTest3.pas
program SetsTest3(input, output);
var
  a, b, c: Integer;
begin
  repeat
    Writeln('*');
    Readln(a);
    Readln(b);
    Readln(c);

    if (a = 2) and (b = 2) and (c = 2) then { (A) }
      Write('Hello!');

    if [a, b, c] = [2] then                 { (B) }
      Writeln('World.');

  until ([a, b, c] = [0]); { すべて 0 を入力すると抜ける }
end.

(A) と (B) の条件式は等価なので、Hello! だけ表示されたり World. だけ表示されたりする事はありません。

*
1
2
3
*
1
1
1
*
2
2
2
Hello!World.
*
3
3
3
*

同様に、次のような比較演算が可能です。

(A) (B) 条件
if (a = 2) and (b = 2) and (c = 2) then if [a, b, c] = [2] then a,b,c すべてが 2
if (a <> 2) and (b <> 2) and (c <> 2) then if not (2 in [a, b, c]) then
または
if not([a, b, c] >= [2]) then 		a,b,c すべてが 2 ではない
if (a = 2) or (b = 2) or (c = 2) then if (2 in [a, b, c]) then
または
if [a, b, c] >= [2] then 		a,b,c どれかが 2
if (a <> 2) or (b <> 2) or (c <> 2) then if [a, b, c] <> [2] then a,b,c どれかが 2 ではない

集合を使った比較演算は完全論理評価になるため、a,b,c が関数だった場合にはすべて評価されてしまいます。副作用に気を付けましょう。

See also:

(8.2.4.) ビット集合 (Bitset)

集合は抽象化されたビット配列です。Delphi だと同じサイズの型へキャスト (10.7.2 節) できます。

BitTest.pas
program BitTest;
{$APPTYPE CONSOLE}

type
  TBits8 = packed set of 0..7;

var
  P, Q, V: TBits8;
  B: Byte;
begin
  P := [7, 6, 4, 2, 0];     (* 11010101 *)
  Q := [7, 6, 5, 3, 1];     (* 11101010 *)

  (* NOT P *)
  V := [0..7] - P;          (* 00101010 *)
  Writeln(Byte(V));         (* 42 *)

  (* P OR Q *)
  V := P + Q;               (* 11111111 *)
  Writeln(Byte(V));         (* 255 *)

  (* P AND Q  *)
  V := P * Q;               (* 11000000 *)
  Writeln(Byte(V));         (* 192 *)

  (* P XOR Q *)
  V := (P * ([0..7] - Q)) +
       (([0..7] - P) * Q);  (* 00111111 *)
  Writeln(Byte(V));         (* 63 *)
end.

列挙型 や 絶対変数 (absolute) と組み合わせる事もできます。

BitTest2.dpr
program BitTest2;
{$APPTYPE CONSOLE}

uses
  System.SysUtils;

type
  TBits8 = (b0, b1, b2, b3, b4, b5, b6, b7);
var
  Bits8: set of TBits8;
  ByteData: byte absolute Bits8;
begin
  Bits8 := [b7, b0];                    // 10000001
  Writeln('0x', IntToHex(ByteData, 2)); // 0x81
  Include(Bits8, b3);                   // 10001001
  Bits8 := Bits8 + [b4];                // 10011001
  Writeln('0x', IntToHex(ByteData, 2)); // 0x99 
end.

See also:

(8.2.5.) 集合定数とグローバル集合変数の初期化

Delphi では次のような集合定数が使えます。

SetsConstantsTest.pas
program ArrayConstantsTest;
{$APPTYPE CONSOLE}

// グローバル集合定数
const
  MyCharSet1: set of AnsiChar = ['A', 'B'..'F'];

// グローバル集合変数と初期化
var
  MyCharSet2: set of AnsiChar = ['A', 'B'..'F'];

  procedure Sub;
//var
//  ローカル集合変数は初期化できない
//  MyCharSet3: set of AnsiChar = ['A', 'B'..'F'];
  begin
    ...
  end; { Sub }
begin
  ...
end.

8.3. プログラムの開発について (On Program Development)

章構成を参考にした "PASCAL 原書第 4 版 (ISBN: 4563014664)" のこの節では、集合を用いたエラトステネスのふるいが 3 つ紹介されています。

Program 動作 説明
Prime1 × エラトステネスのふるい
Prime2 × 奇数だけの集合を使った
エラトステネスのふるい
Prime3 〇 奇数だけの集合を使った
エラトステネスのふるい

Prime1 と Prime2 が動作しないのは、

const
  N = 10000;
type
  Positive = 1..MaxInt;
var
  Sieve, Primes: set of 2..N;
  NextPrime, Multiple: Positive;

このような、10,000 個の要素が使える集合型を持つ Pascal という有り得ない想定の下で書かれた疑似コードだからです...ひょっとしたら世の中にはそんな Pascal があるのかもしれませんけれど。

せっかくなので、ちゃんと動作する Prime3 のコードを転載しておきます。

Prime3.pas
program Prime3(Output);
{ プログラム 8.5 - 3..10000の範囲内で、奇数だけを含むふるい
                  を使って素数を求める。 }
const
  SetSize = 128 { 処理系依存; >= 2 };
  MaxElement = 127 { SetSize - 1 };
  SetParts = 39 { = 10000 div Setsize div 2 };

type
  Natural = 0..MaxInt;

var
  Sieve, Primes:
    array [0..SetParts] of
      set of 0..MaxElement;
  NextPrime:
    record
      Part: 0..SetParts;
      Element: 0..MaxElement
    end;
  Multiple, NewPrime: Natural;
  P, N, Count: Natural;
  Empty: Boolean;

begin { 初期設定 }
  for P := 0 to SetParts do
    begin
      Sieve[P] := [0..MaxElement];
      Primes[P] := []
    end;
  Sieve[0] := Sieve[0] - [0];
  Empty := False;
  NextPrime.Part := 0;
  NextPrime.Element := 1;
  with NextPrime do
    repeat { 次の素数を求める }
      while not(Element in Sieve[Part]) do
        Element := Succ(Element);
      Primes[Part] := Primes[Part] + [Element];
      NewPrime := 2 * Element + 1;
      Multiple := Element;
      P := Part;
      while P <= SetParts do { 除去 }
        begin
          Sieve[P] := Sieve[P] - [Multiple];
          P := P + Part * 2;
          Multiple := Multiple + NewPrime;
          while Multiple > MaxElement do
            begin
              P := P + 1;
              Multiple := Multiple + SetSize;
            end
        end;
      if Sieve[Part] = [] then
        begin
          Empty := True;
          Element := 0
        end;
      while Empty and (Part < SetParts) do
        begin
          Part := Part + 1;
          Empty := Sieve[Part] = []
        end
      until Empty;
      Count := 0;
      for P := 0 to SetParts do
        for N := 0 to MaxElement do
          if N in Primes[P] then
            begin
              Write(Output, 2 * N + 1 + P * SetSize * 2:6);
              Count := Count + 1;
              if (Count mod 8) = 0 then
                Writeln(Output)
            end
end.

このコードは割と真面目な "エラトステネスのふるい" なので、0～10000 (正確には 0～9983) から素数を見つけるには相当時間が掛かります。ひょっとするとメモリ不足で実行できないかもしれません。

const
  SetSize = 256;
  MaxElement = 255;
  SetParts = 0;

このような設定にすると (環境依存ですが) 0～511 の範囲の素数を探します。

See also:

(8.3.1. ) Unicode 版 Delphi と CharInSet() 関数

Char 型のサイズは環境依存です。標準 Pascal では Char 型が 8 ビット以下である前提のサンプルコードがあり、この集合型は最たるものです。

バージョン 2009 以降、Delphi は 文字列型 / 文字型を Unicode に移行しました。内部で使われている符号化形式は Windows に合わせて UTF-16LE となっています。つまり、文字の 1 要素のサイズが 16 ビットになりました。これに伴い、Char 型も 16 ビットの WideChar と同じになりました。

そうなると困るのが集合型と共によく使われる in 演算子です。集合型の基底型は

  • 要素数は 256 個以内
  • 要素の値は 255 を超えてはいけない

という事でした。例えば次のようなコードがあったとします。

var
  MyCharSet: set of Char;
  c: Char;
begin
  MyCharSet := ['0'..'9', '*', '#'];
  c := '7';
  if c in MyCharSet then
    Writeln('OK!');
end.

ANSI 版 Delphi の Char 型は AnsiChar (8 ビット) なので何の問題もありません。

  MyCharSet: set of Char;

しかしながら Unicode 版 Delphi の Char 型は UnicodeChar (16 ビット) なので集合型の基底値には使えません。正確に言うと使えるには使えるのですが、範囲が 0x0000～0x00FF までに制限されます。

Unicode 版 Delphi で 8 ビットの Char (AnsiChar) を使ったコードは次の通りです。

var
  MyCharSet: set of AnsiChar;
  c: AnsiChar;
begin
  MyCharSet := ['0'..'9', '*', '#'];
  c := '7';
  if c in MyCharSet then
    Writeln('OK!');
end.

このコードには問題がある可能性があります。このロジックが文字を判定するものだったとしたらどうでしょうか？文字列が ANSI から Unocode に変わっても文字を判断しなければならないとしたら？

それでも多くの場合、処理している文字が ASCII 7 ビットの範囲内であれば、処理は正しく行われます。W1050 のワーニングが出ますが、これは CharInSet() 関数を使う事で回避できます。

例えば次のようなコードは

program CharInSetTest;
{$APPTYPE Console}
var
  c: Char;
begin
  c := '7';
  if c in ['0'..'9', '*', '#'] then
    Writeln('OK!');
end.

このように変更できます。

program CharInSetTest;
{$APPTYPE Console}

uses
  System.SysUtils;

var
  c: Char;
begin
  c := '7';
  if CharInSet(c, ['0'..'9', '*', '#']) then
    Writeln('OK!');
end.

CharInSet() は組み込みルーチンではないので、System.SysUtils を uses 句に追加する必要があります。

See also:

(8.3.2. ) Pascal の字下げ (インデント) スタイル

この節は完全に余談です。

J&W (第 4 版) のサンプルコードのインデントスタイルは一貫しており、C 言語で言うところの GNU スタイルで書かれています。J&W スタイルとでも名付けましょうか。

 while (x = y) do
   begin
     something;
     somethingelse;
   end;
 finalthing;

これに対し、Borland 系の Pascal (Turbo Pascal, Borland Pascal, Delphi) は Borland スタイルで書かれています。これは C 言語で言うところの BSD/オールマンのスタイルです。

 while (x = y) do
 begin
   something;
   somethingelse;
 end;
 finalthing;

Wikipedia の BSD/オールマンのスタイル の項には

これはPascalやTransact-SQLの標準的な字下げに似ていて、

と書かれていますが、Pascal としては J&W スタイル と Borland スタイルのどちらが標準的なのかは意見が分かれる所だろうと思います。ただ、現在の Pascal コードで圧倒的に目にする事が多いのは Borland スタイルです。Delphi のソースコードを読む上でも Borland スタイルに慣れておいたほうがいいと思います。

Delphi でソースコードの整形は〔Ctrl〕+〔D〕またはコードエディタのコンテキストメニューから行えます。デフォルトは当然 Borland スタイルです。

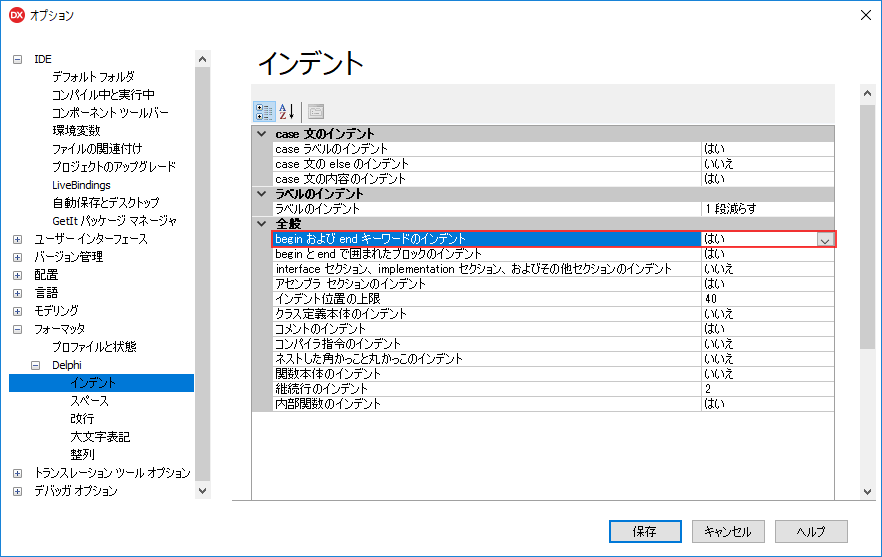
ソースコードを J&W スタイルで整形したい場合には [ツール | オプション] の [フォーマッタ | Delphi | インデント] で begin および end キーワードのインデント を "はい" に設定します。
image.png
C# のコーディング規則が BSD/オールマンのスタイルに則っているのは...察してください。

See also:

索引

[ ← 7. レコード型 ] [ ↑ 目次へ ] [ → 9. ファイル型 ] :sushi:

7
2
3

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
7
2

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?