はじめに

Twitterをやっていると無限に飯テロ画像が流れてきます。対抗して飯テロ画像を生成して流せばよいと思ったのでそういうの作りました。記事中では WGAN およびその改良手法である WGANgp について説明しています。

WGANについてはWasserstein GAN
WGANgpについてはImproved Training of Wasserstein GANs

詳しい内容については論文を読みましょう。

DCGAN の問題点

効果的な飯テロを行うには画像の解像度は高い方がよいですが、高解像度の画像を DCGAN で作るのは難しいです。GAN の問題点についてはFrom GAN to WGANが詳しいので読むことをオススメします。簡単に列挙すると以下の問題があります。

discriminator と generator をナッシュ均衡に到達させることが難しい
低次元多様体上にある 2 つの分布 $p_r$ と $p_g$ が (特に学習初期において) 互いに素になりがちであり、分布間の距離として JS divergence を用いるとほぼ意味をなさない
2 番のような条件下では discriminator の勾配が消失するため学習がまともに進まない
2 番、3 番の条件によって、たまたま discriminator を騙しやすい fake sample を生成できると generator はあらゆる入力からその fake sample を生成しようとし始める (mode collapse)

これらの問題に対処するために WGAN が考案されています。

Wasserstein 距離と WGAN

Wasserstein 距離 (Wasserstein Distance) $W(p_r, p_g)$ は一方の分布 $p_r$ から他方の分布 $p_g$ への最少移動コストです。イメージとしてはある形に盛られた土を別の形にするために必要な土の輸送コスト (ある地点xから別の地点yに動かす土の量) × (地点xと地点yの距離) の総和の最小値を考えるとイメージしやすいと思います。このイメージから、別名で Earth Mover's Distance とも呼ばれます。式は以下の通り。

$$W(p_r, p_g) = \inf_{\gamma \sim \Pi(p_r, p_g)} \mathbb{E}_{(x, y) \sim \gamma}[||x-y||]$$

$\gamma \sim \Pi(p_r, p_g)$ は $p_r$ から $p_g$ に至るための 1 つの移動プランを示します (同じ 2 個の分布に対して可能な輸送パターンは沢山ある) 。$\gamma$ 自身も確率密度関数なので、結局求めるべき $W(p_r, p_g)$ は 2地点の距離 $||x-y||$ の $\gamma$ の下での平均の下限ということになります。

Wasserstein 距離を GAN の損失関数として使う

$\inf_{\gamma \sim \Pi(p_r, p_g)}$ を計算するために一々 $\Pi(p_r, p_g)$ に含まれるすべての同時分布について計算するのはあまりにもしんどいです。そこで著者たちは、Kantorovich-Rubinstein 双対性から以下のように式を変形しています。

$$W(p_r, p_g) = \frac{1}{K} \sup_{||f||_L \leq K} \mathbb{E}_{x \sim p_r} [f(x)] - \mathbb{E}_{x \sim p_g} [f(x)]$$

$f$ は K-リプシッツ連続である必要があります。

WGAN において discriminator はより正しく Wasserstein 距離を測れるような $f_w$ を見つけるために $w$ を学習します。そして (generatorにとっての) 損失関数は $p_r$ と $p_g$ の間の Wasserstein 距離から構成されます。結果として以下の最小化問題を解くことになります。

$$
L(p_r, p_g)=W(p_r, p_g)=\min_{w \in W} \mathbb{E}_{z \sim p_r(z)}[f_w(g_\theta(z))] - \mathbb{E}_{x \sim p_r}[f_w(x)]
$$

Kantorovich-Rubinstein 双対性を使ってどうやって Wasserstein 距離を求める式を変形するのか知りたい人はWasserstein GAN and the Kantorovich-Rubinstein Dualityを読んでください僕は読んでいません。

discriminator は直接的に fake samples と real samples を分けるのではなく、代わりに Wasserstein 距離を正しく測定するためのリプシッツ連続な関数を構成しようとします。学習中損失関数の値が減少するにつれて Wasserstein 距離は小さくなり、generator が真のサンプルの分布に近い出力を出すようになっています。

大きな問題の 1 つは $f_w$ のリプシッツ連続性をどのように維持するかということですが、WGAN の論文中では $w$ を $[-0.01, 0.01]$ の範囲にクリッピングしています。その結果 $w$ は小さなパラメータ空間 $W$ に留まることになるため、$f_w$ は上界と下界を持ちリプシッツ連続性が保持されます。

擬似コード

WGANgp

WGAN の問題点はクリッピングという非常に胡散臭い方法でリプシッツ連続性を保証しようとする点です。実際、上述のようなクリッピングを行えば多くのパラメータは $0.01$ か $-0.01$ に張り付いてしまうでしょう。しかし、そもそもどういう制約をかければよいのかという問題が結構難しいです。

WGAN の改良手法として提案された WGANgp では以下の式により discriminator を最適化します。

$$
L = \min_{w \in W}\mathbb{E}_{\tilde{x} \sim p_g}[f_w(\tilde{x})] - \mathbb{E}_{x \sim p_r}[f_w(x)] + \lambda\mathbb{E}_{\hat{x} \sim p_{\hat{x}}}[(||\nabla_{\hat{x}}f_w(x)||_2 - 1)^2]
$$

ただし、$\hat{x}$ は $\hat{x}=\epsilon\tilde{x} + (1 - \epsilon)x, \epsilon \sim U[0, 1]$ です。真のサンプルと偽のサンプルの間の線分上の点を取っていることになります。

WGAN の場合に比べて3つ目の項 $ + \lambda\mathbb{E}_{\hat{x} \sim p_{\hat{x}}}[(||\nabla_{\hat{x}}f_w(x)||_2 - 1)^2] $ が増えています。これは$f_w$ の $\hat{x}$ についてのヤコビ行列の L2 ノルムの平均が 1 となるような制約をかけることを意味しています。勾配に対して損失を設けている (gradient penalty) ことが WGANgp という名前の由来です。

これがなぜリプシッツ連続性を保証するための制約として働くのかについては気が向いたら別の記事でまとめます。

疑似コード (赤枠が WGAN からの変更点)

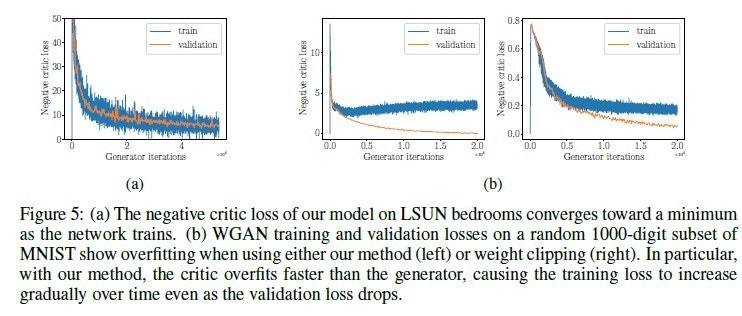
WGAN の枠組みでは discriminator が generator よりも早く過学習するため、training data の loss が上がり始めているにも関わらず validation data に対する loss は下がり続けているというようなことが起きます。学習の進行具合を見ながら学習させたい場合には必ず validation data を用意しておきましょう。