画像のスタイル変換とかがやりたいので関連する論文を読んでいます。
Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks
実際に試してみた話はこちら。
問題設定
$x \in X, y \in Y$ について $ G:X \rightarrow Y $ となるような $G$ を構成したい。画像について言えばこれは image-to-image translationを意味していて、白黒画像への着色やセグメンテーションなどを含む。
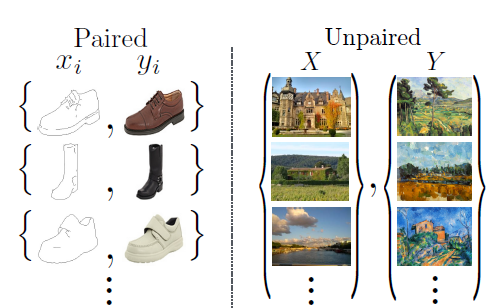
こういった問題の場合、通常はタスク設計として ${x_i, y_i}$ の組を沢山用意しておいて学習に用いるという方法が考えられる、しかし、現実的に対になるような ${x_i, y_i}$ を用意することが困難であるケースも存在するので、対になるデータのセットを使わずになんとかドメイン $X$ からドメイン $Y$ への image-to-image translation を行いたい。
提案手法
GAN を使って $G:X \rightarrow Y$ となる $G$ について、$\hat{y} = G(x), x \in X$ なる $\hat{y}$ が $y \in Y$ と discliminator によって区別されないようにできればいい。ただし、もし仮にこの点については理想的な $G$ が $G:X \rightarrow Y',Y' = Y$ となるとしても、個々の $x, y'$ についてそれが意味のある対になりうる保証はない。
($S \subset X$ について $G(x) = y, x \in S$ みたいなことされると意味がないという意味だと思う。mode collapse と同じ)
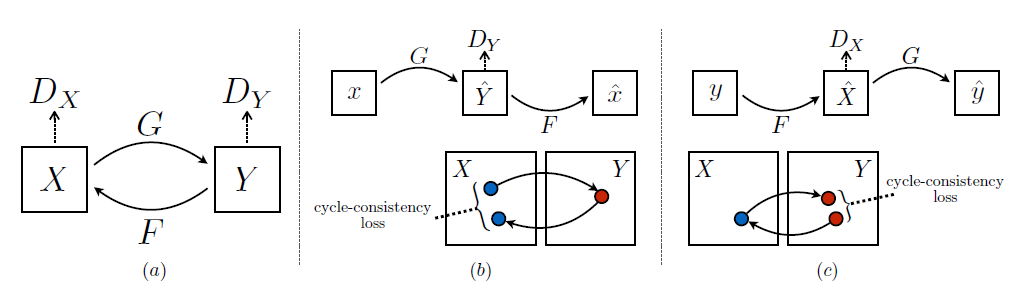
これを解決するため、cycle consistent を導入した。
$G:X \rightarrow Y, F:Y \rightarrow X$ である $G, F$ について、$F(G(x)) \fallingdotseq x, G(F(y)) \fallingdotseq y$ となっていればよいという考え。
定式化
2 つのドメイン $X$ および $Y$ について、訓練データとして{$x_1, x_2,\dots,x_N|x_i \in X$}、{$y_1, y_2, \dots, y_M|y_i \in Y$}があり$x \sim p_{data}(x),y \sim p_{data}(y)$ とする。また、2 つのドメイン間のマッピングを行う関数として $G:X \rightarrow Y, F:Y \rightarrow X$ 、それぞれのドメインに対応する discriminator $D_X, D_Y$ を用意する ($D_X$ は $x$ と $F(y)$ を見分ける。$D_Y$ は $y$ と $G(x)$ を見分ける)。
Adversarial Loss
ここは DCGAN と同じ。
$G$ と $D_Y$ について、
\mathcal{L}_{GAN}(G, D_Y, X, Y) = \mathbb{E}_{y \sim p_{data}(y)}[ \log{D_Y(y)}] + \mathbb{E}_{x \sim p_{data}(x)}[\log{1-D_Y(G(x))}]
$$\min_{G}\max_{D_Y}\mathcal{L}_{GAN}(G, D_Y, X, Y)$$
$F$ と $D_X$ について、
\mathcal{L}_{GAN}(F, D_X, Y, X)
= \mathbb{E}_{x \sim p_{data}(x)}[ \log{D_X(x)}] + \mathbb{E}_{y \sim p_{data}(y)}[\log{1-D_X(F(y))}]
$$\min_{F}\max_{D_X}\mathcal{L}_{GAN}(F, D_X, X, Y)$$
Cycle Consistency Loss
こっちが肝。
$F(G(x)) \fallingdotseq x, G(F(y)) \fallingdotseq y$ に向かうような損失を考える。
\mathcal{L}_{cyc}(G, F) = \mathbb{E}_{x \sim p_{data}(x)}||F(G(x)) - x||_1 + \mathbb{E}_{y \sim p_{data}(y)}||G(F(y)) - y||_1
の形で $F(G(x))$ と$x$、$G(F(y))$と$y$の間のL1ノルムを取ることで実現する。なぜL1ノルムなのかは書いていない。
また、この部分の損失の計算にも Adversarial Loss を適用することも試したが特に改善はしなかったと書いてある。
$G \circ F$ と $F \circ G$ は共に autoencoder として働くことになる。
Full Objective
これらを踏まえて、最終的な損失関数は以下のようになる。$\lambda$ はAdversarial Loss と Cycle Consistensy Loss のバランスを決めるハイパーパラメータ。論文中では$\lambda=10$を使用している。
\mathcal{L}(G, F, D_X, D_Y) = \mathcal{L}_{GAN}(G, D_Y, X, Y) + \mathcal{L}_{GAN}(F, D_X, Y, X) + \lambda \mathcal{L}_{cyc}(G, F)\\
G^*,F^*=\arg\min_{G,F}\max_{D_X,D_Y}\mathcal{L}(G, F, D_X, D_Y)
を解くことになる。
実験
Limitation and Discussion
CycleGAN が上手くいかなかった例として以下のケースを挙げている。
- 色やテクスチャの変換については概ね上手くいくものの、形を変化させるような変換はほとんど上手くいかない。これは Cycle Consistency Loss のために入力画像に対して最小限の変化だけでドメインを変えるよう試みるため。
- データセットの分布による失敗。上図右の例では、Horse と Zebra のデータに人が乗馬しているような画像が無かったために変な変換をしてしまっている。
- 写真と絵を変換する際、木を建物に変えてしまうなどの失敗が見られた。これに対しては弱いセマンティクスの情報 (?) を与えることで解決できる可能性がある (weak semantic supervision)