Thresholdモデル
その2でちらっと触れましたが、今回はThresholdモデルを紹介していきます。「Financial risk modelling and portfolio optimization with R」で指摘されていますが、Block maximaやr-block maximaを使ってファイナンスのデータを扱う場合、以下の問題点が指摘されています。
- 金融商品によっては長期間のデータが確保しずらい(10年、20年超等)。サンプル数が少ないと標準誤差が大きくなってしまい、パラメータ値の信頼区間が広めに推定されてしまう。
- 極値分布を推定する際、極値(最大値、最小値)のすべてが極値として扱われる必要はない。
ということで登場するのがThresholdモデルです。ではある閾値($u$)を設定し、それを超える値を極値(閾値超過データ)として、サンプル抽出し、分布を推定します。
一般化パレート分布
この際に当てはめる分布は一般化極値分布ではなく、一般化パレート分布になります。一般化パレート分布はGP($\sigma, \xi$)で表され、次の式になります。
$$
H(y)=1-(1+\xi \frac{y}{\sigma})^{-1/\xi}
$$
パラメーターは2つで、スケールを示す$\sigma$(sigma)、形状を示す$\xi$(xi)となります。この形状パラメーターは一般化極値分布と同じで、$\xi>0$のときには超過損失の上限があり、$\xi<0$のときには超過損失の上限がないということになります。そして$\xi\rightarrow0$でリミットを取るときは
$$
H(y)=1-exp(-\frac{y}{\sigma})
$$
と標記でき、パラメーターが$-\frac{1}{\sigma}$の指数分布になります。次のグラフは一般パレート分布の確率密度関数で、$\sigma$=1とし、$\xi$を色々変えてプロットしたものです。

データ
さて、実際にRを使ってThresholdモデルを使っていきたいと思います。今回使用するデータはismevにあるdowjonesです。1995年09月11日から2000年09月07日までのDow Jones Indexの終値になります。
library(ismev)
data("dowjones")
str(dowjones)
'data.frame': 1304 obs. of 2 variables:
$ Date : POSIXt, format: "1995-09-11 01:00:00" "1995-09-12 01:00:00" ...
$ Index: num 4705 4747 4766 4802 4798 ...
日付
極値分析にはいらないのですが、グラフが見やすくなるので、dowjonesに格納されている日付データをPOISXct形式で取り出しておきます。
library(lubridate)
dates <- parse_date_time(x = dowjones$Date, orders ="Y-m-d H:M:S")
終値
price <- dowjones$Index
plot(x=dates, y=price, t="l")

ログリータン
ログリータンを計算。100をかけてパーセント標記にしています。
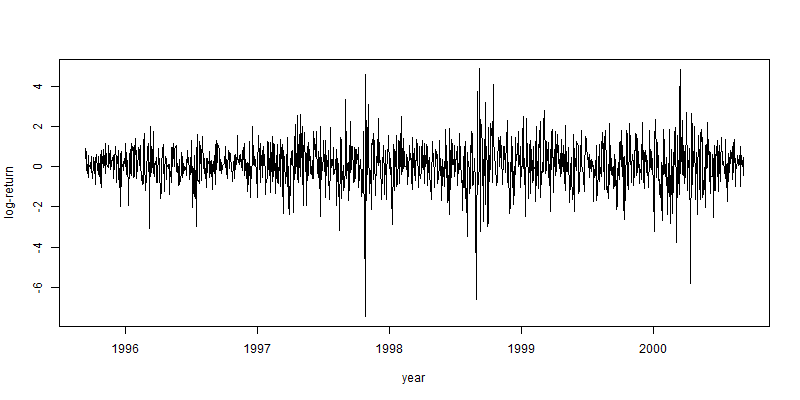
ret <- diff(log(price))*100
plot(x=dates[-1], y=ret, t="l", xlab="year", ylab="log-return")
損失
今回はリスク管理という観点から、どれだけ大きな損失が発生するかを見ていきたいので、ログリータンをプラスの損失に変換します。
loss <- -1*ret
plot(x=dates[-1], y=loss, t="l", xlab="year", ylab="log-return")

閾値の設定
Mean Residual Life Plot
Thresholdモデルで重要なのが閾値をどのように選ぶかという点です。閾値が高すぎるとサンプル数が減ってしまい、標準誤差が大きくなってしまいますが、逆に低すぎるとモデルのバイアスが高くなってしまうというトレードオフの関係があります。ただ、慣例としてはできるだけ低く設定し、サンプル数を増やすということが行われています。
閾値の設定でよく用いられるのはMean Residual Life Plotを用いた方法です。ismevのmrl.plotを使えば一発でグラフが表示されますが、まずはそれを用いない方法で何が行われているかを確認したいと思います。
下記がMean Residual Life Plotを表示するためのコードです。1行目で候補となる閾値を選択。ここではlossの最小値から最大値の範囲で0.01刻みで、閾値を設定しています。2行目は結果を格納するベクトルです。まずはすべてゼロにし、後で更新していくようにしています。そしてforループでそれぞれの閾値ごとに、超過するサンプルの抽出を行い、そのサンプルの超過した分だけの値のみを平均にし、先ほど作ったベクトルに格納していきます。最後にプロットします。
u <- seq(min(loss) , max(loss), 0.01)
mean.excess <- vector("numeric", length(u))
for(i in 1:length(mean.excess)){
threshold.exceedances <- ret[ret > u[i]]
mean.excess[i] <- mean(threshold.exceedances - u[i])
}
plot(x=u, y=mean.excess, t="l")

ismevのmrl.plotを使うとこちら。95パーセンタイルも分かります。
library(ismev)
mrl.plot(loss)

このグラフの解釈の仕方ですが、綺麗な線形状になっていて、95パーセンタイルの幅がそこまで広くなりすぎていないところを選択します。ここでは2を閾値として選択したいと思います。かなり主観的ではありますが…、色んな文献で指摘されています…。
他の方法
「An Introduction to Statistical Modeling of Extreme Values」で言われている別の方法が、何種類かの閾値を用いてGPD推定を行い、パラメーターの標準誤差を比較し、比較的標準誤差の低い中で、最大の閾値を用いたモデルを選択するというものです。ここでは上記のMRLを踏まえて、0~3の閾値を用いて、二つのパラメータとその95パーセンタイルを求めます。
gpd.fitrange(ret, umin = 0, umax = 3, nint = 31)
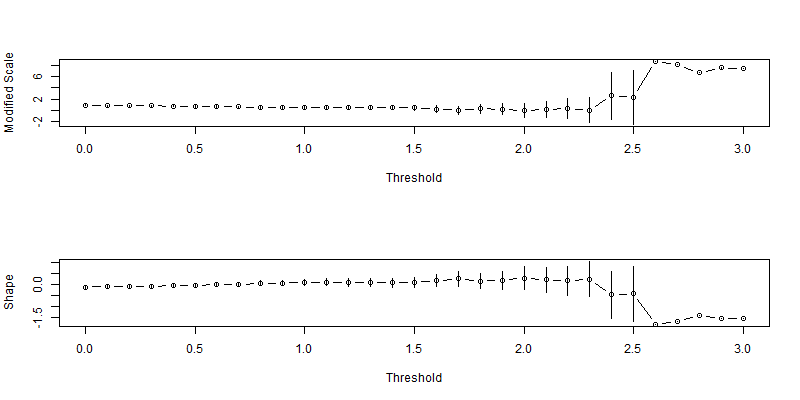
やはり閾値2を超えるあたりから標準誤差が大きくなっているので、2を閾値として選びたいと思います。
閾値のまとめ
閾値を超えるサンプル数は42となりました。これは全体1303のうち、およそ3%となっています。この3%はExceedance rateと呼ばれます。
# number of exceedance
num.exc <- length(loss[loss > 2])
num.exc
[1] 42
# number of complete sample
num.all <- length(loss)
num.all
[1] 1303
# exceedance prob
ex.prob <- len.sam/len.com
ex.prob
[1] 0.03223331
プロット
プロットして確認したのが、こちらです。
col.exceed <- loss
col.exceed[col.exceed > 2] <- "red"
col.exceed[col.exceed <= 2] <- "black"
plot(x= dates[-1], y=loss, pch=20,
xlab="Year", ylab="Loss of Dow Jones 30", col=col.exceed)
abline(h=2)

GPDへの当てはめ
ismevのgpd.fitを使って当てはめを行っていきます。
fitgpd <- gpd.fit(loss, threshold = 2)
$threshold
[1] 2
$nexc
[1] 42
$conv
[1] 0
$nllh
[1] 34.16881
$mle
[1] 0.6181962 0.2943859
$rate
[1] 0.03223331
$se
[1] 0.1496050 0.1919394
パラメーターの検証
信頼区間
前回に引き続き、同じ手法で95%信頼区間を計算します。またしても、形状パラメーターがゼロをまたいでしまっています…。
low <- fitgpd$mle - 1.96*fitgpd$se
upper <- fitgpd$mle + 1.96*fitgpd$se
data.frame(low=low, upper=upper, row.names = c("sigma", "xi"))
| lower | upper | |
|---|---|---|
| sigma | 0.32497037 | 0.9114220 |
| xi | -0.08181527 | 0.6705872 |
プロファイル尤度
ということでextRemesを使って、$\xi$のプロファイル尤度を見てみると、ギリギリゼロをまたいでいないので、一応$\xi$はゼロではないと言えます。
library(extRemes)
fitgpd2 <- fevd(loss, threshold = 2, type = "GP")
ci.fevd(fitgpd2, type = "parameter", which.par = 2, method = "proflik")
[1] "Profile Likelihood"
[1] "shape: 0.294"
[1] "95% Confidence Interval: (0.0073, 0.7859)"
再現レベル
推定された分布から、損失額の再現レベルが分かります。約10%の損失が10年に一度、約20%の損失が100年に一度起こるという推定結果になります。というか、二つのグラフとも右のすそ野の広がり方が尋常じゃないですね…。
ここでは100年に一度を再現してみましたが、100年に一度といえばリーマンショックの際によく使われた言葉です。1995年09月11日から2000年09月07日までのでデータを基にした分布約20%が最もらしい再現レベルだと伝えてくれています。2008年のダウ平均株価下落率を見てみると7~8%前後でしたので、今回のモデルはあまり精度が良くないということになるんでしょうか?いやいや、リーマンショックは100年に一度のレベルじゃないという見方も可能だと思います。というのも、1987年のブラックマンデーの際のダウ平均の下落率は約22%。モデルは良いところをついているようにも思えます。
gpd.prof(fitgpd, m = 10, xlow = 5, xup = 50)
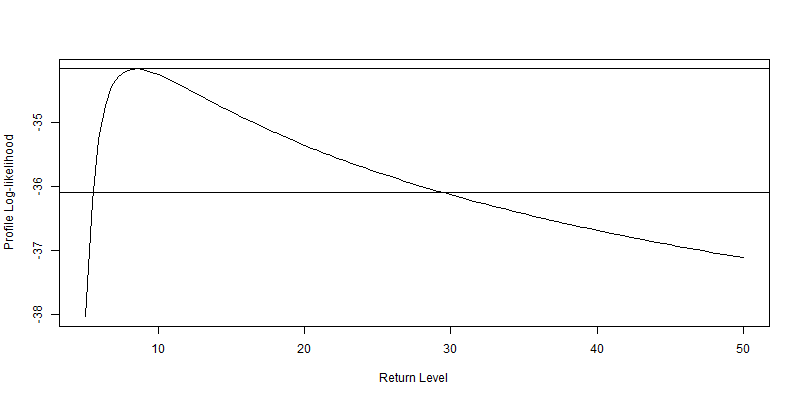
gpd.prof(fitgpd, m = 100, xlow = 7, xup = 200, nint = 1000)
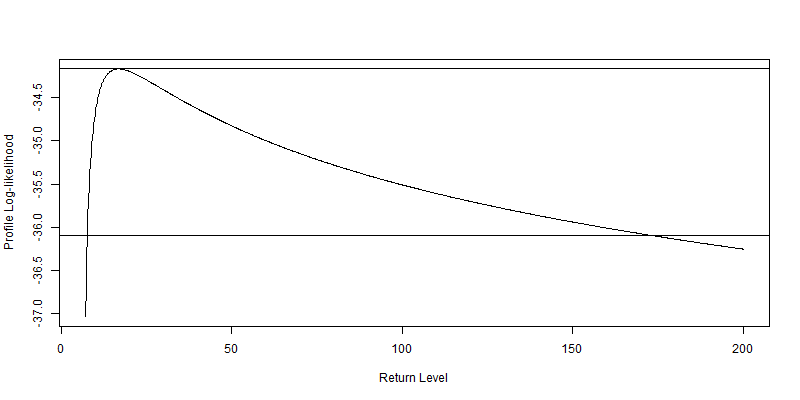
モデルの検証
最後にモデルの検証を行っていきます。
gpd.diag(fitgpd)
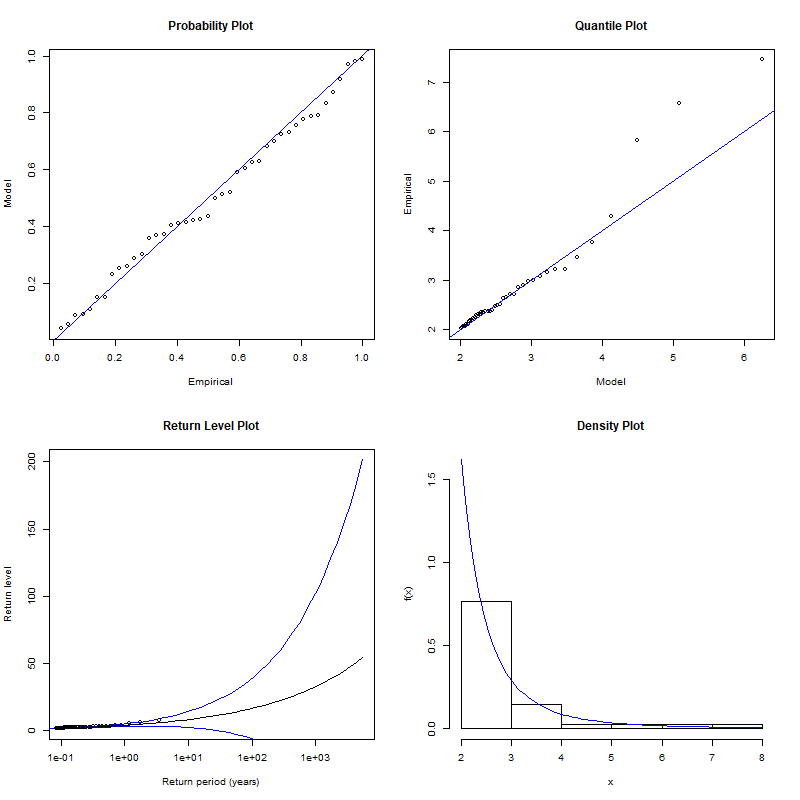
PPプロットとReturn Levelは概ね一致していますが、qqプロットは右のすそ野をうまく説明できていません。
さて、最後の最後に超過データのグラフを見てみたいのですが、今回採用された42のサンプルは一定の期間で固まって発生しています。2000年の後のドットコムバブル崩壊後が顕著ですね。これは互いに独立であるという点を満たしていないのではないかという疑いが非常に濃厚で、Thresholdモデルを使った際の短所になります。次回以降でこの点を克服するDeclusteringという手法を紹介していきたいと思います。


