今回はc言語を用いて、project eulerの10問目を解いていきます。
内容は「200万以下の素数の和を求める」というもの。
素数判定の一番単純な方法は以下のようになります。
素数判定する数をnとすると、nをn未満の数で割り、割り切れるものがなければその数は素数と判定するもの。(以下コード)
int i;
int flag=0;
for(i=2; i<n; i++){
//nがiで割り切れるならflag=1とする
if(n%i==0) flag=1;
}
if(flag==0) printf("素数");
else printf("素数ではない");
n=√n*√n なので、iは2...√nとして高速化することもできます。
しかし、今回の問題では0から200万の素数判定を行わなければいけないので、この方法では時間がかかりすぎてしまう...
そこで今回は、動的計画法を用いて問題を解いていきます。
(エラトステネスの篩というらしいです。エラトステネスの篩は簡単なアルゴリズムなのですが、自分の力不足のため、複雑なものになっています)
アルゴリズムは以下の通り。
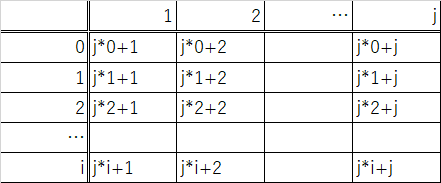
表の縦軸をi、横軸をjとし、各マスに対応する数字をj*i+jと定めていきます。
抽象的でよくわからないので...
Ex.)
i<=3、j<=4とすると、表と各マスに対応する数字は以下のようになります。
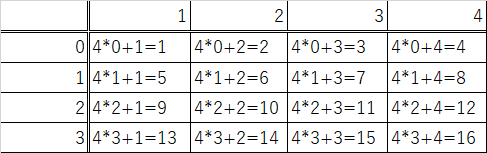
見てわかるように、各マスに対応する数字が0~16(=(3+1)*4)まで順番に並んでいます。
このような表を使用して、動的計画法を用いた、ある数以下の素数判定を行います。
例の表を使用して、16以下の素数を判定していきます。
まず以下のように表の各マスの値をすべて0に初期化します。
各マスに入る値は0または1であり、0は素数、1は非素数に対応します。
(1~16という数字は各マスに対応する数字であり、各マスの値とは無関係です。)

左の表はマスに対応する数字、右の表はマスの値を表しています。
ここから、数字の小さい順に素数判定を行っていきます。
まず1は素数ではないので飛ばします(探索済みとする)。
次に2に注目します。すると2に対応するマスの値は0なので2は素数であるとわかります。
さらに2の倍数は素数ではないため、2の倍数に対応するマスの値を1と設定します。
このとき1としたマスに対応する数字は、割り切れる数字が存在するという意味で、素数ではないと判定されます。
その後2を探索済みとします。

このとき、探索済みのマスを黄色、探索中のマスを青、マスの値を変更した場所を赤にしています。
次に3に注目します。すると3に対応するマスの値は0なので3は素数です。
同様に3の倍数に対応するマスの値を1とします。

次に4に注目します。4に対応するマスの値は1なので4は素数ではないとわかります。
同様に4の倍数に対応するマスの値を1にします。(4は2の倍数なので、マスの値が変わる場所はありません。)
先ほども説明したように、n=√n*√nであるので、√nまで探索すればnまでの素数を導き出せます。
この場合は16以下の素数を求めているので、4まで探索すればすべての素数を導き出せます。
最終的に得られる表は以下のものになります。

緑色の部分が素数であるという結果が出ました。
このアルゴリズムを使用すると、先ほどのアルゴリズムよりかなり早く素数を導くことができます。
以下にコードを載せます。
表のつくり方が上記の方法と少し違います。
/*project euler10 を解くプログラム*/
/*200万以下の素数の和を求めるプログラム*/
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
#include<time.h>
int main(void){
int Upper=2000000;
int root_Upper = (int)sqrt(Upper)+1;
long long sum=0;
int **Table;
//動的メモリの確保
Table = malloc(sizeof(int *)*(root_Upper+1));
for(int i=0; i<root_Upper+1; i++){
Table[i] = malloc(sizeof(int)*root_Upper+1);
}
//Tableの初期化
for(int i=0; i<=root_Upper; i++){
for(int j=0; j<=root_Upper; j++){
Table[i][j] = 0;
}
}
//時間計測開始
clock_t time_start = clock();
//動的計画法の実行(マスの数字は J*i + j)
for(int i=0; i<=root_Upper; i++){
for(int j=0; j<root_Upper; j++){
if(root_Upper*i+j > Upper){
i=root_Upper;
break;
}
if(root_Upper*i+j>=2 && Table[i][j]==0){
sum += root_Upper*i+j;
if(root_Upper*i+j <= root_Upper){
for(int k=root_Upper*i+j; k<=Upper; k+=root_Upper*i+j){
Table[k/root_Upper][k%root_Upper] = 1;
}
}
}
}
}
//時間計測終了
clock_t time_end = clock();
//動的メモリの解放
for(int i=0; i<root_Upper+1; i++){
free(Table[i]);
}
free(Table);
printf("%d以下の素数の和: %lld\n", Upper, sum);
printf("実行時間: %fs\n", (double)(time_end-time_start)/CLOCKS_PER_SEC);
return 0;
}
実行結果:
2000000以下の素数の和: 142913828922
実行時間: 0.054000s
このコードの中では、配列の要素を20000にしているのですが、要素数20000だと大きすぎてプログラムが実行できなかったため、以下の部分でmalloc関数を用いてメモリの確保を行っています。
int **Table;
//動的メモリの確保
Table = malloc(sizeof(int *)*root_Upper);
for(int i=0; i<root_Upper; i++){
Table[i] = malloc(sizeof(int)*root_Upper);
}
malloc関数というのは、あらかじめメモリ領域を確保する関数です。このようにあらかじめメモリ領域を確保しておくことにより、配列の数がオーバーフローするということを防ぐことができます。
このプログラムでは時間を計測しています。今回のように求める数が200万程度であれば、実行時間は0秒であり、高速に実行できます。
こうして無事にProjectEulerの10問目を解くことができました!!よかった!!