時系列データの外れ値検出

トレンドを持った時系列データに対して外れ値の検出を行うために指数加重移動平均を使ったらけっこういい感じだったのでまとめる。

注意点として、今回の手法は「理論的に裏付けられている手法」でも「時系列解析で一般的に用いられる手法」でもない (と思う) ので、真似する際は自己責任で。

他にも、「外れ値検出 ⊂ 異常検知」と考えると以下のような手法もあるので参考までに。
Pythonによる時系列データの異常検知 - Technology Topics by Brains

環境

今回は Python 3.6 環境で、以下のモジュールを利用する。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

また、Jupyter Notebook 上でグラフを表示させるために以下の設定をしている。

%matplotlib inline

データ

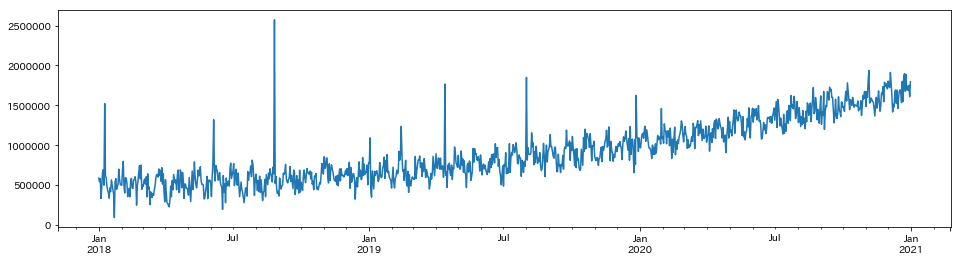
今回はテキトーな時系列データを生成してそれを使うことにする。

# 乱数を固定
rand = np.random.RandomState(seed=20)

# データを生成
idx = pd.date_range(start='2018-01-01', end='2020-12-31', freq='D')
x = np.arange(len(idx))
y = 500000 \
    + x ** 2 \
    + np.sin(x/4) * 100000 \
    + rand.randn(len(x)) * 100000 \
    + rand.gamma(0.01, 1000000, len(x))

# Series に変換
ts = pd.Series(y, index=idx)

# 描画
ts.plot()

トレンド + 周期 + ノイズ の中に外れ値のようなものがいくつか見受けられると思う。

この外れ値を検出したい。

指数加重移動平均

指数加重移動平均 (Exponential Weighted Moving Average) は、直近のデータを重視し古いデータになるほど指数関数的に重みが減少する移動平均の一種。

単純移動平均と比べると古いデータに影響されにくいので、急激にトレンドが変化する時系列データでも適用しやすい。

Pandas では ewm メソッドを使うことで簡単に指数加重移動平均を計算できる。

ewm_mean = ts.ewm(span=90).mean()  # 指数加重移動平均

fig, ax = plt.subplots()
ax.plot(ts, label='original')
ax.plot(ewm_mean, label='ewma')
ax.legend()

おおまかなトレンドが掴めていることがわかると思う。

この移動平均から大きく外れたデータを外れ値として扱いたい。

偏差から外れ値を検出する

移動平均と同様に ewm メソッドを用いて移動標準偏差を求め、「その時点でのデータのバラつき具合」の指標として利用する。

def plot_outlier(ts, ewm_span=90, threshold=3.0):
    assert type(ts) == pd.Series
    fig, ax = plt.subplots()

    ewm_mean = ts.ewm(span=ewm_span).mean()  # 指数加重移動平均
    ewm_std = ts.ewm(span=ewm_span).std()  # 指数加重移動標準偏差
    ax.plot(ts, label='original')
    ax.plot(ewm_mean, label='ewma')

    # 標準偏差から 3.0 倍以上外れているデータを外れ値としてプロットする
    ax.fill_between(ts.index,
                    ewm_mean - ewm_std * threshold,
                    ewm_mean + ewm_std * threshold,
                    alpha=0.2)
    outlier = ts[(ts - ewm_mean).abs() > ewm_std * threshold]
    ax.scatter(outlier.index, outlier, label='outlier')

    ax.legend()
    return fig


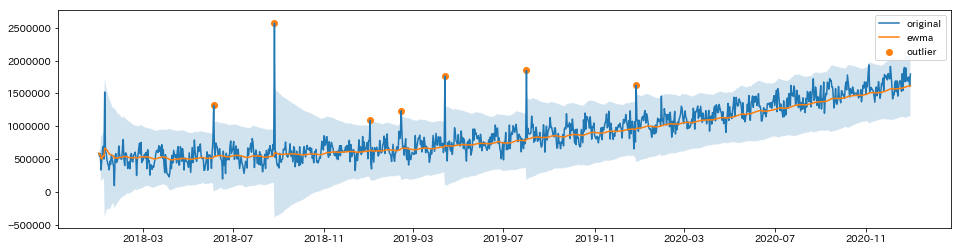
plot_outlier(ts)

オレンジの ◯ が外れ値として検出されたデータで、直感的にもそれほど間違ってはいないと思う。

最初 (2018-01 あたり) にある外れ値が検出できていないが、これは移動標準偏差を計算するための過去のデータが足りないためで、過去のデータのみからこれを検出するのは難しい・・・。

また今回「移動平均が移動標準偏差から 3.0 倍以上離れていたら外れ値」と定義したが、この 3.0 という数字に明確な根拠はない。ただ「ある時点でのデータの生起確率が正規分布に従う」と仮定すると、標準正規分布表 より 3.0 は .4987 なので、「標準偏差の 3.0 倍以上」は「全体の約 0.13% 以下の外れ値」とみなすことができる。