この記事はみす54代 Advent Calendar 2019の1日目として書かれてます
初めに
永続データ構造はとても強いです
殴れると嬉しいです
永続データ構造のなにが嬉しいかというと、昔のデータにアクセス出来ます
これを応用する(時間軸をY軸に見立てて使用する)事で二次元クエリにも答えられたりします
分からないところがあれば@hotmanwwにDMでもリプでも気軽に送ってください...!
1永続配列のコードと作り方
template<typename T>
struct persistent_array{
struct node;
using np=node*;
struct node{
T data;
np ch[20]={};
};
np root=nullptr;
persistent_array(){}
np get_root(){
return root;
}
np set(int idx,T val,const np& t){
np res=new node();
if(t){
memcpy(res->ch,t->ch,sizeof(t->ch));
res->data=t->data;
}
if(idx==0){
res->data=val;
}else{
res->ch[idx%20]=set(idx/20,val,res->ch[idx%20]);
}
return res;
}
T get(int idx,np t){
if(!t)return 0;
if(idx==0){
return t->data;
}else{
return get(idx/20,t->ch[idx%20]);
}
}
};
えっと、自己流です
20分木で書いています。
20の数値はlog(2,1e6)≒20から来ています(1e6くらいのサイズで一番パフォーマンスが出る構造らしい)
そもそも配列とは
配列は一つのポインタで要素の全てにアクセス出来るのでN分木と言えます
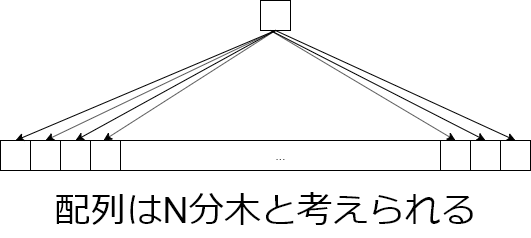
一方永続配列の構造は下のようになってます(中に入ってる数字はインデックスです)
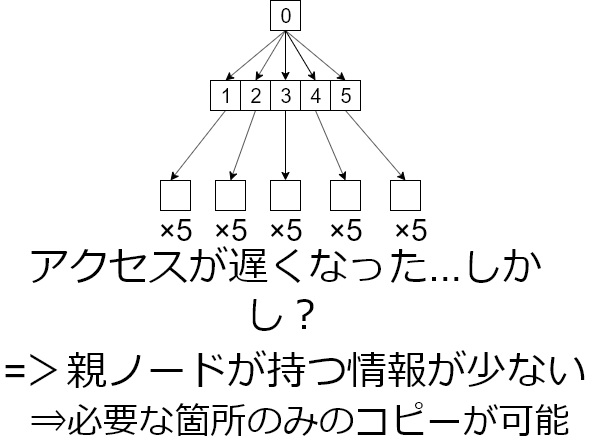
親ノードの持つ情報が少ないとどのようないいことがあるでしょうか
それは、一部のみコピーが可能という事です
例えば7番目の要素の変更を比較します
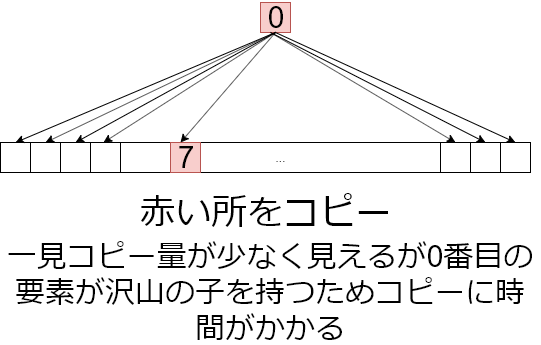
よって、永続配列は20分木くらいで作ると良さそうという事がわかりました
実装は多くは語りません、慣れようね!
node っていうstructを作ってポインタでつなげてあげるだけ!
配列のコピーはmemcpyで出来るよ!
練習問題
ABC133-F Colorful Tree
解答例
想定解では無いですが、殴って気持ちいい問題でした
頂点に情報をもたせるDFSをするのですが、子頂点の情報と親頂点の情報の差分は1なので永続配列でよしなにできます
このように差分が小さい配列が沢山作られる場合は永続配列で殴れる可能性が高いです
永続union-find木のコードと作り方
class persistent_union_find{
template<typename T>
struct persistent_array{
struct node;
using np=node*;
struct node{
T data;
np ch[20]={};
};
np root=nullptr;
persistent_array(){}
np get_root(){
return root;
}
void destructive_set(int idx,T val,np& t){
if(!t)t=new node();
if(idx==0){
t->data=val;
}else{
destructive_set(idx/20,val,t->ch[idx%20]);
}
}
np set(int idx,T val,const np& t){
np res=new node();
if(t){
memcpy(res->ch,t->ch,sizeof(t->ch));
res->data=t->data;
}
if(idx==0){
res->data=val;
}else{
res->ch[idx%20]=set(idx/20,val,res->ch[idx%20]);
}
return res;
}
T get(int idx,np t){
if(!t)return 0;
if(idx==0){
return t->data;
}else{
return get(idx/20,t->ch[idx%20]);
}
}
};
using lint=long long;
using PA=persistent_array<lint>;
PA data;
public:
using np=PA::np;
persistent_union_find(){}
np init(lint n){
np res=data.get_root();
for(lint i=0;i<n;i++)data.destructive_set(i,-1,res);
return res;
}
pair<bool,np> unite(lint x,lint y,np t){
x=root(x,t);y=root(y,t);
if(x==y)return {0,t};
if(data.get(x,t)>data.get(y,t))swap(x,y);
np res=data.set(y,x,data.set(x,data.get(x,t)+data.get(y,t),t));
return {1,res};
}
lint root(lint x,np t){
if(data.get(x,t)<0)return x;
else {
lint res=root(data.get(x,t),t);
return res;
}
}
inline bool same(lint x, lint y,np t){return root(x,t)==root(y,t);}
inline lint size(lint x,np t){return -data.get(root(x,t),t);}
};
using PUF=persistent_union_find;
using np=PUF::np;
先程の永続配列を使ってunion-find木を書いただけです
簡単ですね
特に気をつけることもありません
工夫点はdestructive_setなる関数(コピーせず更新)を作って初期化を高速化したくらいですかね
練習問題
CODE THANKS FESTIVAL 2017-H - Union Sets
解答例
やるだけです
永続セグメント木のコードと作り方
template<typename T>
class persistent_segment_tree{
struct node;
using np=node*;
using lint=long long;
struct node{
lint val;int cnt=0;
np ch[2]={nullptr,nullptr};
node(){}
node(T val):val(val){}
node(np n):val(n->val),cnt(n->cnt){ch[0]=n->ch[0];ch[1]=n->ch[1];}
};
lint sz=1,n;
int count(np t){return t?t->cnt:0;}
vector<tuple<lint,lint,T>>p;
vector<lint>x_list;
vector<np>root;
bool is_builded=0;
T e;
function<T(T,T)>f,g;
public:
persistent_segment_tree(lint n,T e,function<T(T,T)>f,function<T(T,T)>g):n(n),e(e),f(f),g(g){
while(sz<n)sz<<=1;
}
void push_back(lint x,lint y,T v){
p.emplace_back(x,y,v);
}
void build(){
is_builded=1;
sort(p.begin(),p.end());
root.resize(p.size()+1,nullptr);
x_list.resize(p.size());
for(lint i=0;i<(lint)p.size();i++){
x_list[i]=get<0>(p[i]);
root[i+1]=push_back(get<1>(p[i]),get<2>(p[i]),root[i],-sz,sz);
}
}
inline T get_fold(lint lx,lint rx,lint ly,lint ry){
return g(get_fold(ly,ry,root[lower_bound(x_list.begin(),x_list.end(),rx)-x_list.begin()],-sz,sz),get_fold(ly,ry,root[lower_bound(x_list.begin(),x_list.end(),lx)-x_list.begin()],-sz,sz));
}
inline lint get_count(lint lx,lint rx,lint ly,lint ry){
return get_count(ly,ry,root[lower_bound(x_list.begin(),x_list.end(),rx)-x_list.begin()],-sz,sz)-get_count(ly,ry,root[lower_bound(x_list.begin(),x_list.end(),lx)-x_list.begin()],-sz,sz);
}
inline lint kth_element(lint lx,lint rx,lint k){
return kth_element(root[lower_bound(x_list.begin(),x_list.end(),rx)-x_list.begin()],root[lower_bound(x_list.begin(),x_list.end(),lx)-x_list.begin()],k,-sz,sz);
}
private:
np push_back(lint pos,T val,np t,lint l,lint r){
if(l<=pos&&pos<r){
np res=t?new node(t):new node(e);
res->val=f(res->val,val);
res->cnt++;
if(r-l>1){
res->ch[0]=push_back(pos,val,res->ch[0],l,(l+r)/2);
res->ch[1]=push_back(pos,val,res->ch[1],(l+r)/2,r);
}
return res;
}else{
return t;
}
}
lint get_count(lint a,lint b,np t,lint l,lint r){
if(!t||r<=a||b<=l)return 0;
if(a<=l&&r<=b){return t->cnt;}
return f(get_count(a,b,t->ch[0],l,(l+r)/2),get_count(a,b,t->ch[1],(l+r)/2,r));
}
T get_fold(lint a,lint b,np t,lint l,lint r){
if(!t||r<=a||b<=l)return e;
if(a<=l&&r<=b){return t->val;}
return f(get_fold(a,b,t->ch[0],l,(l+r)/2),get_fold(a,b,t->ch[1],(l+r)/2,r));
}
lint kth_element(np s,np t,lint k,lint l,lint r){
if(r-l==1)return l;
if(!s)s=new node(e);
if(!t)t=new node(e);
lint cnt=count(s->ch[0])-count(t->ch[0]);
if(cnt>k)return kth_element(s->ch[0],t->ch[0],k,l,(l+r)/2);
else return kth_element(s->ch[1],t->ch[1],k-cnt,(l+r)/2,r);
}
};
上の永続セグメント木は用途を限定しています
永続セグメント木はとても沢山の事に応用出来るのでそのうちの一つである、(オフラインの)二次元クエリの処理に特化した内容です
限定的にオンラインにすることも可能です
コンストラクタでe,f,gを呼んでいますがこれはアーベル群(知らない人は調べてね!)です
push_backで頂点(x,y)に値vを置く
get_foldで[lx,rx)×[ly,ry)の領域内の点の値をコンストラクタで指定したアーベル群でfoldした値を返します
get_countで[lx,rx)×[ly,ry)の領域内の点の数を返します
kth_elementで[lx,rx)でy座標小さい方からk番目のy座標を返します
「これなんで永続セグメント木で出来るの?」って思う方多いと思います
実は、永続〇〇は二次元〇〇の代用として使える事があります
使える状況は配列v[i]と配列v[i+1]がある程度似ている事です
具体的にはxが〇〇未満である点のセグメント木、みたいなものを"追加された物の存在するx座標"ごとに作っています。
差分だけ更新すればいいのでとても永続向きですね!
これによってget_foldはxがrx未満である点のセグメント木における、[ly,ry)のfoldからxがlx未満である点のセグメント木における[ly,ry)のfoldを引けばOKという算段です
同様の理屈でget_count、kth_elementも実装出来ます(kth_elementは二分探索をします)
具体的な実装方法ですが、、
動的セグメント木と永続配列を書いたことがあれば簡単にわかると思います
セグ木の二分木をポインタで表す様にして、コピーするようにしてえいです
練習問題
Library Checker - Rectangle Sum
解答例
yosupo judgeを知っていますか?
僕は知っています
積極的に活用して行きましょう!
yukicoder-No.924 紲星
解答例
kth_elementの活用例です!
素晴らしい!
最後に
いかがでしたでしょうか
少しでも、永続〇〇制作のお役に立てたなら幸いです
初めてのアドカレなので悩みましたが、いい記事になったと自画自賛しております
MISの皆、競プロerの皆、そして全人類、一緒に永続データ構造作ろうぜ!