はじめに
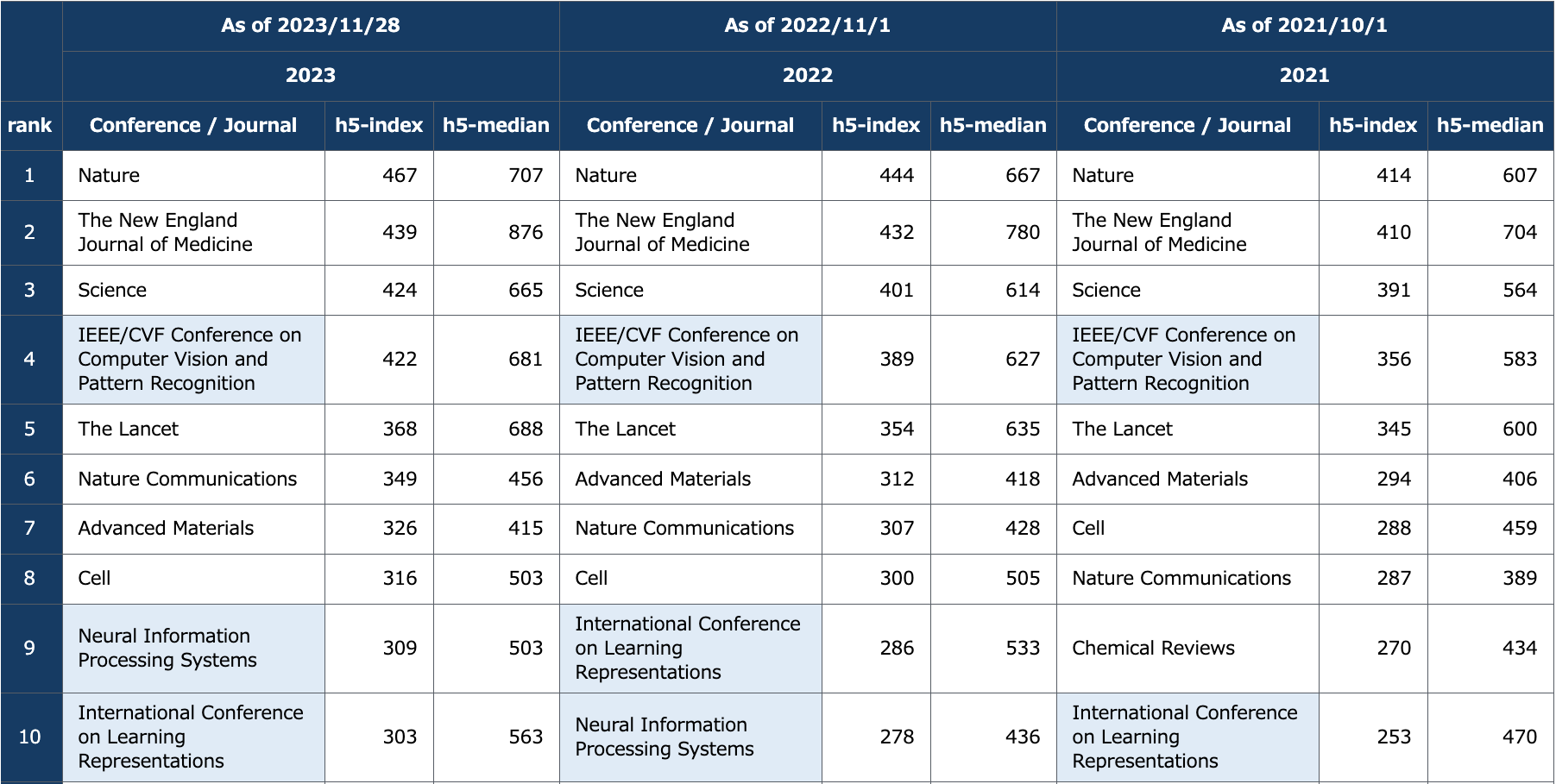
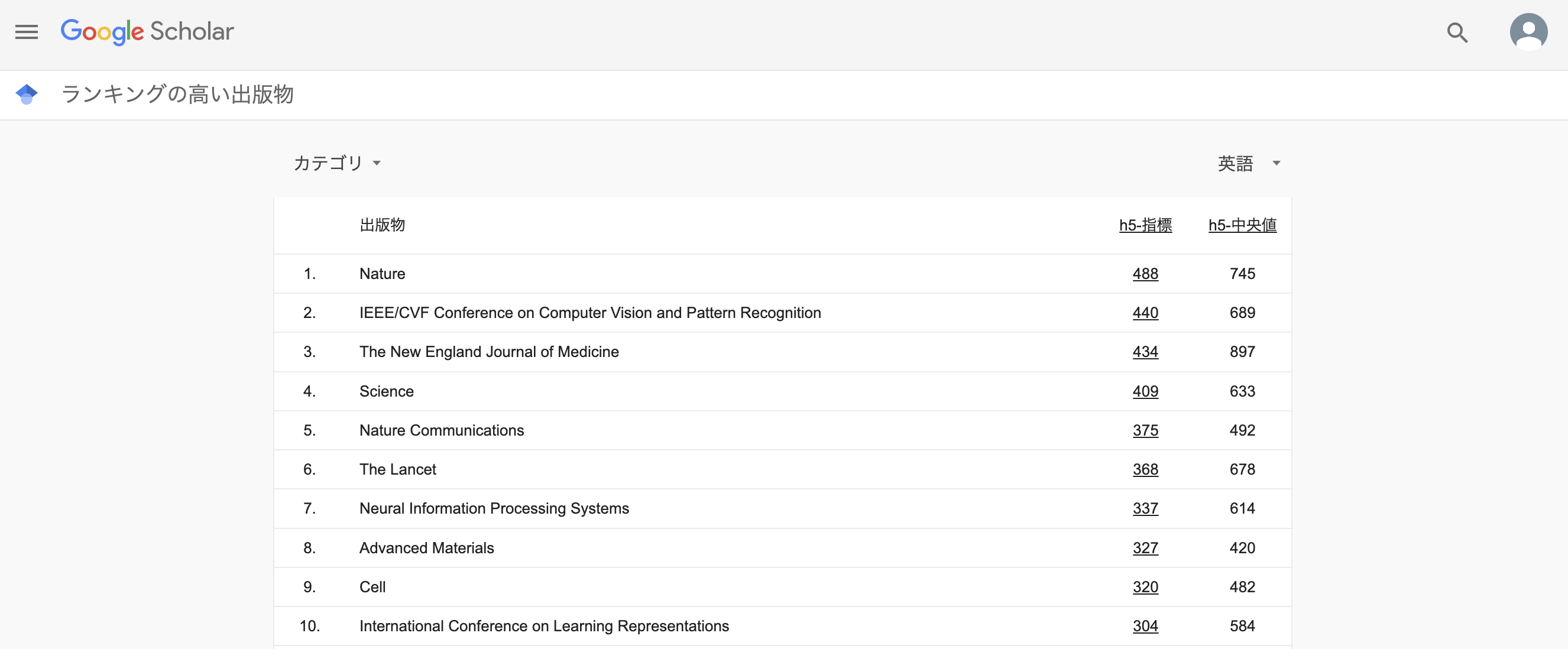
2023年まではh5-indexが4位だと言われていたCVPRがいつの間に2位に躍進しているようです(!?)
そんなCVPR2024の論文を眺めていたら、fine-tuningに関する興味深い手法、 AdaRand [Yamaguchi et al., CVPR, 2024] を見つけたので、読んで理解したところをつらつら書きていきます。
要点
- fine-tuningにおいて、特徴空間上の混合ガウス分布を用いた新たな正則化手法を提案
- sourceの情報が必要無く、重い計算やメモリ消費を回避
- 多数の既存手法と比較実験して優位性を示し、特徴空間の様子や相互情報量の観点からも解析
論文の背景と目的
- 大規模なResNetやViT、CLIPの出現により、事前学習された深層学習モデルをtarget datasetにfine-tuningすることが一般的
- target datasetが小さくとも、source domainの知識を有効活用してtarget domainに対して優れた汎化性能を発揮することもあれば、一方でtarget datasetにoverfittingしてしまうこともある
→ そのため適切な正則化手法を用いることが重要
いくつかの正則化手法はsource datasetやlabelなどの情報を必要とするが、sourceとtargetでタスクの種類が異なる場合(自己教師あり→分類)やsource datasetが公開されていない場合(CLIP)では利用できない
→ sourceの情報をせずに、かつ軽い計算コストで適用可能な正則化手法が必要
問題設定
- $K$クラス分類
- 予測器$f_\theta:\mathcal{X}\to\mathcal{Y}$
ここで、$f_\theta$は特徴抽出器$g_\phi:\mathcal{X}\to\mathbb{R}^d$と出力直前の線形層$W\in{R}^{d\times K}$に分かれるとし、$f_\theta=W^Tg_\phi$、訓練可能なパラメータは$\theta=[\phi , \ W]$
事前学習によりパラメータの初期値$\theta_s=[\phi_s , \ W_s]$が得られており、そこからtarget dataset $\mathcal{D}= \lbrace (x^i,y^i)\in \mathcal{X}\times \mathcal{Y} \rbrace_{i=1}^N$を用いて訓練
既存の正則化手法
target datasetにoverfittingさせないためには、事前学習時の知識を上手く保持することが重要だと考えられる
source domainの情報を利用しない正則化手法
-
Feature Norm Penalty (FNP) [Hariharan and Girshick, ICCV, 2017]
- $g_\phi(x)$のL1/L2ノルムで正則化
-
$L^2-SP$ [Li et al., ICML, 2018]
- パラメータについてStarting PointからのL2ノルム$||\theta - \theta_s||^2_2$で正則化
-
DELTA [Li et al., ICLR, 2019]
- $f_\theta$の中間層における出力が、$\theta = \theta_s$のときとあまり変わらないようにL2正則化
-
Batch Spectral Shrinkage (BSS) [Chen et al., NeurIPS, 2019]
- ミニバッチ内の特徴ベクトルを並べた行列の固有値に対する正則化
-
RandReg [Zhong and Maki, CVPR, 2020]
- 後述
-
Contrast-regularized tuning (Core-tuning) [Zhang et al,. NeurIPS, 2021]
- 対照学習に基づき、特徴ベクトルに対してfocal contrastive lossを適用
-
DR-Tune [Zhou et al., ICCV, 2023]
- $W$が元の$f_{\theta_s}$の特徴ベクトルの分布を利用しても分類できるように正則化項を付け加える
source domainの情報を利用した正則化手法
-
Co-tuning [You et al., NeurIPS, 2020]
- 元のsource特化のヘッド$W_s$の情報を活用する
- sourceとtargetのラベルと関係を鑑みて、source datasetをソフトラベルによるpseudo source datasetにマッピングし、target datasetと同時に学習
-
Unbalanced Optimal Transport (UOT) [Liu et al., NeurIPS, 2022]
- 最適輸送に基づくsourceとtargetのマッピングにより、target datasetに関連する部分的なsource datasetを同時に学習
-
Borrowing Treasures From the Wealthy [Ge and Yu, CVPR, 2017]
- targetに関連するsource datasetを用いる
RandReg
- 特徴ベクトルと、あるランダムなベクトルの差の最小化を目指す
- ある分布$p(z)$を用意し、$||g_\theta(x) - z||_2^2$で正則化
- $z=0$の場合にはFNPと一致
- 勾配における更新式を展開すれば、FNPの正則化の項と、摂動により局所解に陥りにくくする項と見做せる
RandRegの問題点
- $p(z)$の設定を上手く行う必要がある
- $g_\phi (x)$が実際にどれくらいのノルムになるかはデータセットやモデルごとに異なる
→ $\phi_s$におけるtarget datasetに対する特徴ベクトルの平均$\bar{\mu}_s$分散$\bar{\sigma}_s^2$で初期化したガウス分布を用いる
- $g_\phi (x)$が実際にどれくらいのノルムになるかはデータセットやモデルごとに異なる
- それでも上手く動かずFNPに劣る場合がある
- $g_\phi (x)$のノルムが特に小さくなる場合
- RandRegでは後述に実験のように、$g_\phi (x)$のノルムが制限され、特徴ベクトルの多様性が失われてしまう
- $||g_\phi (x)||_2^2$の減少
- cross entropy誤差を用いる場合、$g_\phi (x)$のノルムが小さいと$W$に関する勾配のノルムも小さくなり、上手くtarget datasetを学習できない恐れがある
- 特徴ベクトルに関するdifferential entropy $H(g_\phi (x))$の減少
- $X \subset \mathbb{R}^d$上の確率密度が$f(x)$であるときのdifferential entropy:$H(X) = - \int f(x) \log f(x) dx$
- これを手元のdatasetから推定するdifferential entropy estimatorを考える
- $x_i$まわりの$\epsilon$-ball $p(\epsilon)=\int_{||x - x_i|| < \epsilon} p(x) dx$が定数になる近似できるとき、differential entropy estimatorは$H(X)= const + \frac{d}{n(n-1)}\sum_{i \neq j}||x_i - x_j||$ で表される [Faivishevsky and Goldberger, NeurILS, 2008]
- entropyが減少すると、相互情報量が減少する
- $I(g_φ(x); y) = H(g_φ(x)) − H(g_φ(x)|y)$
- 相互情報量は、全体では多様(第1項)ながら各ラベルに関しては密集しているとき、つまり各ラベルごとのクラスタが離れていると大きくなる
- $||g_\phi (x)||_2^2$の減少
論文の提案手法:AdaRand
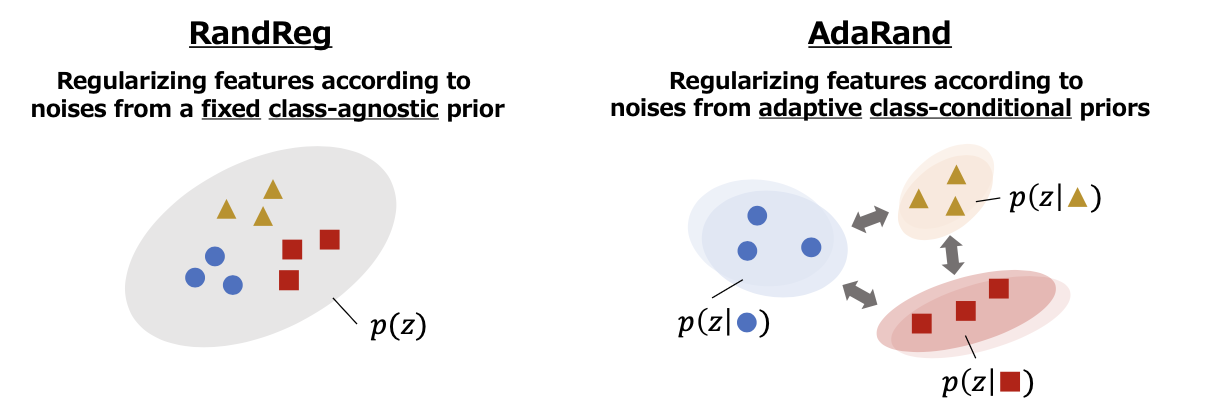
RandRegでは1つの固定の$p(z)$を使っていたところに混合ガウス分布を用いる。
$p(x) = \sum_{k=1}^K p(z|y_k)p(y_k), \ \ p(z|y_k)=\mathcal{N}(μ_k,σ_k^2I)$
パラメータ$μ_k,σ_k^2$は$g_{\phi_s}(x)$で初期化されたのち、$μ_k$は以下の目的関数を最小化するように更新されていく。
- 現在のバッチにおける各クラスの平均$\bar{μ}_k$を移動平均により計算する
$\hat{μ}_k = \frac{1}{B_k} \sum _{i=1}^{B_k}g_φ(x_i), \ \ \bar{μ}_k ← αμ ̄ _k + (1 − α)μ _k$ - 距離$D(u,v)$(たとえばコサイン距離$1 - u^Tv / ||u||_2||v||_2$)を用いて目的関数を計算する
$\mathcal{L} _{ada} = \frac{1}{K}\sum _{k=1}^K D(μ_k, \bar{μ}_k) - \frac{1}{K(K-1)}\sum _{k} \sum _{k \neq l} D(μ_k,μ_l)$ - 勾配法により$μ_k$を更新
目的関数の第1項は分布の平均を現在のデータに対する特徴ベクトルの平均に近づけるように、第2項は分布間を離すようにしている。
アルゴリズム全体としては、
-
事前学習モデルでtarget datasetに対して推論を行い$μ_k,σ_k^2$を初期化
-
各ミニバッチに対して
a. ランダムベクトルの生成- $z_i \sim p(z|y_i)$
b. モデルのパラメータ$\theta$の更新
- 目的関数: $CE(y_i, f_\theta(x_i)) + \lambda||g_\phi(x_i)-z_i||_2^2$
- 勾配法で更新
c. $p(z)$のパラメータ$\bar{\mu}$の更新
- 目的関数:$\frac{1}{K}\sum_{k=1}^K D(\mu_k, \bar{\mu} _k ) - \frac{1}{K(K-1)} \sum_k \sum _{k\neq l} D(\mu_k,\mu_l)$
- 勾配法で更新
実験結果
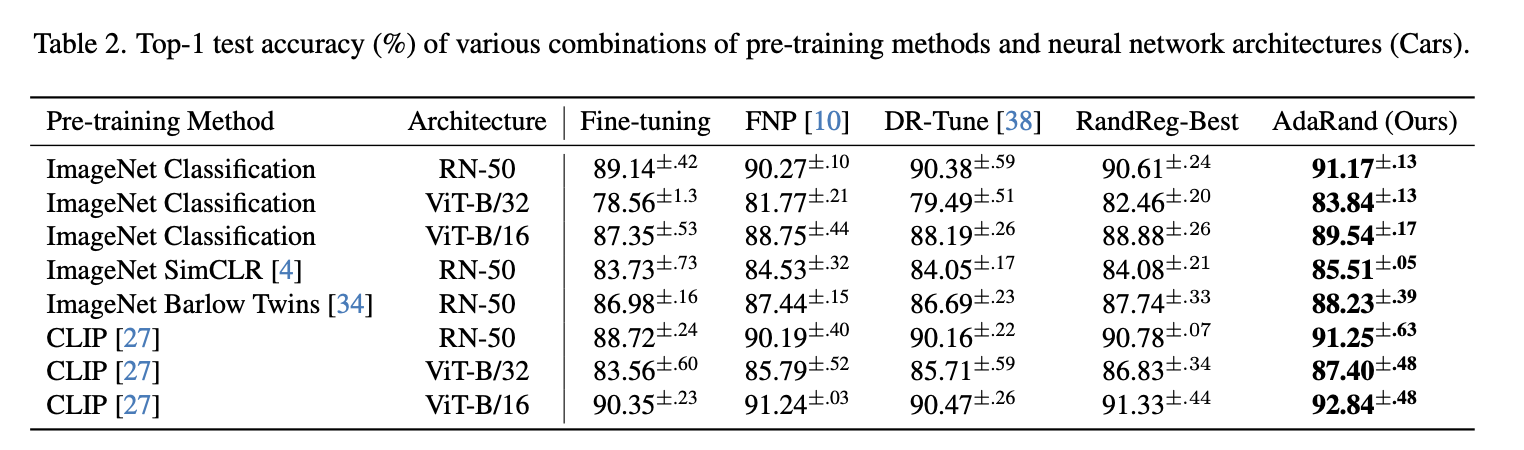
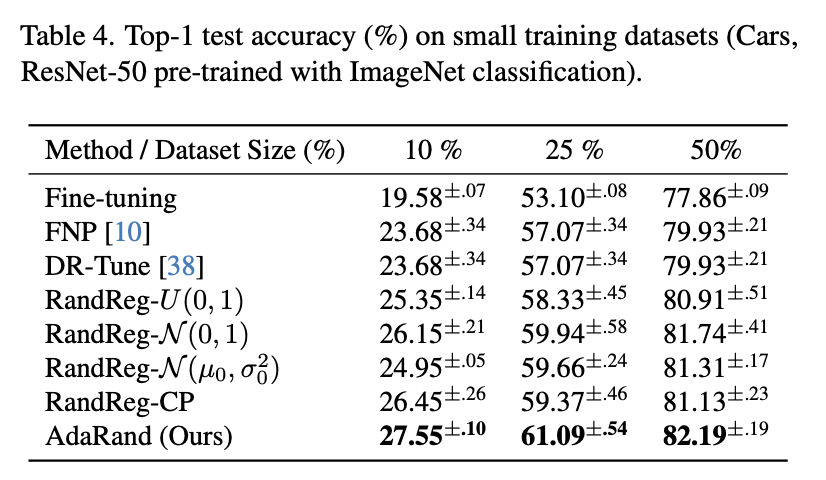
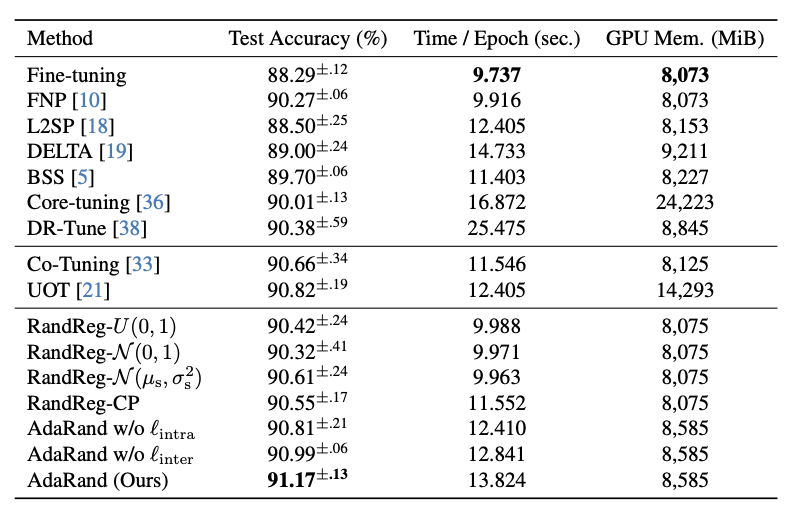
- どの事前学習モデルに対してもAdaRandが他の(source datasetを用いる手法も含めた)手法を抑えて最も精度が良い
- 少ないデータセットに対してもoverfittingしにくい
- 他手法と比較しても、計算時間をかけすぎずメモリを使い過ぎず、ある程度の計算コストに留めている
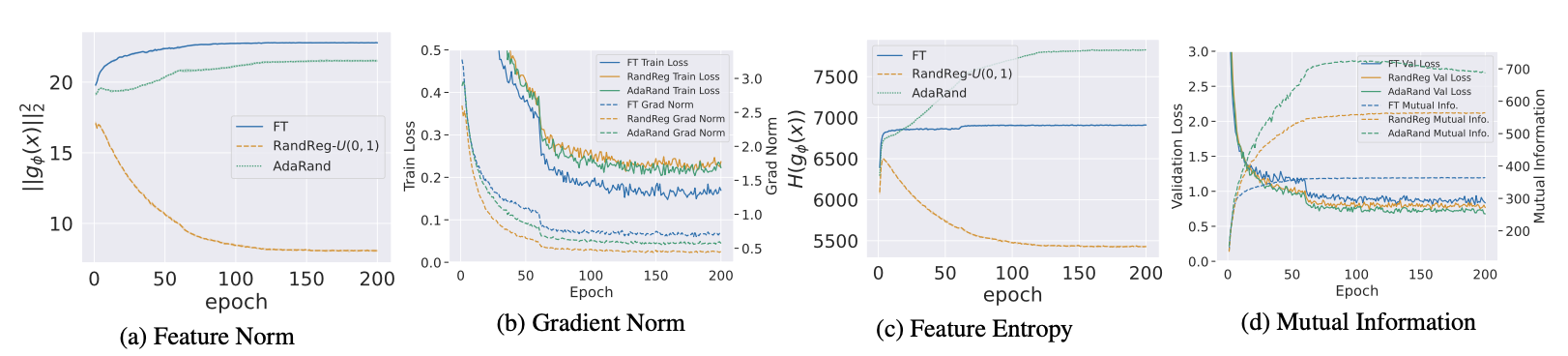
RandRegとAdaRandの比較
- 特徴ベクトルや勾配のノルムが小さくなりすぎていない
- entropyや相互情報量を最大化できている
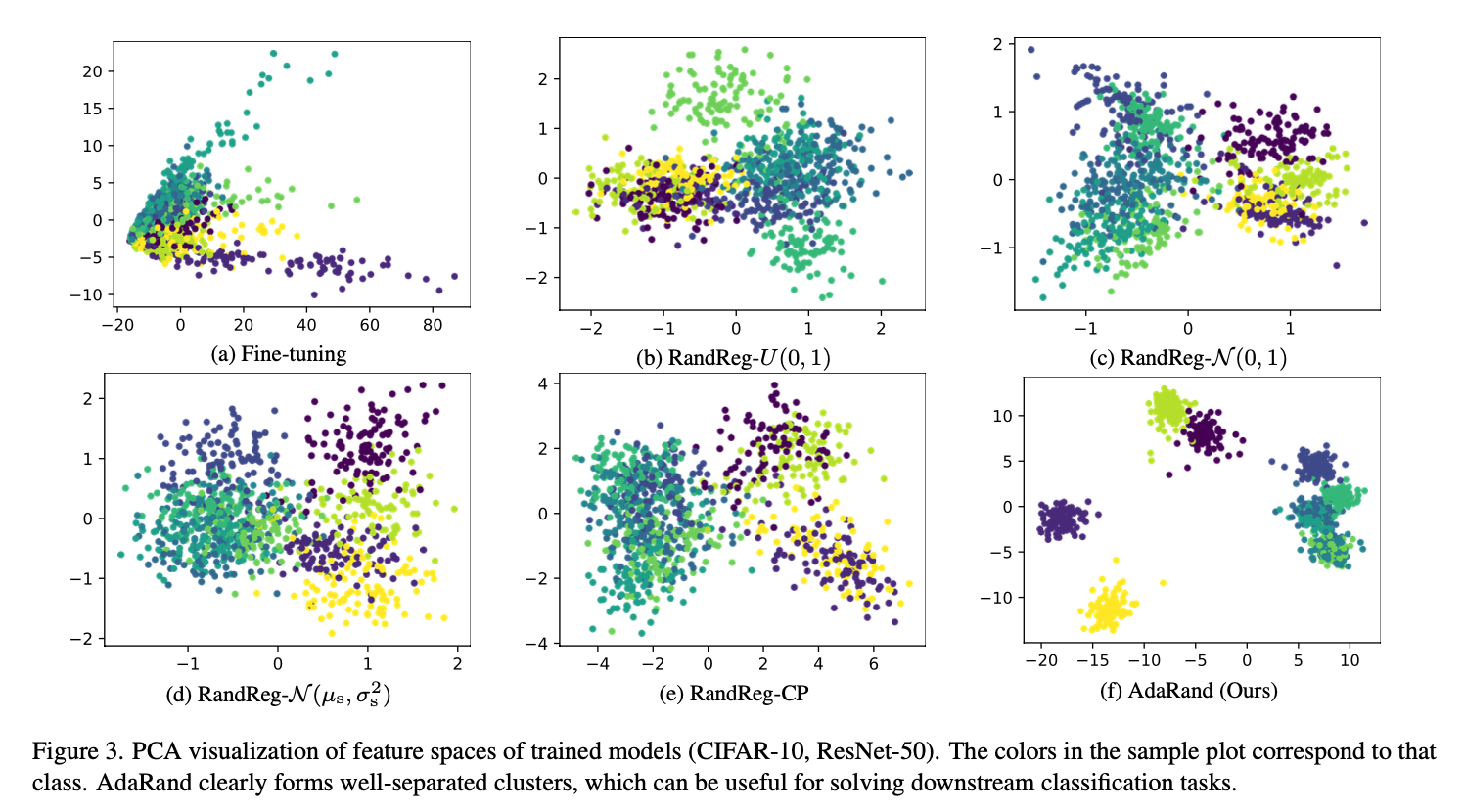
- 特徴ベクトルをPCAした結果の分布は、AdaRandではクラスごとのまとまった混合ガウス分布となっていて分類タスクで有効な特徴ベクトルの分布になっている
おわりに
読んでいて非常に面白い手法比較と有意義な分析だと思いました。
生成モデルでのfine-tuningへの拡張はfeature workとされているようですね。
何かありましたらコメントあるいはSNSアカウントにメッセージをいただければと思います。
実装
- 著者による公式実装
- Igniteを用いないミニマムな実装に書き下したver.(非公式)
- 別環境で動かしていたコードを適宜コピペしてきたので動く保証は無いです......
参考文献
Yamaguchi, S. Y., Kanai, S., Adachi, K., & Chijiwa, D. (2024). Adaptive Random Feature Regularization on Fine-tuning Deep Neural Networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (pp. 23481-23490)
Xuhong Li, Yves Grandvalet, and Franck Davoine. Explicit inductive bias for transfer learning with convolutional net- works. In International Conference on Machine Learning, 2018.
XingjianLi,HaoyiXiong,HanchaoWang,YuxuanRao,Lip- ing Liu, Zeyu Chen, and Jun Huan. Delta: Deep learning transfer using feature map with attention for convolutional networks. In International Conference on Learning Repre- sentations, 2019.
Xinyang Chen, Sinan Wang, Bo Fu, Mingsheng Long, and Jianmin Wang. Catastrophic forgetting meets negative trans- fer: Batch spectral shrinkage for safe transfer learning. In Advances in Neural Information Processing Systems, 2019.
Yang Zhong and Atsuto Maki. Regularizing cnn transfer learning with randomised regression. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 13637–13646, 2020.
YifanZhang,BryanHooi,DapengHu,JianLiang,andJiashi Feng. Unleashing the power of contrastive self-supervised visual models via contrast-regularized fine-tuning. Advances in Neural Information Processing Systems, 2021.
Nan Zhou, Jiaxin Chen, and Di Huang. Dr-tune: Improv- ing fine-tuning of pretrained visual models by distribution regularization with semantic calibration. In Proceedings of the IEEE/CVF International Conference on Computer Vision, 2023.
KaichaoYou,ZhiKou,MingshengLong,andJianminWang. Co-tuning for transfer learning. Advances in Neural Informa- tion Processing Systems, 2020.
Ziquan Liu, Yi Xu, Yuanhong Xu, Qi Qian, Hao Li, Xi- angyang Ji, Antoni B. Chan, and Rong Jin. Improved fine- tuning by better leveraging pre-training data. In Advances in Neural Information Processing Systems, 2022.
Weifeng Ge and Yizhou Yu. Borrowing treasures from the wealthy: Deep transfer learning through selective joint fine- tuning. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 1086–1095, 2017.
Lev Faivishevsky and Jacob Goldberger. Ica based on a smooth estimation of the differential entropy. In Advances in neural information processing systems, 2008.