LoginSignup
1
1

More than 3 years have passed since last update.

@hotaru_77(Kei Takamoto)

量子符号化の手法を実装してみます

Last updated at Posted at 2021-04-10

はじめに

量子コンピュータにて，古典のデータを用いた学習を行うとすると，量子系によってはどのようにその古典データを表現するのかを考えなければならない．
ここでは，その量子コンピュータへデータを読み込む方法である計算基底符号化と振幅符号化について説明を行い，qiskitによる実装を与えます．
わかりにくい箇所等あるかもしれませんがよろしくお願いします．

計算基底符号化

計算基底符号化は$n$量子ビットシステムの計算基底状態と従来の$n$ビットの配列を紐づける方法である．ある意味では，これはもっとも単純な計算方法であると言える．

例としてベクトル$\mathcal{x}=(0.1, -0.6, 1.0)$を符号化することを考える．正負を最初のビットに符号化して，残りで精度$\tau =4$の2値の分数表現で符号化すると，

\begin{align}
0.1 \to 0 \ 0001 \\
-0.6 \to 1 \ 1001 \\
1.0 \to 0 \ 1111 
\end{align}

したがって，このベクトルは量子状態$|00001 11001 01111>$と表すことができます．

計算基底符号化の理論

それぞれのデータ$\mathcal{x}^m$がビット列$\mathcal{x}^m = (b_1^m, \cdots, b_N^m)$であるような2値ので０たセット$\mathcal{D}$が与えられているとします．このデータセット$\mathcal{D}$は計算基底状態$|\mathcal{x}^m>$の重ね合わせ

|\mathcal{D}> = \frac{1}{\sqrt{M}}\sum_{m=1}^M |\mathcal{x}^m>

を用意することで表すことができます．
例として$\mathcal{x}^1=(01,01), \mathcal{x}^2=(11,01)$を計算基底状態による重ね合わせで表すと

|\mathcal{D}=\frac{1}{\sqrt{2}}|0101>+\frac{1}{\sqrt{2}}|1110>

となります．
ここからはこのデータの重ね合わせを用意する方法について説明していきたいと思います．簡単のため，2値入力に含まれる全てのビットがそれぞれ1つの特徴量を表す場合(つまりは精度$\tau =1$)を考えます．

  • step1

まず，三つのレジスタをもつ量子系が必要となります．

|l_1,\cdots, l_N;a_1, a_2; s_1, \cdots, s_N>
  • step2

左から読み込みレジスタ(loading)，補助レジスタ(ancilla)，記憶レジスタ(storage)とします．
次に補助レジスタの二番目の量子ビットにアダマールゲートを作用させます．

\frac{1}{\sqrt{2}}|0, \cdots, 0;00;0, \cdots, 0>+\frac{1}{\sqrt{2}}|0, \cdots, 0;01;0, \cdots, 0>

左の項を記憶ブランチ，右の項を処理ブランチと呼ぶことにします．
これで量子状態の準備は完了です．

次に実際にデータを符号化していくことを考えてみましょう．既に$m$個の訓練データが符号化されていて，新しく$m+1$個目のデータを符号化するとします．
既に$m$個の訓練データが符号化されている状態は次のように表すことができます．

|\psi^{(m)}>=\frac{1}{\sqrt{M}}\sum_{k=1}^{M}|0,\cdots,0;00;x_1^k,\cdots, x_N^k>
+\sqrt{\frac{M-m}{M}}|0, \cdots, 0;01;0, \cdots, 0>

記憶ブランチは既に$m$個の入力を記憶レジスタの中に持っており，処理ブランチの記憶レジスタは基底状態にあります．

$m+1$個目のデータを符号化するには，まず$m+1$個目のビット列$x^{m+1}=(x_1^{m+1},\cdots,x_N^{m+1})$を読み込みレジスタに書き込みます．これは入力ビット列が$1$の時に$X$ゲートを作用させることで実現できます．次に処理ブランチ内で読み込みレジスタから記憶レジスタへ入力ビット列をコピーします．これはトフォリゲートを使用して実現することができます．ここまでの手順によって量子状態は次のようになっています．

\frac{1}{\sqrt{M}}\sum_{k=1}^{M}|x_1^{m+1},\cdots,x_N^{m+1};00;x_1^k,\cdots, x_N^k>
+\sqrt{\frac{M-m}{M}}|x_1^{m+1},\cdots,x_N^{m+1};01;x_1^{m+1},\cdots,x_N^{m+1}>

その後補助レジスタ内でa2→a1でCNOTゲートを作用させます．
次に，1量子ビットユニタリゲート

U_{a_2}(\mu)=\frac{1}{\mu}
\left(
    \begin{array}{rr}
      \sqrt{\mu-1} & 1 \\
      -1 & \sqrt{\mu-1}
    \end{array}
  \right)

をa1に制御された形でa2に作用させます．ここで$\mu = M+1-(m+1)$です．
この演算を行うことで処理ブランチを二つの下位ブランチに分割します．

\frac{1}{\sqrt{M}}\sum_{k=1}^{M}|x_1^{m+1},\cdots,x_N^{m+1};00;x_1^k,\cdots, x_N^k>
+\frac{1}{\sqrt{M}}|x_1^{m+1},\cdots,x_N^{m+1};10;x_1^{m+1},\cdots,x_N^{m+1}>
+\sqrt{\frac{M-(m+1)}{M}}|x_1^{m+1},\cdots,x_N^{m+1};11;x_1^{m+1},\cdots,x_N^{m+1}>

$|a_1 a_2>$を記憶ブランチに付け加えるには，この下位ブランチの$a_1$を$0$に戻す必要がある．最後に処理ブランチの記憶レジスタと全てのブランチの読み込みレジスタを初期化すれば終了である．

計算基底符号化の実装

理論的には量子計算を少し学んだ者なら簡単に理解できると思うが，実際に実装を行ってみると難所がいくつかある．それら全てを解決しながら実装を行ってみました．ここでも量子回路を記述する手法としてQiskitを使用します．

とりあえず使用するライブラリーをimport

computational_basis.py
from qiskit import QuantumRegister, QuantumCircuit, ClassicalRegister
from qiskit import Aer, execute
import numpy as np

初期設定及び，使用するデータセット

backend = Aer.get_backend('qasm_simulator')

N = 2
M = 3
data_set = [[1, 1], [1, 0], [0, 1]]

続いて各レジスタを設定して量子回路を作成します．

loading_reg = QuantumRegister(N, name='loading')
ancilla_reg = QuantumRegister(2, name='ancilla')
storage_reg = QuantumRegister(N, name='storage')
reserve_reg = QuantumRegister(N, name='reserve')
mct_ancilla = QuantumRegister(N, name='mct_ancilla')
classical_reg = ClassicalRegister(N)
circuit = QuantumCircuit(loading_reg, ancilla_reg, storage_reg, reserve_reg, mct_ancilla, classical_reg)

ここでreserve_regは初期化の際に使用するレジスタ，mct_ancillaはマルチコントロールゲートを使用する際の補助レジスタとしています．
次にstep2の実装ですが，通常はアダマールを作用させますがここでは別で作成したユニタリー演算子$U$

U= \frac{1}{\sqrt{M}}
\left(
\begin{array}{rr}
1 & -\sqrt{M-1} \\
\sqrt{M-1} & 1
\end{array}
\right)

をアダマールゲートの代わりに作用させます．
理論通りにアダマールを作用させてしまうと$M=2$の時のみに対応する形になってしまい，最初に符号化されたデータが量子状態の半分を占めてしまうことになってしまうからです．
その関数がこちら

def initial_hadamard(M):
    # 回路を準備
    qc = QuantumCircuit(1, name='hadamard')
    # ユニタリー演算子を定義
    unit = np.array([[1, -np.sqrt(M-1)], [np.sqrt(M-1), 1]])
    unit *= 1 / np.sqrt(M)
    # ゲートとして回路に作用させる
    qc.unitary(unit, [0])
    # ゲートに変換して返す
    return qc.to_gate()

gate = initial_hadamard(M)
circuit.append(gate, [N+1]) # hadamard gateの代わり

またここでも新たに作成した関数を差し込みます．
理論のままだと既に$|0,\cdots,0>$というデータが格納されているということになってしまっているのでそこを改良します．

def first_data(circuit, loading_reg, ancilla_reg, storage_reg, my_data, N):
    # 読み込みレジスタにデータを入力
    loading(circuit, loading_reg, my_data)
    # 処理ブランチの記憶レジスタにコピー 
    all_ccnot(circuit, loading_reg, ancilla_reg, storage_reg, N, X=True)
    # 読み込みレジスタを初期化
    loading(circuit, loading_reg, my_data)
    return circuit

first_data(circuit, loading_reg, ancilla_reg, storage_reg, data_set[0], N)

それぞれの関数については後ほど説明します．
この作業を行うことによって$|0,\cdots,0>$が含まれることを防ぎます．(もちろんデータとしてある場合はやらなくて良いと思います）

ここからは実際にデータを符号化していくプログラムになります．先に使用する関数を説明します．

def loading(circuit, loading_reg, my_data):
    # データを読み込みレジスタに書き込む
    for d in range(len(my_data)):
        if my_data[d] == 1:
            circuit.x(loading_reg[d])
    return circuit


def all_ccnot(circuit, loading_reg, ancilla_reg, storage_reg, N, X=False):
    # 処理ブランチの記憶レジスタにコピーする
    # Xはfirst dataの時のみに使用する
    if X is True:
        circuit.x(ancilla_reg[1])
    for n in range(N):
        circuit.ccx(loading_reg[n], ancilla_reg[1], storage_reg[n])
    if X is True:
        circuit.x(ancilla_reg[1])
    return circuit


def U_a2(mu):
    # ユニタリー演算子を作成
    qc = QuantumCircuit(1, name='Ua2')
    unit = np.array([[np.sqrt(mu - 1), 1], [-1, np.sqrt(mu - 1)]])
    unit *= 1 / np.sqrt(mu)
    qc.unitary(unit, [0])
    # .control(1)で制御することが可能になる
    return qc.to_gate().control(1)


def match(circuit, loading_reg, reserve_reg, ancilla_reg, mct_ancilla, N):
    # 同じかどうかを判定する回路を作成する
    # 基本的には読み込みレジスタと処理レジスタが同じかどうかをCNOTを用いて比較
    # reserveレジスタで判定する
    for n in range(N):
        circuit.cx(loading_reg[n], reserve_reg[n])
        circuit.cx(storage_reg[n], reserve_reg[n])
    circuit.x(reserve_reg[:])
    circuit.x(ancilla_reg[1])

    control_qubits = [[N+1] + [q for q in range(N*2+2, N*3+2)]
    circuit.mct(control_qubits, ancilla_reg[0], mct_ancilla)
    # 一緒で10ならばa1をflipさせて元に戻すけど（最初に全体をflipさせているのでa2をflip)
    circuit.x(ancilla_reg[1])
    return circuit


def initialize(circuit, loading_reg, ancilla_reg, storage_reg, N, my_data):
    # 初期化する
    circuit.cx(ancilla_reg[1], ancilla_reg[0])
    all_ccnot(circuit, loading_reg, ancilla_reg, storage_reg, N)
    loading(circuit, loading_reg, my_data)
    return circuit

では実際に符号化していきます．

# data_set[0]は既に符号化済
for m in range(1, M):

    my_data = data_set[m]
    loading(circuit, loading_reg, my_data)

    all_ccnot(circuit, loading_reg, ancilla_reg, storage_reg, N)

    circuit.cx(ancilla_reg[1], ancilla_reg[0])

    mu = M + 1 - (m + 1)
    Ua2 = U_a2(mu)
    circuit.append(Ua2, [N, N+1])

    match(circuit, loading_reg, reserve_reg, ancilla_reg, mct_ancilla, N)

    initialize(circuit, loading_reg, ancilla_reg, storage_reg, N, my_data)

    circuit.reset(reserve_reg)
    circuit.reset(mct_ancilla)

では符号化できているかどうか測定して確認をしてみましょう．

circuit.measure(storage_reg, classical_reg)

result = execute(circuit, backend, shots=8192).result()
counts = result.get_counts()
print(counts)

'''
{'01': 2734, '10': 2796, '11': 2662}
'''

良い感じにできてますね．

振幅符号化

振幅符号化は実数ベクトルなどの古典的な情報を量子振幅と関連付ける．

振幅符号化の理論

今ここに規格化された古典的なベクトル$\mathcal{x}\in \mathbb{C}^{2^n}$があるとします．

\mathcal{x}=[x_1,\cdots, x_{2^n}]^T

これを振幅符号化した量子状態は

|\psi_x>=\sum_{j=1}^{2^n}x_j|j>

と表されます．
と言った様に雑に言えば簡単ですね（これを実装するのが大変なんだが...)

振幅符号化の実装

振幅符号化のキーとなるのはmulti-controlled rotation gateです．量子ビット$q_s$に対する回転を前の量子ビット$q_1, \cdots, q_{s-1}$のとりうる全ての状態によって制御します，全ての状態というのは，例えば$s=3$に対する制御を考えると前にある量子ビット$q_1, q_2$のとりうる全ての状態というのは$00, 01, 10, 11$の四つとなります．

では，$q_1, \cdots, q_{s-1}$の状態が$|0,\cdots,0>$である時，$q_s$に作用させるゲートはどうなるのでしょうか．このゲートは次の式で表されます．

c_{q_1=0}\cdots c_{q_{s-1}=0}R_{q_s}(\mathcal{v}^1, \beta_1)|q_1\cdots q_{s-1}>|q_s>

となります．個でを全ての状態について行いますので，他のゲートは次の様に表されます．

\begin{align}
c_{q_1=0}\cdots c_{q_{s-1}=1}R_{q_s}(&\mathcal{v}^2, \beta_2)|q_1\cdots q_{s-1}>|q_s> \\
&\vdots \\ 
c_{q_1=1}\cdots c_{q_{s-1}=1}R_{q_s}(&\mathcal{v}^{2^{s-1}}, \beta_{2^{s-1}})|q_1\cdots q_{s-1}>|q_s>
\end{align}

振幅符号化では$R_y$ゲートを使用していきます．また，各$\beta$については次の式で求めることができます．

\beta_j^s = 2arcsin(\frac{\sqrt{\sum_{l=1}^{2^{s-1}}|\alpha_{(2j-1)2^{s-1}+l}|^2}}{\sqrt{\sum_{l=1}^{2^{s}}|\alpha_{(j-1)2^{s}+l}|^2}}

この＄\beta＄の添字$s$は量子ビットのインデックス，$j$は$s-1$までの量子ビットがとりうる全ての状態のインデックスとなっています．

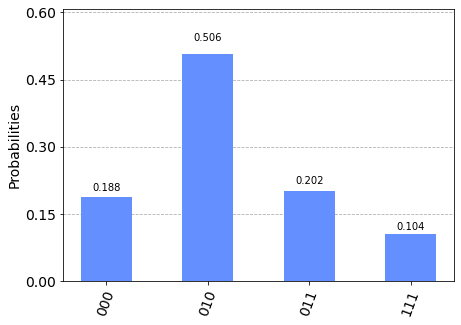
ここで例をあげます．状態$|\psi>=\sqrt{0.2}|000>+\sqrt{0.5}|010>+\sqrt{0.2}|110>+\sqrt{0.1}|111>$を作りたいと考えます．
この時の振幅はすなわち$\alpha_1=\sqrt{0.2},\alpha_3=\sqrt{0.5},\alpha_7=\sqrt{0.2},\alpha_8=\sqrt{0.1}$です．(一般的に振幅を表すときは$\alpha_0$から始めると思いますが，整合性を保つためにここではこの様な表記の仕方をしたいと思います．)

この時の量子回路には七つの複数制御$y$回転ゲート

\begin{align}
c_{q1=0}c_{q2=0} R_{y,q_3}(\beta_1^1), \beta_1^1 &= 0 \\
c_{q1=0}c_{q2=1} R_{y,q_3}(\beta_2^1), \beta_2^1 &= 0 \\
c_{q1=1}c_{q2=0} R_{y,q_3}(\beta_3^1), \beta_3^1 &= 0 \\
c_{q1=1}c_{q2=1} R_{y,q_3}(\beta_4^1), \beta_4^1 &= 1.231... \\
c_{q1=0} R_{y,q_2}(\beta_1^2), \beta_1^2 &= 2.014... \\
c_{q1=1} R_{y,q_2}(\beta_2^2), \beta_2^2 &= 3.142... \\
R_{y,q_1}(\beta_1^3), \beta_1^3 &= 1.159... 
\end{align}

この時の$\beta_1^1,\beta_1^2$を例として計算式を挙げてみます．

\begin{align}
\beta_1^1 &= 2arcsin(\frac{\sqrt{|\alpha_2|^2}}{\sqrt{|\alpha_1|^2 +|\alpha_2|^2}}) \\
\beta_1^2 &= 2arcsin(\frac{\sqrt{|\alpha_3|^2+|\alpha_4|^2}}{\sqrt{|\alpha_1|^2 +|\alpha_2|^2+|\alpha_3|^2+|\alpha_4|^2}})
\end{align}

この様に計算されています．

実際にpythonとQiskitを用いて振幅符号化の実装を行っていきましょう．まずはimportからです．

amplitude.py
from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister
from qiskit import Aer, execute
import numpy as np

# 自作ライブラリ
from Functions.Binary import dec2bin_for_counts

初期値を設定します．ここでは先程紹介した例を実装していきます．

if __name__ == '__main__':
    backend = Aer.get_backend('qasm_simulator')

    amplitude_data = [0.2, 0, 0.5, 0, 0, 0, 0.2, 0.1]

    nQ = 3

回路の準備です．ancilla_regを複数制御回転ゲート用に用意しておきます．

    # 回路を準備
    encode_reg = QuantumRegister(nQ, name='encode')
    ancilla_reg = QuantumRegister(nQ, name='ancilla')
    output_reg = ClassicalRegister(nQ, name='measure')
    circuit = QuantumCircuit(encode_reg, ancilla_reg, output_reg)

ここで二つの関数を定義します．

# beta_j^sを求める関数
def beta_js(amplitude_data, j, s):
    denominator = 0 # 分母
    numerator = 0 # 分子
    for l in range(0, 2**s):
        denominator += abs(amplitude_data[(j-1)*(2**s)+l])
    for l in range(0, 2**(s-1)):
        numerator += abs(amplitude_data[(2*j-1)*(2**(s-1))+l])
    if denominator == 0:
        return 0.
    else:
        return 2*np.arcsin(np.sqrt(numerator)/np.sqrt(denominator))

# 二進数表記で1ならばx gateをapplyする関数
def apply_x_gate(circuit, bin2, s_):
    for i in range(len(bin2)):
        if bin2[i] == '0':
            circuit.x(s_-i-1)
    return circuit

# 複数制御回転ゲートを実際に行う関数
def mcry_for_encode(circuit, encode_reg, ancilla_reg, bin2, beta):
    apply_x_gate(circuit, bin2)
    # multi-controlled ry gate
    circuit.mcry(beta, encode_reg[:len(bin2)], encode_reg[len(bin2)], ancilla_reg)
    apply_x_gate(circuit, bin2)
    return circuit

実際にencodeしていきます．

    # 全てのsに対してloop
    for s in range(1, nQ+1):
        s_ = nQ-s
        # 全てのjに対してloop
        for j in range(1, 2**s_+1):
            beta = beta_js(amplitude_data, j, s)
            bin2 = dec2bin_for_counts(j-1, s_)
            if bin2 is True:
                circuit.ry(beta, 0)
            else:
                if beta == 0.:
                    pass
                else:
                    mcry_for_encode(circuit, encode_reg, ancilla_reg, bin2, beta)

この回路を逆演算に変換します．

   inverse_circuit = circuit.inverse()

実際に測定を行いencodeできているか確認しましょう．

    # 測定する
    inverse_circuit.measure(encode_reg, output_reg)

    result = execute(inverse_circuit, backend=backend, shots=1000).result()
    counts = result.get_counts()
    print(counts)
    '''
    {'000': 188, '010': 506, '011': 202, '111': 104}
    '''

amplitude_encode.png

良い感じの結果になりましたね．

最後に

今回は計算基底符号化と振幅符号化の実装を行いました．他にもいくつか符号化の方法があると思いますが，それはまた別の機会に実装を行いたいと思います．
また，他にも符号化について細かい理論等あるとは思いますが，私個人の興味がこの符号化を用いたものの先にあるのでここでは割愛させていただきたいと思います．

1
1
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
1
1