はじめに
AtCoder で緑の先を目指そうと、競プロ典型 90 問 - AtCoder に取り組んでいます。その中で 029 - Long Bricks (★5) が面白く、複数の方法で解こうとしてみました。
- 029 - Long Bricks(★5)
- 問題と解説 (Twitter) E869120 さん公式
- 解説 - 競プロ典型 90 問 rsk0315さんユーザー解説
複数の方法で解こうとして、多くは計算量に負けて TLE (Time limit exceeded) しました。それも含めてアルゴリズムを見比べてみます。
想定読者
- (Rust で) AtCoder に参加している
- 用語とコード例は Rust です。図の部分は C++ など他の言語で解いている方も大丈夫なつもりです。
- D, E 問題で TLE と戦っている
- フェニック木、平方分割、セグメント木の名前を知っている
- AtCoder Library を使いたい
- rust-lang-ja/ac-library-rs: ac-library-rs is a rust port of AtCoder Library (ACL). は C++ 版のように AtCoder サーバー上には置いていません。使うにはひと手間かかります
今回の対象外
- 平方分割、セグメント木に乗せるデータの条件 (モノイドとは何か など)
- 空間計算量
- データ構造の選択で、時間計算量 (速度) と空間計算量 (消費メモリー) を組みで考えることも多いです
- 競技プログラミングでは時間内に動けば良いので、あまり気にしません
問題
問題は AcCoder 側、または Twitter 側をどうぞ。
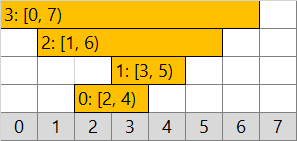
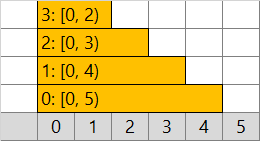
例題1 の入力イメージです。
100 4 # 幅 W = 100 (座標1~100), 入力数 N = 4
27 100 # 0: 27~100 の区間にブロックを置く
8 39 # 1: 8~ 39 の区間にブロックを置く
83 97 # 2: 83~ 97 の区間にブロックを置く
24 75 # 3: 24~ 75 の区間にブロックを置く
本記事中では配列の開始を 0 とし、半開区間で考えます。例えば「27~100 の区間」という入力を「[26, 100) = 26 以上 100 未満の区間」と読み替えます。 1
解答
| 方法 | データ構造 | 区間絞り込み | 区間最大値取得 | 区間更新 | 結果 |
|---|---|---|---|---|---|
| 1. シンプルな方法 | Vec | $O(N)$ | $O(NW)$ | $O(NW)$ | TLE * 6 |
| 2. 座標圧縮 | Vec | $O(N)$ | $O(N^2)$ | $O(N^2)$ | TLE * 4 |
| 3. 不要な座標を消す | Vec | $O(NlogN)$ | $O(N)$ | $O(N^2)$ | TLE * 1 |
| 4. 単方向リストを併用する | Vec | $O(N^2)$ | $O(N)$ | $O(N)$ | TLE * 3 |
| 5. 木構造セットを併用する | BTreeSet | $O(NlogN)$ | $O(NlogN)$ | $O(NlogN)$ | AC |
| 6. 木構造マップを使用する | BTreeMap | $O(NlogN)$ | $O(NlogN)$ | $O(NlogN)$ | AC |
| 7. フェニック木でセットを作る | Vec | $O(NlogN)$ | $O(NlogN)$ | $O(NlogN)$ | AC |
| 8. 平方分割する | Vec | $O(N)$ | $O(N\sqrt{W})$ | $O(N\sqrt{W})$ | AC |
| 9. 遅延評価セグメント木を使用する | Vec | $O(NlogW)$ | $O(NlogW)$ | $O(NlogW)$ | AC |
「500,000 個のデータを扱うこの問題は、$O(N^2)$ がどこかに現れるとタイムアウト」で終わります。
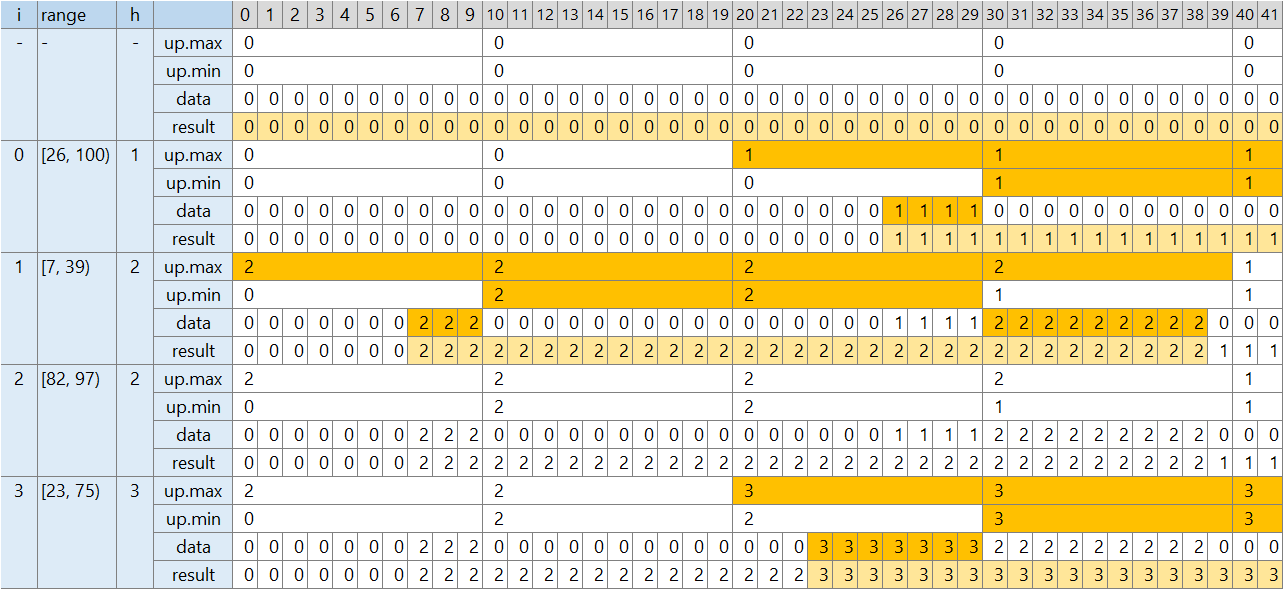
1. シンプルな方法 (TLE * 6)
要素数 W の配列 v に対して、次のように処理します。
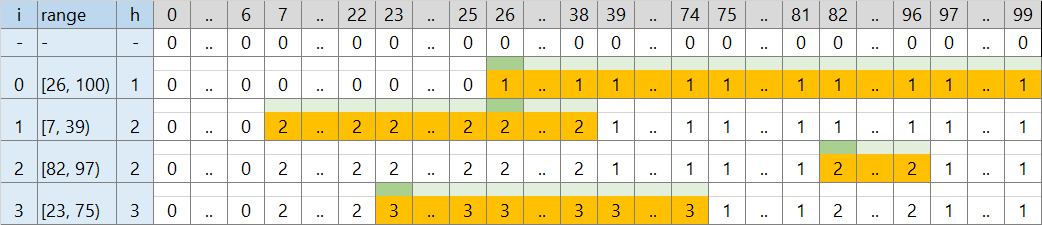
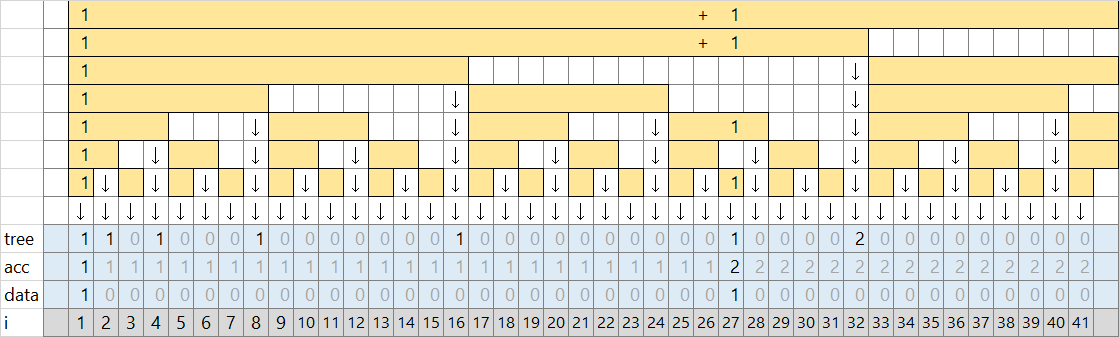
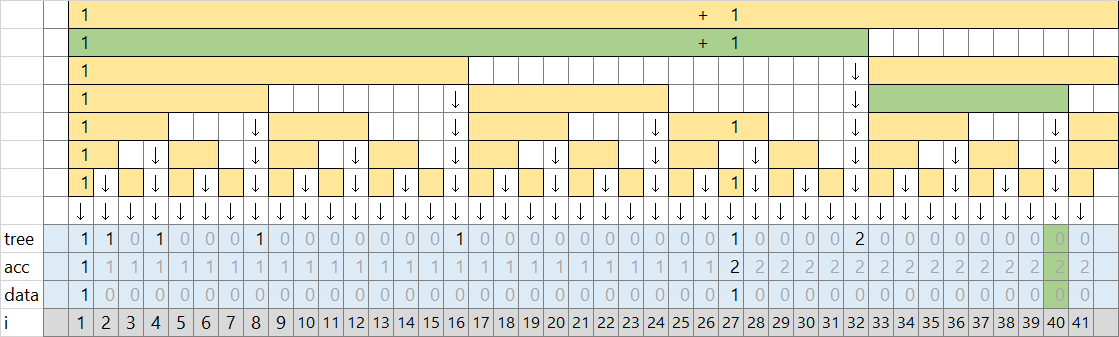
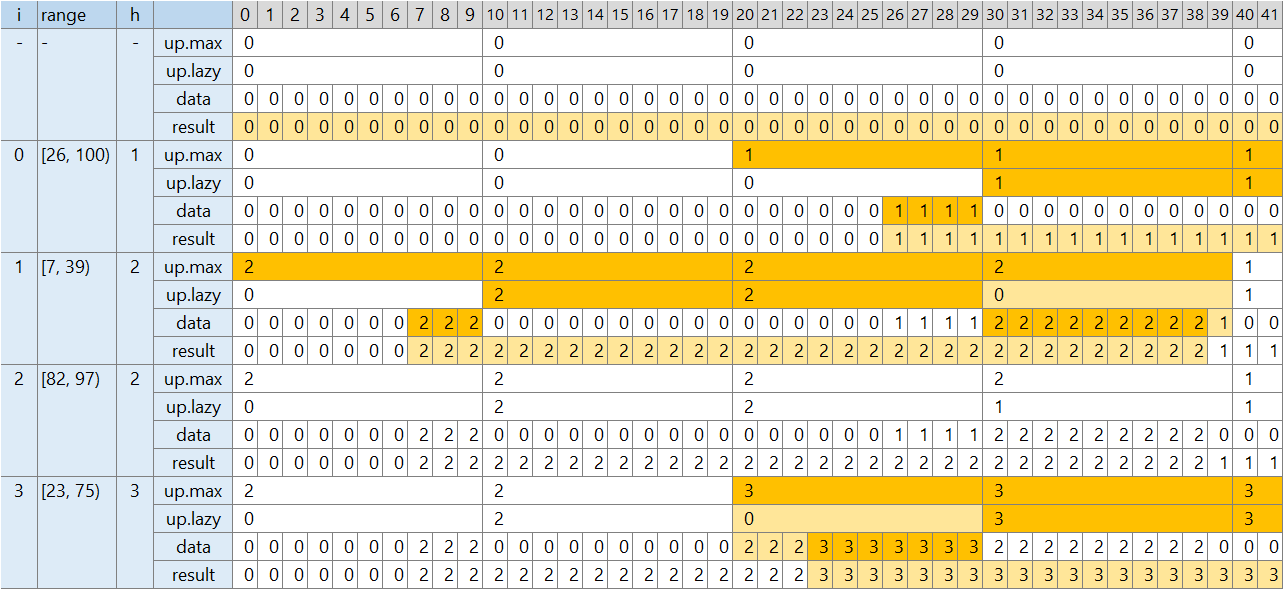
- [26, 100) の区間を処理する
- v の [26, 100) の区間内 (74個) で最大の値を探す → 0 (緑)
- v の [26, 100) の区間内 (74個) の値を 0 + 1 = 1 に書き換える (オレンジ)
- [7, 39) の区間を処理する
- v の [7, 39) の区間内 (32個) で最大の値を探す → 1 (緑)
- v の [7, 39) の区間内 (32個) の値を 1 + 1 = 2 に書き換える (オレンジ)
区間内の最大の値を探すところ、区間内の値をすべて書き換えるところとも、区間の長さだけ繰り返します。幅 100 なら大丈夫でも、[0, 500000) のような広い区間が複数回現れるとタイムアウトしそうです。
コード
use proconio::{input, marker::Usize1};
fn main() {
input! {
w: usize,
lr: [(Usize1, Usize1)],
}
let mut v = vec![0usize; w];
for &(l, r) in &lr {
let height = v[l..=r].iter().max().unwrap() + 1;
for h in v[l..=r].iter_mut() {
*h = height;
}
println!("{}", height);
}
}
2. 座標圧縮 (TLE * 4)
幅すべてに対して配列のインデックスを割り当てる代わりに、高さが変わりうるところだけ割り当てることにします。
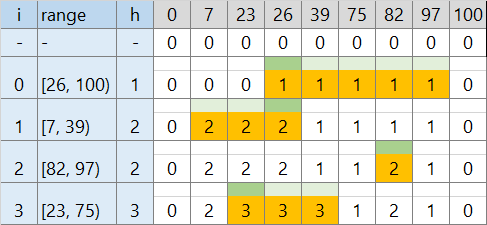
- 座標圧縮した配列を作成する
- [26, 100), [7, 39), [82, 97), [23, 75) と、初期サイズの [0, 100) をあわせると、値が変わるのは 9 箇所だけ
- [26, 100) の区間を処理する
- v の [26, 100) の区間内 (5個) で最大の値を探す → 0 (緑)
- v の [26, 100) の区間内 (5個) の値を 0 + 1 = 1 に書き換える (オレンジ)
- [7, 39) の区間を処理する
- v の [7, 39) の区間内 (3個) で最大の値を探す → 1 (緑)
- v の [7, 39) の区間内 (3個) の値を 1 + 1 = 2 に書き換える (オレンジ)
シンプルな 1. よりは調べる数・更新数とも減ります。入力数が少ない場合は効果がありそうです。
ただし幅に対して入力数が多いと、圧縮効果がないこともあります。たとえば次のようなデータでは圧縮効果がありません。効果は「入力数 N が少ない」という追加制約 2. に頼ったものとなります。
コード
use proconio::{input, marker::Usize1};
fn init_cv(w: usize, lr: &[(usize, usize)]) -> (Vec<usize>, usize) {
let mut v = Vec::with_capacity(lr.len() * 2 + 2);
v.push(0);
v.push(w);
for &(l, r) in lr {
v.push(l);
v.push(r + 1);
}
v.sort();
v.dedup();
let mut cv = vec![0; w + 1];
for (i, &x) in v.iter().enumerate() {
cv[x] = i;
}
(cv, v.len())
}
fn main() {
input! {
w: usize,
lr: [(Usize1, Usize1)],
}
let (cv, len) = init_cv(w, &lr);
let mut v = vec![0usize; len];
for &(l, r) in &lr {
let l0 = cv[l];
let r0 = cv[r + 1];
let height = v[l0..r0].iter().fold(0, |acc, &x| acc.max(x)) + 1;
for x in v[l0..r0].iter_mut() {
*x = height;
}
println!("{}", height);
}
}
3. 不要な座標を消す (TLE * 1)
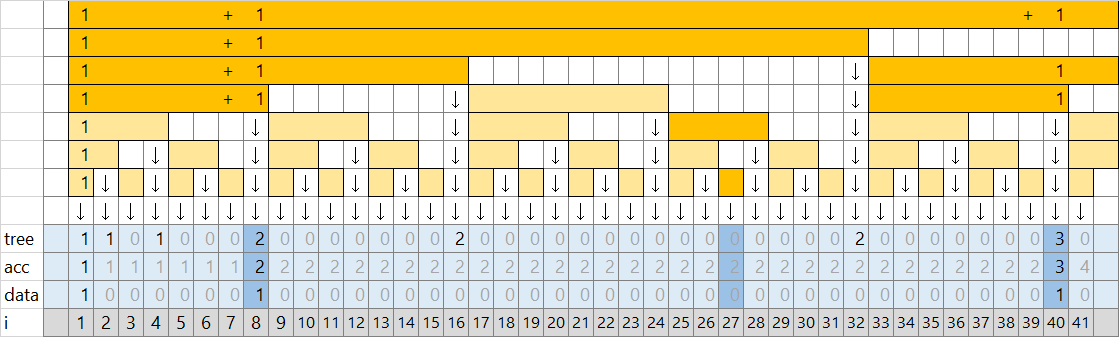
座標圧縮でそれぞれ更新する数は減りました。それでも同じ値を連続して書き込むところは変わりませんでした。
上がほかのブロックで覆われた後は、もうその場所で高さが変化することはないはずです。下の図で×の部分を更新する必要はありません。
そこで、値が変わる座標だけ管理し、不要になった座標はその都度管理対象外にします。
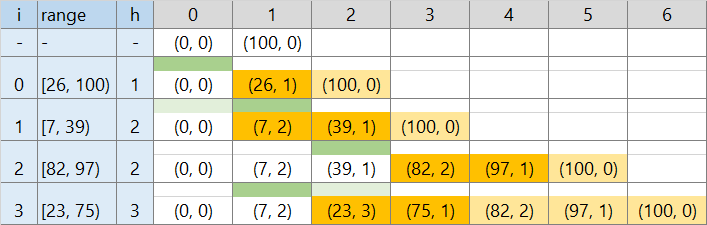
- [0, 100) が高さ 0 と、配列 v を初期設定する
- → v には [0, 100] の 2 つの座標だけが入っている
- [26, 100) の区間を処理する
- v から 26 以下の位置を二分探索で探す (lower_bound 2)
- v から 100 以下の位置を二分探索で探す
- この半開区間の最大値を調べる → 0 (緑)
- [26, 100) に含まれる位置情報を削除し、その場所に [26, 100) 両端対応する位置情報を挿入する (オレンジ)
- → v には [0, 26, 100] の 3 つの座標だけが入っている
- [7, 39) の区間を処理する
- v から 7 以下の位置を二分探索で探す
- v から 39 以下の位置を二分探索で探す
- この半開区間の最大値を調べる → 1 (緑)
- [7, 39) に含まれる位置情報を削除し、その場所に [7, 39) 両端対応する位置情報を挿
- → v には [0, 7, 29, 26, 100] の 4 つの座標だけが入っている
位置情報の挿入・削除の回数はせいぜい操作数 N * 2 です。これで終了。
……と言いたいところですが、配列内の挿入・削除はとても遅いです。C++, Rust など多くの言語では配列をメモリー内の連続領域で表現しています。挿入・削除しようとするとその区間だけメモリーのコピーが発生します。
最悪ケースでこのようなデータを扱うと、右にコピーする数が操作のたびに増えていきます。 $O(N^2)$ 回のコピーとなります。
ダメもとで実装してみたところ、やっぱり 1 つ TLE しました。
コード
use proconio::{input, marker::Usize1};
use superslice::Ext;
fn main() {
input! {
w: usize,
lr: [(Usize1, Usize1)],
}
let mut v = Vec::with_capacity(w + 1);
v.push((0usize, 0usize));
v.push((w, 0));
for &(l, r) in &lr {
let l0 = v.lower_bound_by(|x| x.0.cmp(&l));
let r0 = v.lower_bound_by(|x| x.0.cmp(&(r + 1)));
let l1 = if v[l0].0 == l { l0 } else { l0 - 1 };
let r1 = if r0 < v.len() && v[r0].0 == r + 1 {
r0
} else {
r0 - 1
};
let height = v[l1..r0].iter().fold(0, |acc, x| acc.max(x.1)) + 1;
let h_r1 = v[r1].1;
let mut ins = Vec::with_capacity(2);
if l0 == 0 || v[l0 - 1].1 != height {
ins.push((l, height));
}
if h_r1 != height {
ins.push((r + 1, h_r1));
}
v.splice(l0..=r1, ins);
println!("{}", height);
}
}
もしかするとこの方針でも工夫すれば AC できるかもしれません。今回は諦めました。 3
4. 単方向リストを併用する (TLE * 3)
配列内の挿入・削除が遅いなら、代わりの方法を考えます。隣の有効な座標を辿れれば良いです。 C++ で言う std::list 構造が使えます。
- [0, 100) が高さ 0 と、配列 v を初期設定する
- → v には "0 の次は 100" という情報が入っている。ほかはアクセスしない予定なので何でもよい
- [26, 100) の区間を処理する
- v の先頭 26 以下の位置を順に辿る
- そこからさらに順に辿り、100 以下の区間での最大高さを調べる → 座標 0 の値 0 (緑)
- "0 の次は 26", "26 の高さは 0 + 1 = 1", "26 の次は 100" という情報を追加する (オレンジ)
- → v を先頭から辿ると [0, 26, 100] の 3 つの座標だけ通る
- [7, 39) の区間を処理する
- v の先頭 7 以下の位置を順に辿る
- そこからさらに順に辿り、39 以下の区間での最大高さを調べる → 座標 26 の値 1 (緑)
- "0 の次は 7", "7 の高さは 1 + 1 = 2", "7 の次は 39", "39 の次は 100 (26 の次と同じ)" という情報を追加する (オレンジ)
- 26 x はもう辿れないので、値を更新する必要はない
- → v を先頭から辿ると [0, 3, 39, 100] の 4 つの座標だけ通る
このようにすると配列の内側の挿入・削除は行わなくて良くなります。しかしどの位置が有効かがすぐには分かりません。先頭から毎回辿ることになります。
そうすると次のような入力に弱くなります。操作のたびに辿る数が 1 つずつ増えていきます。最悪ケースで $O(N^2)$ です。
単方向リストで書いたところ、やはり TLE しました。
コード
use proconio::input;
use proconio::marker::Usize1;
fn prev_lower_bound(vi: &[usize], i: usize) -> usize {
let mut j = 0;
while i > vi[j] {
j = vi[j];
}
j
}
fn max_height(vh: &[usize], vi: &[usize], l: usize, r: usize) -> usize {
let mut h_max = vh[l];
let mut j = vi[l];
while j <= r {
h_max = h_max.max(vh[j]);
j = vi[j];
}
h_max
}
fn main() {
input! {
w: usize,
lr: [(Usize1, Usize1)],
}
let mut vh = vec![0usize; w + 1]; // vec<height>
let mut vi = vec![0usize; w + 1]; // vec<next_index>
vi[0] = w;
for &(l, r) in &lr {
let l0 = prev_lower_bound(&vi, l + 1);
let r0 = prev_lower_bound(&vi, r + 1);
let r1 = vi[r0];
let height = max_height(&vh, &vi, l0, r0) + 1;
vi[l0] = l;
if r1 == r + 1 {
vi[l] = r1;
} else {
vi[l] = r + 1;
vi[r + 1] = r1;
vh[r + 1] = vh[r0];
}
vh[l] = height;
println!("{}", height);
}
}
5. 木構造セットを併用する (AC)
先ほどは「有効な位置の探索が遅い」ことで困りました。この問題は「有効な位置を二分探索」できるデータ構造があれば解消します。
はい、Rust BTreeSet や C++ std::set がそのまま使えます。
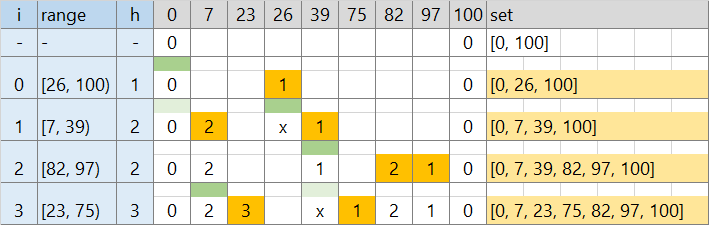
- [0, 100) が高さ 0 と配列 v を初期設定し、セット s に有効な座標として 0, 100 を登録する
- [26, 100) の区間を処理する
- s の 26 以下の最後の座標を調べる → 0
- s の 100 以下の最後の座標を調べる → 100
- この区間での最大高さを調べる → 座標 0 の値 0 (緑)
- s の有効な座標に 26 を追加し、v に "26 の高さは 0 + 1 = 1" を追加する (オレンジ)
- [7, 39) の区間を処理する
- s の 7 以下の最後の座標を調べる → 0
- s の 39 以下の最後の座標を調べる → 26
- この区間での最大高さを調べる → 座標 26 の値 1 (緑)
- s の有効な座標から 26 を削除する
- 26 x はもう辿れないので、v の値を更新する必要はない
- s の有効な座標に 7 を追加し、v に "7 の高さは 1 + 1 = 2" を追加する (オレンジ)
- s の有効な座標に 39 を追加し、v に "39 の高さは 1 (座標 26 と同じ)" を追加する (オレンジ)
これで AC です。お疲れさまでした。 4
コード
use std::collections::BTreeSet;
use std::ops::Bound::{Excluded, Unbounded};
use proconio::input;
use proconio::marker::Usize1;
fn main() {
input! {
w: usize,
lr: [(Usize1, Usize1)],
}
let mut v = vec![0usize; w + 1]; // vec<height>
let mut s = BTreeSet::new(); // available indices
s.insert(0usize);
s.insert(w);
for &(l, r) in &lr {
let hl = v[*s.range((Unbounded, Excluded(l + 1))).last().unwrap()];
let hr = v[*s.range((Unbounded, Excluded(r + 2))).last().unwrap()];
let mut height = hl + 1;
while let Some(&i) = s.range((Unbounded, Excluded(r + 1))).last() {
if i <= l {
break;
}
height = height.max(v[i] + 1);
s.remove(&i);
}
v[l] = height;
s.insert(l);
v[r + 1] = hr;
s.insert(r + 1);
println!("{}", height);
}
}
6. 木構造マップを使用する (AC)
配列とセットの組み合わせで解きました。この 2 つをひとまとめにしたデータ構造があれば良いです。はい、Rust BTreeMap や C++ std::map がそのまま使えます。
これで 1 通り増やしたことにするのはなんだかとも思いますが、別実装ということで。
コード
use std::collections::BTreeMap;
use std::ops::Bound::{Excluded, Unbounded};
use proconio::input;
use proconio::marker::Usize1;
fn main() {
input! {
w: usize,
lr: [(Usize1, Usize1)],
}
let mut m = BTreeMap::new();
m.insert(0usize, 0usize);
m.insert(w, 0);
for &(l, r) in &lr {
let (_, &hl) = m.range((Unbounded, Excluded(l + 1))).last().unwrap();
let (_, &hr) = m.range((Unbounded, Excluded(r + 2))).last().unwrap();
let mut height = hl + 1;
while let Some((&i, &h)) = m.range((Unbounded, Excluded(r + 1))).last() {
if i <= l {
break;
}
height = height.max(h + 1);
m.remove(&i);
}
m.insert(l, height);
m.insert(r + 1, hr);
println!("{}", height);
}
}
7. フェニック木でセットを作る
二分探索できるセットやマップを使える言語なら、この方針に気づけば終わりです。しかし残念ながらハッシュのセット・マップしか標準ライブラリーでは使えない言語もあります。
そんなときにはフェニック木 (Binary Indexed Tree)。フェニック木は累積和の更新を効率的に行えます。セットを「累積和の値が変わる場所に座標が存在する」とみなせばよいです。
フェニック木の値更新
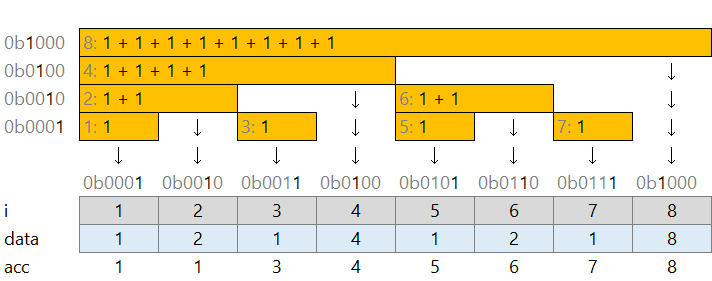
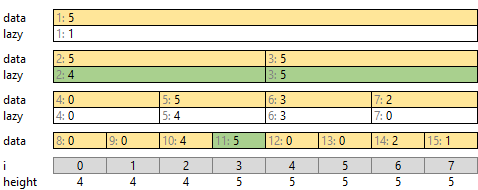
8 要素の配列に [1, 1, 1, .. 1] と、すべて 1 が入っているとします。累積和は [1, 2, 3, ... 8] となります。 これを下図のように 2 進数のビットが並ぶ感じで部分的に合計を取ったものの組を data = [1, 2, 1, 4, ...] と管理します。
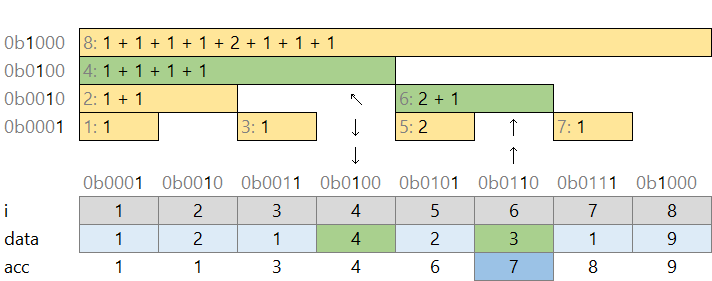
この配列の 5 番目を 1 から 2 に変更しようとします。普通の累積和配列では、5 番目以降のすべての値を書き換えました。フェニック木では上に辿った場所の値を書き換えれば良いです。
- 5 の 1 つ上: 0b0101 の一番右の有効ビットが 0b0001 。これを足して 5 + 1 = 6
- 6 の 1 つ上: 0b0110 の一番右の有効ビットが 0b0010 。これを足して 6 + 2 = 8
フェニック木の累積和計算
累積和を計算したい時は、木から欲しいかたまりの組を取ってきます。たとえば 1 番目から 6 番目までの合計は、「1 ~ 4 番目の和」「5 ~ 6 番目の和」の 2 つから計算できます。こちらは左に辿った場所の値を参照すれば良いです。
- 6 の 1 つ左: 0b0110 の一番右の有効ビットが 0b0010 。これを引いて 6 - 2 = 4
- 4 の 1 つ左: 0b0100 の一番右の有効ビットが 0b0100 。これを引いて 4 - 4 = 0 。ここで打ち止め
更新も累積和計算も $O(log N)$ とひと手間かかりますが、両方行いたいときには効率が良いです。
7-A. フェニック木で解く (AC)
例えば以下の最後の処理を考えます。この中だけフェニック木で扱いやすいように配列のインデックスを1開始とします。
- [1, 101) の区間を処理する
- セットに [1, 101] の 3つの座標が存在する
- [27, 101) の区間を処理する
- セットに [1, 27, 101] の 3つの座標が存在する
- [8, 40) の区間を処理する
[27, 101) を処理した時点で、データ構造はこのようになっています。フェニック木は "tree" のような配列を管理しています。
次に [8, 40) のそれぞれの lower_bound を調べます。図では 40 の方を調べます。40 の累積和は緑の合計で 2 です。累積和が 2 になる最初の場所を二分探索で調べます。そうすると 27 が見つかります。
8 の方も同様に行い、lower_bound 0 を得ます。今後 8 と 40 は座標を確認する対象としてセットに追加し、27 は取り除きます。
このようにすれば高速に二分探索できます。5. で使っていた BTreeSet をこちらに置き換えて 5 、AC しました。
コード
use proconio::{input, marker::Usize1};
struct FenwickTree(Vec<i64>);
struct FenwickTreeSet(FenwickTree);
impl FenwickTree {
pub fn add(&mut self, mut i: usize, x: i64) {
while i < self.0.len() {
self.0[i] += x;
i += i & i.wrapping_neg(); // i & -i
}
}
pub fn sum(&self, mut i: usize) -> i64 {
let mut sum = 0;
while i > 0 {
sum += self.0[i];
i -= i & i.wrapping_neg(); // i & -i
}
sum
}
fn lower_bound(&self, x: i64) -> usize {
if x == 0 {
return 0;
}
let data = &self.0;
let mut l = 0;
let ceil_pow2 = 32 - ((data.len() as u32) - 1).leading_zeros();
let mut len = 1 << ceil_pow2;
while len > 0 {
let i = l + len;
if i < data.len() && self.sum(i) < x {
l = i;
}
len = len >> 1;
}
l
}
pub fn new(n: usize) -> Self {
FenwickTree(vec![0; n])
}
}
impl FenwickTreeSet {
pub fn new(n: usize) -> Self {
FenwickTreeSet(FenwickTree::new(n + 1))
}
pub fn lower_bound(&mut self, i: usize) -> usize {
self.0.lower_bound(self.0.sum(i + 1))
}
pub fn contains(&mut self, i: usize) -> bool {
self.0.sum(i + 1) - self.0.sum(i) > 0
}
pub fn insert(&mut self, i: usize) {
if !self.contains(i) {
self.0.add(i + 1, 1);
}
}
pub fn remove(&mut self, i: usize) {
if self.contains(i) {
self.0.add(i + 1, -1);
}
}
}
fn main() {
input! {
w: usize,
lr: [(Usize1, Usize1)],
}
let mut v = vec![0usize; w + 1];
let mut s = FenwickTreeSet::new(w + 1);
s.insert(0);
s.insert(w);
for &(l, r) in &lr {
let hl = v[s.lower_bound(l)];
let hr = v[s.lower_bound(r + 1)];
let mut height = hl + 1;
loop {
let i = s.lower_bound(r);
if i <= l {
break;
}
height = height.max(v[i] + 1);
s.remove(i);
}
v[l] = height;
s.insert(l);
v[r + 1] = hr;
s.insert(r + 1);
println!("{}", height);
}
}
7-B. lower_bound を部分木を辿るよう変更 (AC)
前のコードは lower_bound() を累積和に対して二分探索していました。
木を上から順に部分木のどちらを辿るか調べるように 3 行書き換えると、二分処理時間が $O(N (log W)^2)$ から $O(N log W)$ に減ります。より効率的です。
前のものでも AC が取れますので、この問題については頑張らなくて良いですが、一応貼っておきます。
コード
use proconio::{input, marker::Usize1};
struct FenwickTree(Vec<i64>);
struct FenwickTreeSet(FenwickTree);
impl FenwickTree {
pub fn add(&mut self, mut i: usize, x: i64) {
while i < self.0.len() {
self.0[i] += x;
i += i & i.wrapping_neg(); // i & -i
}
}
pub fn sum(&self, mut i: usize) -> i64 {
let mut sum = 0;
while i > 0 {
sum += self.0[i];
i -= i & i.wrapping_neg(); // i & -i
}
sum
}
fn lower_bound(&self, mut x: i64) -> usize {
if x == 0 {
return 0;
}
let data = &self.0;
let mut l = 0;
let ceil_pow2 = 32 - ((data.len() as u32) - 1).leading_zeros();
let mut len = 1 << ceil_pow2;
while len > 0 {
let i = l + len;
if i < data.len() && data[i] < x {
x -= data[i];
l += len;
}
len = len >> 1;
}
l
}
pub fn new(n: usize) -> Self {
FenwickTree(vec![0; n])
}
}
impl FenwickTreeSet {
pub fn new(n: usize) -> Self {
FenwickTreeSet(FenwickTree::new(n + 1))
}
pub fn lower_bound(&mut self, i: usize) -> usize {
self.0.lower_bound(self.0.sum(i + 1))
}
pub fn contains(&mut self, i: usize) -> bool {
self.0.sum(i + 1) - self.0.sum(i) > 0
}
pub fn insert(&mut self, i: usize) {
if !self.contains(i) {
self.0.add(i + 1, 1);
}
}
pub fn remove(&mut self, i: usize) {
if self.contains(i) {
self.0.add(i + 1, -1);
}
}
}
fn main() {
input! {
w: usize,
lr: [(Usize1, Usize1)],
}
let mut v = vec![0usize; w + 1];
let mut s = FenwickTreeSet::new(w + 1);
s.insert(0);
s.insert(w);
for &(l, r) in &lr {
let hl = v[s.lower_bound(l)];
let hr = v[s.lower_bound(r + 1)];
let mut height = hl + 1;
loop {
let i = s.lower_bound(r);
if i <= l {
break;
}
height = height.max(v[i] + 1);
s.remove(i);
}
v[l] = height;
s.insert(l);
v[r + 1] = hr;
s.insert(r + 1);
println!("{}", height);
}
}
8. 平方分割する
これまで不要な座標を削っていたのは、区間の更新が遅いためでした。「平方分割」「セグメント木」のように区間を効率的に扱えるデータ構造を使うという方法もあります。まずは比較的簡単な平方分割から。
平方分割の概要
100 個の高さを扱う際に、追加で「$Sqrt{100}$個の親階層」を作ります。この親階層に「区間全体の最大高さ」情報を持つようにします。そうすると、ある区間の最大値を探すときに、上の階層を併用することで確認する場所の数が減ります。
[0, 20) なら 20 か所調べていたところが 2 か所になります。
これで値の取得は高速になりましたが、残念ながらこの構造では値の更新については遅いままです。[0, 30) の高さが更新されたときに 上の階層だけ書き換えたくなります。そうすると [3,6) などの小さな区間の最大値が欲しくなった時に正しい値が取れません。
そこで、親階層にもう 1 つの情報も登録することにします。この方法を 2 通り考えます。
8-A. 平方分割 + 遅延展開 (AC)
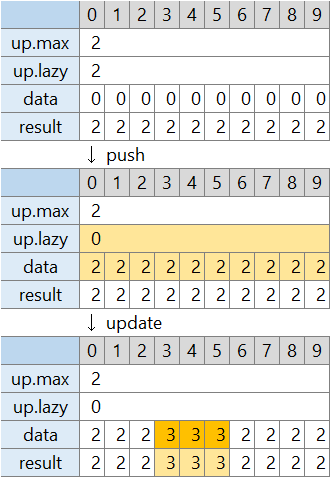
lazy の中に 0 以外の値が入っている場合に、「この区間の値は、すべて末端の data と lazy のうち大きな方」と扱うことにします。そうすると大きな区間の更新時には、両端以外は親階層にある「最大値、lazy」だけを書き換えれば良いです。
親階層の「lazy」が入っているときに、末端の一部の値を更新したくなると、そのときにはじめて lazy の値を配れば良いです。配るのには時間がかかりますが、一部だけ更新したい場所は区間の両端だけですので、心配しなくても大丈夫です。
全体の流れです。
- [0, 100) が高さ 0 と配列 data を初期設定し、10 要素の親階層 up も初期設定する
- [26, 100) の区間を処理する
- [26, 100) の最大高さを調べる → 0
- [26, 30) の最大高さ → 0
- [30, 100) の最大高さを、親階層 [3, 10) の「区間全体の最大高さ」から得る → 0
- [26, 100) の高さに 0 + 1 = 1 を入れる
- [26, 30) の最大高さに 1 を書き込む
- [20, 30) を示す親階層 [2] の 「区間全体の最大高さ」 を、現在の値 0 と 1 の大きな方に置き換える
- [30, 100) を示す親階層 [3, 10) の 「区間全体の最大高さ」 を、現在の値 0 と 1 の大きな方に置き換える
- [30, 100) を示す親階層 [3, 10) の 「区間全体の高さ lazy」 を、現在の値 0 と 1 の大きな方に置き換える
- [26, 100) の最大高さを調べる → 0
- [7, 39) の区間を処理する
- [7, 39) の最大高さを調べる → 1
- [7, 10) の最大高さを調べる
- [0, 10) の「区間全体の高さ lazy」を使って、末端の data を更新し、lazy を 0 にする
- [0, 10) の最大高さを得る → 0
- [10, 30) の最大高さを、親階層 [3, 10) の「区間全体の最大高さ」から得る → 1
- [30, 39) の最大高さを調べる
- [30, 39) の「区間全体の高さ lazy」を使って、末端の data を更新し、lazy を 0 にする
- [30, 39) の最大高さを得る → 1
- [7, 10) の最大高さを調べる
- [7, 39) の高さに 1 + 1 = 2 を入れる
- [7, 10) の最大高さに 2 を書き込む
- [7, 10) を示す親階層 [0] の 「区間全体の最大高さ」 を、現在の値 0 と 2 の大きな方に置き換える
- [10, 30) を示す親階層 [1, 3) の 「区間全体の最大高さ」 を、現在の値 0 と 2 の大きな方に置き換える
- [10, 30) を示す親階層 [1, 3) の 「区間全体の高さ lazy」 を、現在の値 0 と 2 の大きな方に置き換える
- [30, 39) の最大高さに 2 を書き込む
- [30, 39) を示す親階層 [0] の 「区間全体の最大高さ」 を、現在の値 1 と 2 の大きな方に置き換える
- [7, 39) の最大高さを調べる → 1
言葉にすると長く難しそうですが、コードとしては単純です。これで AC を取れます。
二分木を使った log に比べると、√ でしかない平方分割は遅いです。実装が非効率だと定数倍の壁に負けて TLE してしまうこともあります。ありました。
コード
use num_integer::Roots;
use proconio::input;
use proconio::marker::Usize1;
struct Btree {
data: Vec<usize>,
up_size: usize,
up_data: Vec<usize>,
up_lazy: Vec<usize>,
}
impl Btree {
pub fn new(n: usize) -> Self {
let up_size = (n - 1).sqrt() + 1;
let data = vec![0; up_size * up_size];
let up_data = vec![0; up_size];
let up_lazy = vec![0; up_size];
Btree {
data,
up_size,
up_data,
up_lazy,
}
}
fn push(&mut self, k: usize) {
let lazy = self.up_lazy[k];
if lazy == 0 {
return;
}
let n = self.up_size;
for i in (k * n)..((k + 1) * n) {
self.data[i] = self.data[i].max(lazy);
}
self.up_lazy[k] = 0;
}
pub fn update(&mut self, l: usize, r: usize, x: usize) {
let n = self.up_size;
let mut l0 = l / n;
let r0 = r / n;
if l0 == r0 {
self.up_data[l0] = self.up_data[l0].max(x);
for i in l..r {
self.data[i] = x;
}
} else {
if l % n > 0 {
self.up_data[l0] = self.up_data[l0].max(x);
for i in l..((l0 + 1) * n) {
self.data[i] = x;
}
l0 += 1;
}
if l0 < r0 {
for i in l0..r0 {
self.up_data[i] = x;
self.up_lazy[i] = x;
}
}
if r % n > 0 {
self.up_data[r0] = self.up_data[r0].max(x);
for i in (r0 * n)..r {
self.data[i] = x;
}
}
}
}
pub fn prod(&mut self, l: usize, r: usize) -> usize {
let n = self.up_size;
let mut l0 = l / n;
let r0 = r / n;
let mut x = 0;
if l0 == r0 {
self.push(l0);
x = x.max(*self.data[l..r].iter().max().unwrap());
} else {
if l % n > 0 {
self.push(l0);
x = x.max(*self.data[l..((l0 + 1) * n)].iter().max().unwrap());
l0 += 1;
}
if l0 < r0 {
x = x.max(*self.up_data[l0..r0].iter().max().unwrap());
}
if r % n > 0 {
self.push(r0);
x = x.max(*self.data[(r0 * n)..r].iter().max().unwrap());
}
}
x
}
}
fn main() {
input! {
w: usize,
lr: [(Usize1, Usize1)],
}
let mut t = Btree::new(w);
for &(l, r) in &lr {
let height = t.prod(l, r + 1) + 1;
t.update(l, r + 1, height);
println!("{}", height);
}
}
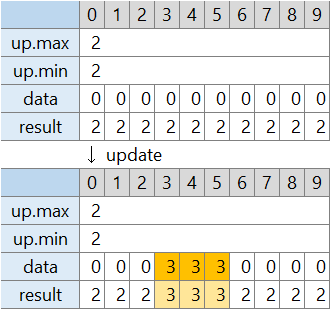
8-B. 平方分割 + 「高さがこれ以上」補助情報 (AC)
遅延展開だと値のコピーに時間がかかりました。この問題では別に配らなくてもそのままで良いです。
区間内の最大値を調べるときに、親階層の一部にかかるものは「lazy 高さがこれ以上」も含めて最大値を調べれば良い、というだけです。
この方法で少し流れを書き換えて実行しました。
流れ (8-1. とだいたい同じため折り畳み)
- [0, 100) が高さ 0 と配列 data を初期設定し、10 要素の親階層 up も初期設定する
- [26, 100) の区間を処理する
- [26, 100) の最大高さを調べる → 0
- [26, 30) の最大高さ → 0
- [30, 100) の最大高さを、親階層 [3, 10) の「区間全体の最大高さ」から得る → 0
- [26, 100) の高さに 0 + 1 = 1 を入れる
- [26, 30) の最大高さに 1 を書き込む
- [20, 30) を示す親階層 [2] の 「区間全体の最大高さ」 を、現在の値 0 と 1 の大きな方に置き換える
- [30, 100) を示す親階層 [3, 10) の 「区間全体の最大高さ」 を、現在の値 0 と 1 の大きな方に置き換える
- [30, 100) を示す親階層 [3, 10) の 「区間内すべてこの高さ以上」 を、現在の値 0 と 1 の大きな方に置き換える
- [26, 100) の最大高さを調べる → 0
- [7, 39) の区間を処理する
- [7, 39) の最大高さを調べる → 1
- [7, 10) の最大高さを、v 内の各高さと親階層の「区間内すべてこの高さ以上」の大きな方として得る → 0
- [10, 30) の最大高さを、親階層 [3, 10) の「区間全体の最大高さ」から得る → 1
- [30, 39) の最大高さを、v 内の各高さと親階層の「区間内すべてこの高さ以上」の大きな方として得る → 1
- [7, 39) の高さに 1 + 1 = 2 を入れる
- [7, 10) の最大高さに 2 を書き込む
- [7, 10) を示す親階層 [0] の 「区間全体の最大高さ」 を、現在の値 0 と 2 の大きな方に置き換える
- [10, 30) を示す親階層 [1, 3) の 「区間全体の最大高さ」 を、現在の値 0 と 2 の大きな方に置き換える
- [10, 30) を示す親階層 [1, 3) の 「区間内すべてこの高さ以上」 を、現在の値 0 と 2 の大きな方に置き換える
- [30, 39) の最大高さに 2 を書き込む
- [30, 39) を示す親階層 [0] の 「区間全体の最大高さ」 を、現在の値 1 と 2 の大きな方に置き換える
- [7, 39) の最大高さを調べる → 1
少し高速化しました。AC です。
コード
use num_integer::Roots;
use proconio::input;
use proconio::marker::Usize1;
struct Btree {
data: Vec<usize>,
up_size: usize,
up_data: Vec<usize>,
up_lazy: Vec<usize>,
}
impl Btree {
pub fn new(n: usize) -> Self {
let up_size = (n - 1).sqrt() + 1;
let data = vec![0; up_size * up_size];
let up_data = vec![0; up_size];
let up_lazy = vec![0; up_size];
Btree {
data,
up_size,
up_data,
up_lazy,
}
}
pub fn update(&mut self, l: usize, r: usize, x: usize) {
let n = self.up_size;
let mut l0 = l / n;
let r0 = r / n;
if l0 == r0 {
self.up_data[l0] = self.up_data[l0].max(x);
for i in l..r {
self.data[i] = x;
}
} else {
if l % n > 0 {
self.up_data[l0] = self.up_data[l0].max(x);
for i in l..((l0 + 1) * n) {
self.data[i] = x;
}
l0 += 1;
}
if l0 < r0 {
for i in l0..r0 {
self.up_data[i] = x;
self.up_lazy[i] = x;
}
}
if r % n > 0 {
self.up_data[r0] = self.up_data[r0].max(x);
for i in (r0 * n)..r {
self.data[i] = x;
}
}
}
}
pub fn prod(&mut self, l: usize, r: usize) -> usize {
let n = self.up_size;
let mut l0 = l / n;
let r0 = r / n;
let mut x = 0;
if l0 == r0 {
x = x.max(self.up_lazy[l0]);
x = x.max(*self.data[l..r].iter().max().unwrap());
} else {
if l % n > 0 {
x = x.max(self.up_lazy[l0]);
x = x.max(*self.data[l..((l0 + 1) * n)].iter().max().unwrap());
l0 += 1;
}
if l0 < r0 {
x = x.max(*self.up_data[l0..r0].iter().max().unwrap());
}
if r % n > 0 {
x = x.max(self.up_lazy[r0]);
x = x.max(*self.data[(r0 * n)..r].iter().max().unwrap());
}
}
x
}
}
fn main() {
input! {
w: usize,
lr: [(Usize1, Usize1)],
}
let mut t = Btree::new(w);
for &(l, r) in &lr {
let height = t.prod(l, r + 1) + 1;
t.update(l, r + 1, height);
println!("{}", height);
}
}
9. 遅延評価セグメント木を使用する
平方分割を入れ子にしたような形です。平方分割だと 100 個のコピーが発生するようなときも、セグメント木なら直接の子要素は 2 つだけで、高速に扱えます。
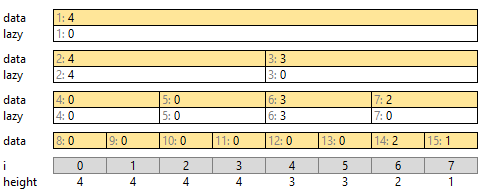
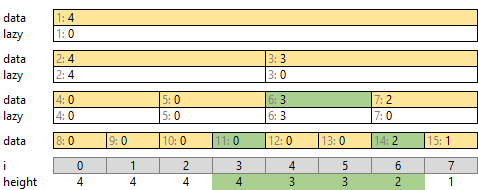
たとえばこのような形をしています。インデックスがどこから始まるか、遅延対象が同じ階層か一つ下かの違いで、同じ問題を解こうとしてもいろいろなセグメント木の作り方があります。本記事では平方分割と揃えます。
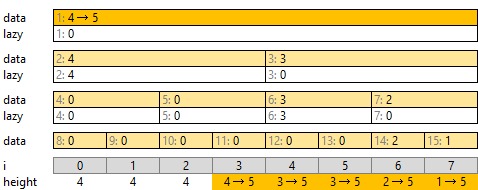
図では二分木のように描いています。data, lazy ともにコード上では一次元の配列として扱えます。各階層の最初のインデックスを 2 の累乗とします。
遅延セグメント木で区間の最大高さを得る
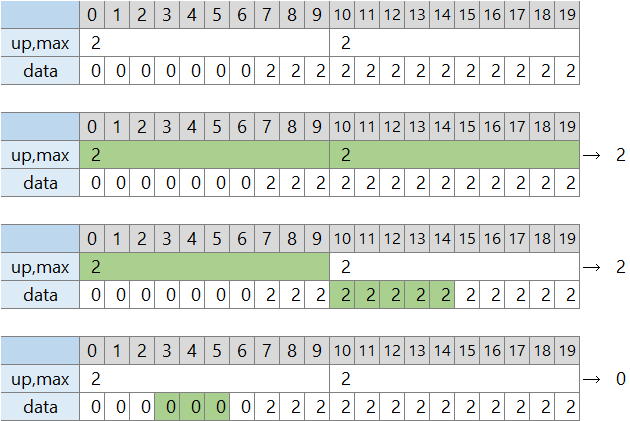
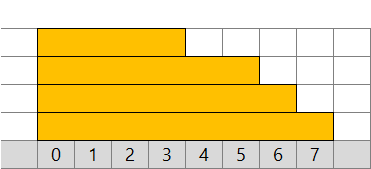
遅延成分がない場合は簡単です。緑の区間 [0, 6) 内の最大高さは、[0, 4) の最大高さと [4, 6) の最大高さのうち大きな方、4 です。
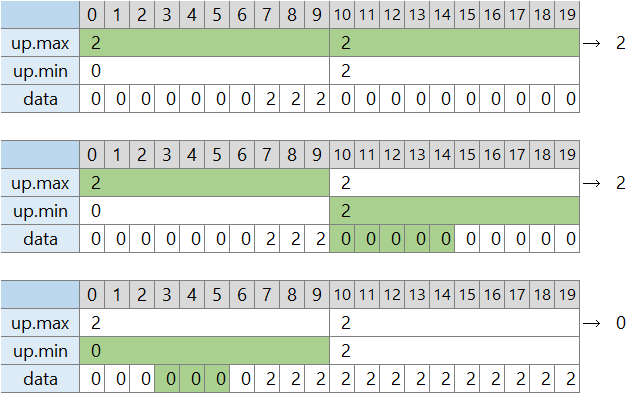
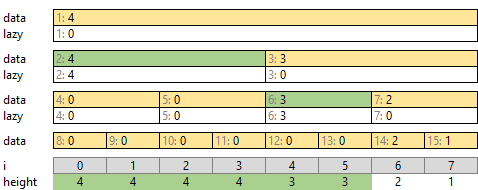
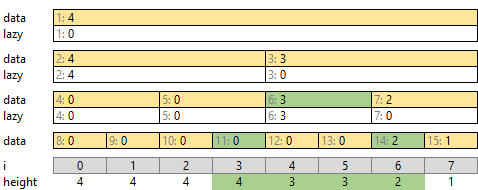
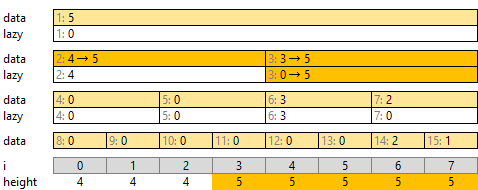
遅延成分がある場合は、必要な階層まで展開します。平方分割では 1 階層でした。セグメント木では繰り返します。たとえば区間 [3, 7) の最大高さを調べる場合を考えます。
区間の最大高さは [3] に入っている高さ 4 になるはずです。しかし [3] を見ても直接は高さが入っていません。一つ上の遅延成分にも入っていません。そこで、必要な時には値を配るようにします。
[3] の値に関する遅延成分があるか、上から辿って確認します。
[0, 8) は遅延成分がありません。次に進みます。 [0, 4), [4, 8) のうち、 [3] を含む左側 [0, 4) になります。
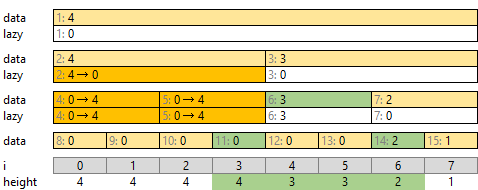
[0, 4) は遅延成分 4 があります。下の [0, 2), [2, 4) 両方に配り、「[0, 2), [2, 4) とも各座標の高さが 4 以上」とします。
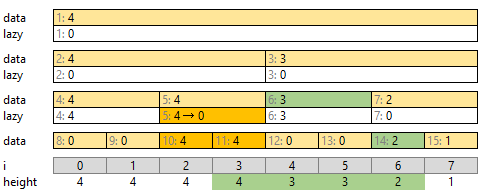
[2, 4) についても同様に、下の [2, 3), [3, 4) 両方に遅延成分 4 を配り、「[2, 3), [3, 4) とも各座標の高さが 4」とします。この末端には遅延成分がありません。高さ 4 で確定です。
右側 [4, 8) も同様に行います。こちらは関連する遅延成分がありません。遅延成分を配らなくて良いです。
こうしてそれぞれの緑の値が確定すれば、緑の場所の最大値を求めることで、区間 [3, 7) の最大値が求まります。
遅延セグメント木で区間の高さを更新する
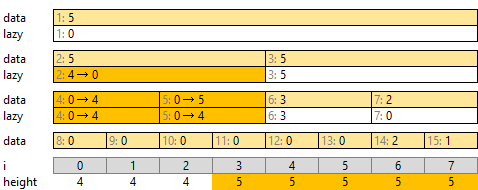
[3, 8) の区間を高さ 5 にすることを考えます。
まず、全体区間 [0, 8) の最大高さが 5 になります。一番上の data[1] を更新します。
つぎに半分に分けた [0, 4), [4, 8) を考えます。どちらも最大高さ 5 を入れます。また、右側 [4, 8) は下の高さがすべて 5 になりますので、 lazy[3] にも 5 を入れます。これで右側は終了です。
そのつぎに [0, 2), [2, 4) を考えます。どちらも data が 0 ですが、上の階層の lazy[2] によって高さ 4 が示されています。これを両方に配り、「[0, 2), [2, 4) とも各座標の高さが 4 以上」とします。ただし [3, 8) の高さは 5 でしたので、[3, 4) の最大高さも 5 となります。
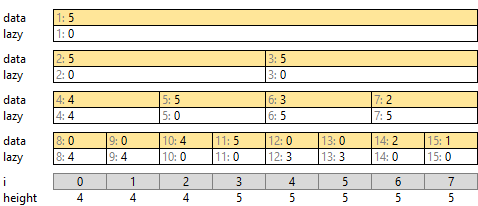
最後に [0, 2), [2, 4) のうち [3, 8) と区間が重なっている [2, 4) を、同様に処理します。末端には遅延成分がありません。 [2, 3), [3, 4) の data だけ更新します。
こうして区間を更新できました。
9-A. 遅延セグメント木を書いて解く (AC)
上記をそのまま実装すれば良いです。実装量が多く難しかったので、公式解答例を参考に書きました。 AC です。
コード
use proconio::input;
use proconio::marker::Usize1;
struct LazySegTree {
size: usize,
data: Vec<usize>,
lazy: Vec<usize>,
}
impl LazySegTree {
fn push(&mut self, k: usize) {
let lazy = self.lazy[k];
if lazy == 0 {
return;
}
self.data[k * 2] = self.data[k * 2].max(lazy);
self.data[k * 2 + 1] = self.data[k * 2 + 1].max(lazy);
if k * 2 < self.size {
self.lazy[k * 2] = self.lazy[k * 2].max(lazy);
self.lazy[k * 2 + 1] = self.lazy[k * 2 + 1].max(lazy);
}
self.lazy[k] = 0;
}
fn update_impl(&mut self, lr: (usize, usize), x: usize, k: usize, lr0: (usize, usize)) {
let (l, r) = lr;
let (l0, r0) = lr0;
if r0 <= l || r <= l0 {
// noop
} else if l <= l0 && r0 <= r {
self.data[k] = self.data[k].max(x);
if k < self.size {
self.lazy[k] = self.lazy[k].max(x);
}
} else {
self.push(k);
self.update_impl(lr, x, k * 2, (l0, (l0 + r0) / 2));
self.update_impl(lr, x, k * 2 + 1, ((l0 + r0) / 2, r0));
self.data[k] = self.data[k * 2].max(self.data[k * 2 + 1]);
}
}
fn prod_impl(&mut self, lr: (usize, usize), k: usize, lr0: (usize, usize)) -> usize {
let (l, r) = lr;
let (l0, r0) = lr0;
if r0 <= l || r <= l0 {
0
} else if l <= l0 && r0 <= r {
self.data[k]
} else {
self.push(k);
let l_val = self.prod_impl(lr, k * 2, (l0, (l0 + r0) / 2));
let r_val = self.prod_impl(lr, k * 2 + 1, ((l0 + r0) / 2, r0));
l_val.max(r_val)
}
}
pub fn new(n: usize) -> Self {
let ceil_pow2 = 32 - ((n as u32) - 1).leading_zeros();
let size = 1 << ceil_pow2;
let data = vec![0; size * 2];
let lazy = vec![0; size];
LazySegTree { size, data, lazy }
}
pub fn update(&mut self, l: usize, r: usize, x: usize) {
self.update_impl((l, r), x, 1, (0, self.size));
}
pub fn prod(&mut self, l: usize, r: usize) -> usize {
self.prod_impl((l, r), 1, (0, self.size))
}
}
fn main() {
input! {
w: usize,
lr: [(Usize1, Usize1)],
}
let mut seg = LazySegTree::new(w);
for &(l, r) in &lr {
let height = seg.prod(l, r + 1) + 1;
seg.update(l, r + 1, height);
println!("{}", height);
}
}
9-B. 遅延セグメント木を同階層を見るように変える (AC)
先ほどは「高さは data と、1 つ上の階層の遅延成分のうち大きな方」でした。公式解答例は「同じ階層の遅延成分のうち大きな方」となっています。
遅延成分を持つ量が増えます。その分場合分けが減り、より単純な実装になります。
コード
use proconio::input;
use proconio::marker::Usize1;
struct LazySegTree {
size: usize,
data: Vec<usize>,
lazy: Vec<usize>,
}
impl LazySegTree {
fn push(&mut self, k: usize) {
let lazy = self.lazy[k];
if k < self.size {
self.lazy[k * 2] = self.lazy[k * 2].max(lazy);
self.lazy[k * 2 + 1] = self.lazy[k * 2 + 1].max(lazy);
}
self.data[k] = self.data[k].max(lazy);
self.lazy[k] = 0;
}
fn update_impl(&mut self, lr: (usize, usize), x: usize, k: usize, lr0: (usize, usize)) {
self.push(k);
let (l, r) = lr;
let (l0, r0) = lr0;
if r0 <= l || r <= l0 {
// noop
} else if l <= l0 && r0 <= r {
self.lazy[k] = x;
self.push(k);
} else {
self.update_impl(lr, x, k * 2, (l0, (l0 + r0) / 2));
self.update_impl(lr, x, k * 2 + 1, ((l0 + r0) / 2, r0));
self.data[k] = self.data[k * 2].max(self.data[k * 2 + 1]);
}
}
fn prod_impl(&mut self, lr: (usize, usize), k: usize, lr0: (usize, usize)) -> usize {
self.push(k);
let (l, r) = lr;
let (l0, r0) = lr0;
if r0 <= l || r <= l0 {
0
} else if l <= l0 && r0 <= r {
self.data[k]
} else {
let l_val = self.prod_impl(lr, k * 2, (l0, (l0 + r0) / 2));
let r_val = self.prod_impl(lr, k * 2 + 1, ((l0 + r0) / 2, r0));
l_val.max(r_val)
}
}
pub fn new(n: usize) -> Self {
let ceil_pow2 = 32 - ((n as u32) - 1).leading_zeros();
let size = 1 << ceil_pow2;
let data = vec![0; size * 2];
let lazy = vec![0; size * 2];
LazySegTree { size, data, lazy }
}
pub fn update(&mut self, l: usize, r: usize, x: usize) {
self.update_impl((l, r), x, 1, (0, self.size));
}
pub fn prod(&mut self, l: usize, r: usize) -> usize {
self.prod_impl((l, r), 1, (0, self.size))
}
}
fn main() {
input! {
w: usize,
lr: [(Usize1, Usize1)],
}
let mut seg = LazySegTree::new(w);
for &(l, r) in &lr {
let height = seg.prod(l, r + 1) + 1;
seg.update(l, r + 1, height);
println!("{}", height);
}
}
9-C. 遅延セグメント木で値のばらまきをやめる (AC)
「8-B. 平方分割 + 「高さがこれ以上」補助情報」では補助情報を下階層に配っていませんでした。セグメント木でも同様に、高さを「対応する data と、自分より上の階層にあるすべての lazy のうち大きな方」とすれば良いです。
たとえば [3] の高さは、自身の高さ 5 と、上にある lazy [1, 4, 4] すべての中の最大値となります。
遅延セグメント木というよりは、2 つのセグメント木を組み合わせた特殊形と言えそうです。
コード
use proconio::input;
use proconio::marker::Usize1;
struct LazySegTree {
size: usize,
data: Vec<usize>,
lazy: Vec<usize>,
}
impl LazySegTree {
fn update_impl(
&mut self,
lr: (usize, usize),
x: usize,
k: usize,
lr0: (usize, usize),
lazy: usize,
) {
let (l, r) = lr;
let (l0, r0) = lr0;
if r0 <= l || r <= l0 {
// noop
} else if l <= l0 && r0 <= r {
self.data[k] = self.data[k].max(x);
if k < self.size {
self.lazy[k] = self.lazy[k].max(x);
}
} else {
let lazy = lazy.max(self.lazy[k]);
self.update_impl(lr, x, k * 2, (l0, (l0 + r0) / 2), lazy);
self.update_impl(lr, x, k * 2 + 1, ((l0 + r0) / 2, r0), lazy);
self.data[k] = self.data[k * 2].max(self.data[k * 2 + 1]);
}
}
fn prod_impl(
&mut self,
lr: (usize, usize),
k: usize,
lr0: (usize, usize),
lazy: usize,
) -> usize {
let (l, r) = lr;
let (l0, r0) = lr0;
if r0 <= l || r <= l0 {
0
} else if l <= l0 && r0 <= r {
lazy.max(self.data[k])
} else {
let lazy = lazy.max(self.lazy[k]);
let l_val = self.prod_impl(lr, k * 2, (l0, (l0 + r0) / 2), lazy);
let r_val = self.prod_impl(lr, k * 2 + 1, ((l0 + r0) / 2, r0), lazy);
l_val.max(r_val)
}
}
pub fn new(n: usize) -> Self {
let ceil_pow2 = 32 - ((n as u32) - 1).leading_zeros();
let size = 1 << ceil_pow2;
let data = vec![0; size * 2];
let lazy = vec![0; size];
LazySegTree { size, data, lazy }
}
pub fn update(&mut self, l: usize, r: usize, x: usize) {
self.update_impl((l, r), x, 1, (0, self.size), 0);
}
pub fn prod(&mut self, l: usize, r: usize) -> usize {
self.prod_impl((l, r), 1, (0, self.size), 0)
}
}
fn main() {
input! {
w: usize,
lr: [(Usize1, Usize1)],
}
let mut seg = LazySegTree::new(w);
for &(l, r) in &lr {
let height = seg.prod(l, r + 1) + 1;
seg.update(l, r + 1, height);
println!("{}", height);
}
}
9-D. AtCoder Library を使う (AC)
「遅延セグメント木を書いて解く」で考え方は分かっても、競技プログラミングで制限時間がある中、遅延セグメント木を書くのは大変です。
過去問で解いたことがある場合は、コピーペーストである程度使いまわしできるかもしれません。それでも書き換え箇所が多くなりかねません。上の実装では .max() が何度も現れていました。
そういう時にはライブラリー。 Rust では ac-library-rs を使えます。
ライブラリーを使えるように準備します。
- github からリポジトリーを clone する
- Python をインストール
ライブラリーから LazySegtree をコピーペーストできる形で取り出します。C++ はサーバー側にライブラリーがありますので #include だけで使えます。Rust は 2022 年 9 月時点ではそうなっていません。
-
python .\expand.py lazysegtree- ターミナルにコピーペーストできるコードが出力される
- (lazysegtree は長いので
python .\expand.py lazysegtree > work.rsのようにファイル出力をおすすめ)
- まるっと貼り付ける
次に LazySegtree の構造体を定義します。
| 設定するもの | 意味 | 設定方法 |
|---|---|---|
M |
data の処理方法を表す型 | Max<usize> |
F |
遅延成分の型 | usize |
identity_map() -> F |
遅延成分のなにも作用しない値 | 0 |
mapping(&f: F, &x: M::S) -> M::S |
遅延成分を下の data に適用する方法 | max() |
composition(&f: F, &g: F) -> F |
遅延成分を下の遅延成分と混ぜる方法 | max() |
M が遅延なしのセグメント木でも使うデータ構造です。「区間の高さは各座標の高さの最大値」のようによく使うものは、Max<usize> のように簡単に使えるようになっています。
mapping と composition に何を入れれば良いかは、引数と返の型が物語っています。
「セグメント木に乗せる」 方法だけ書けば、あとはライブラリーが行ってくれます。今までの苦労はなんだったのだろうという勢いです。
コード (書いたもの)
use proconio::{input, marker::Usize1};
type M = Max<usize>;
struct F;
impl MapMonoid for F {
type M = M;
type F = usize;
fn identity_map() -> Self::F {
0
}
fn mapping(&f: &Self::F, &x: &<M as Monoid>::S) -> <M as Monoid>::S {
f.max(x)
}
fn composition(&f: &Self::F, &g: &Self::F) -> Self::F {
f.max(g)
}
}
fn main() {
input! {
w: usize,
lr: [(Usize1, Usize1)],
}
let mut segtree = LazySegtree::<F>::new(w);
for &(l, r) in &lr {
let height = segtree.prod(l, r + 1) + 1;
segtree.apply_range(l, r + 1, height);
println!("{}", height);
}
}
コード (AtCoder Library からコピーペースト)
//https://github.com/rust-lang-ja/ac-library-rs
pub mod internal_bit {
// Skipped:
//
// - `bsf` = `__builtin_ctz`: is equivalent to `{integer}::trailing_zeros`
#[allow(dead_code)]
pub(crate) fn ceil_pow2(n: u32) -> u32 {
32 - n.saturating_sub(1).leading_zeros()
}
#[cfg(test)]
mod tests {
#[test]
fn ceil_pow2() {
// https://github.com/atcoder/ac-library/blob/2088c8e2431c3f4d29a2cfabc6529fe0a0586c48/test/unittest/bit_test.cpp
assert_eq!(0, super::ceil_pow2(0));
assert_eq!(0, super::ceil_pow2(1));
assert_eq!(1, super::ceil_pow2(2));
assert_eq!(2, super::ceil_pow2(3));
assert_eq!(2, super::ceil_pow2(4));
assert_eq!(3, super::ceil_pow2(5));
assert_eq!(3, super::ceil_pow2(6));
assert_eq!(3, super::ceil_pow2(7));
assert_eq!(3, super::ceil_pow2(8));
assert_eq!(4, super::ceil_pow2(9));
assert_eq!(30, super::ceil_pow2(1 << 30));
assert_eq!(31, super::ceil_pow2((1 << 30) + 1));
assert_eq!(32, super::ceil_pow2(u32::max_value()));
}
}
}
pub mod internal_type_traits {
use std::{
fmt,
iter::{Product, Sum},
ops::{
Add, AddAssign, BitAnd, BitAndAssign, BitOr, BitOrAssign, BitXor, BitXorAssign, Div,
DivAssign, Mul, MulAssign, Not, Rem, RemAssign, Shl, ShlAssign, Shr, ShrAssign, Sub,
SubAssign,
},
};
// Skipped:
//
// - `is_signed_int_t<T>` (probably won't be used directly in `modint.rs`)
// - `is_unsigned_int_t<T>` (probably won't be used directly in `modint.rs`)
// - `to_unsigned_t<T>` (not used in `fenwicktree.rs`)
/// Corresponds to `std::is_integral` in C++.
// We will remove unnecessary bounds later.
//
// Maybe we should rename this to `PrimitiveInteger` or something, as it probably won't be used in the
// same way as the original ACL.
pub trait Integral:
'static
+ Send
+ Sync
+ Copy
+ Ord
+ Not<Output = Self>
+ Add<Output = Self>
+ Sub<Output = Self>
+ Mul<Output = Self>
+ Div<Output = Self>
+ Rem<Output = Self>
+ AddAssign
+ SubAssign
+ MulAssign
+ DivAssign
+ RemAssign
+ Sum
+ Product
+ BitOr<Output = Self>
+ BitAnd<Output = Self>
+ BitXor<Output = Self>
+ BitOrAssign
+ BitAndAssign
+ BitXorAssign
+ Shl<Output = Self>
+ Shr<Output = Self>
+ ShlAssign
+ ShrAssign
+ fmt::Display
+ fmt::Debug
+ fmt::Binary
+ fmt::Octal
+ Zero
+ One
+ BoundedBelow
+ BoundedAbove
{
}
/// Class that has additive identity element
pub trait Zero {
/// The additive identity element
fn zero() -> Self;
}
/// Class that has multiplicative identity element
pub trait One {
/// The multiplicative identity element
fn one() -> Self;
}
pub trait BoundedBelow {
fn min_value() -> Self;
}
pub trait BoundedAbove {
fn max_value() -> Self;
}
macro_rules! impl_integral {
($($ty:ty),*) => {
$(
impl Zero for $ty {
#[inline]
fn zero() -> Self {
0
}
}
impl One for $ty {
#[inline]
fn one() -> Self {
1
}
}
impl BoundedBelow for $ty {
#[inline]
fn min_value() -> Self {
Self::min_value()
}
}
impl BoundedAbove for $ty {
#[inline]
fn max_value() -> Self {
Self::max_value()
}
}
impl Integral for $ty {}
)*
};
}
impl_integral!(i8, i16, i32, i64, i128, isize, u8, u16, u32, u64, u128, usize);
}
pub mod lazysegtree {
use crate::internal_bit::ceil_pow2;
use crate::Monoid;
pub trait MapMonoid {
type M: Monoid;
type F: Clone;
// type S = <Self::M as Monoid>::S;
fn identity_element() -> <Self::M as Monoid>::S {
Self::M::identity()
}
fn binary_operation(
a: &<Self::M as Monoid>::S,
b: &<Self::M as Monoid>::S,
) -> <Self::M as Monoid>::S {
Self::M::binary_operation(a, b)
}
fn identity_map() -> Self::F;
fn mapping(f: &Self::F, x: &<Self::M as Monoid>::S) -> <Self::M as Monoid>::S;
fn composition(f: &Self::F, g: &Self::F) -> Self::F;
}
impl<F: MapMonoid> Default for LazySegtree<F> {
fn default() -> Self {
Self::new(0)
}
}
impl<F: MapMonoid> LazySegtree<F> {
pub fn new(n: usize) -> Self {
vec![F::identity_element(); n].into()
}
}
impl<F: MapMonoid> From<Vec<<F::M as Monoid>::S>> for LazySegtree<F> {
fn from(v: Vec<<F::M as Monoid>::S>) -> Self {
let n = v.len();
let log = ceil_pow2(n as u32) as usize;
let size = 1 << log;
let mut d = vec![F::identity_element(); 2 * size];
let lz = vec![F::identity_map(); size];
d[size..(size + n)].clone_from_slice(&v);
let mut ret = LazySegtree {
n,
size,
log,
d,
lz,
};
for i in (1..size).rev() {
ret.update(i);
}
ret
}
}
impl<F: MapMonoid> LazySegtree<F> {
pub fn set(&mut self, mut p: usize, x: <F::M as Monoid>::S) {
assert!(p < self.n);
p += self.size;
for i in (1..=self.log).rev() {
self.push(p >> i);
}
self.d[p] = x;
for i in 1..=self.log {
self.update(p >> i);
}
}
pub fn get(&mut self, mut p: usize) -> <F::M as Monoid>::S {
assert!(p < self.n);
p += self.size;
for i in (1..=self.log).rev() {
self.push(p >> i);
}
self.d[p].clone()
}
pub fn prod(&mut self, mut l: usize, mut r: usize) -> <F::M as Monoid>::S {
assert!(l <= r && r <= self.n);
if l == r {
return F::identity_element();
}
l += self.size;
r += self.size;
for i in (1..=self.log).rev() {
if ((l >> i) << i) != l {
self.push(l >> i);
}
if ((r >> i) << i) != r {
self.push(r >> i);
}
}
let mut sml = F::identity_element();
let mut smr = F::identity_element();
while l < r {
if l & 1 != 0 {
sml = F::binary_operation(&sml, &self.d[l]);
l += 1;
}
if r & 1 != 0 {
r -= 1;
smr = F::binary_operation(&self.d[r], &smr);
}
l >>= 1;
r >>= 1;
}
F::binary_operation(&sml, &smr)
}
pub fn all_prod(&self) -> <F::M as Monoid>::S {
self.d[1].clone()
}
pub fn apply(&mut self, mut p: usize, f: F::F) {
assert!(p < self.n);
p += self.size;
for i in (1..=self.log).rev() {
self.push(p >> i);
}
self.d[p] = F::mapping(&f, &self.d[p]);
for i in 1..=self.log {
self.update(p >> i);
}
}
pub fn apply_range(&mut self, mut l: usize, mut r: usize, f: F::F) {
assert!(l <= r && r <= self.n);
if l == r {
return;
}
l += self.size;
r += self.size;
for i in (1..=self.log).rev() {
if ((l >> i) << i) != l {
self.push(l >> i);
}
if ((r >> i) << i) != r {
self.push((r - 1) >> i);
}
}
{
let l2 = l;
let r2 = r;
while l < r {
if l & 1 != 0 {
self.all_apply(l, f.clone());
l += 1;
}
if r & 1 != 0 {
r -= 1;
self.all_apply(r, f.clone());
}
l >>= 1;
r >>= 1;
}
l = l2;
r = r2;
}
for i in 1..=self.log {
if ((l >> i) << i) != l {
self.update(l >> i);
}
if ((r >> i) << i) != r {
self.update((r - 1) >> i);
}
}
}
pub fn max_right<G>(&mut self, mut l: usize, g: G) -> usize
where
G: Fn(<F::M as Monoid>::S) -> bool,
{
assert!(l <= self.n);
assert!(g(F::identity_element()));
if l == self.n {
return self.n;
}
l += self.size;
for i in (1..=self.log).rev() {
self.push(l >> i);
}
let mut sm = F::identity_element();
while {
// do
while l % 2 == 0 {
l >>= 1;
}
if !g(F::binary_operation(&sm, &self.d[l])) {
while l < self.size {
self.push(l);
l *= 2;
let res = F::binary_operation(&sm, &self.d[l]);
if g(res.clone()) {
sm = res;
l += 1;
}
}
return l - self.size;
}
sm = F::binary_operation(&sm, &self.d[l]);
l += 1;
//while
{
let l = l as isize;
(l & -l) != l
}
} {}
self.n
}
pub fn min_left<G>(&mut self, mut r: usize, g: G) -> usize
where
G: Fn(<F::M as Monoid>::S) -> bool,
{
assert!(r <= self.n);
assert!(g(F::identity_element()));
if r == 0 {
return 0;
}
r += self.size;
for i in (1..=self.log).rev() {
self.push((r - 1) >> i);
}
let mut sm = F::identity_element();
while {
// do
r -= 1;
while r > 1 && r % 2 != 0 {
r >>= 1;
}
if !g(F::binary_operation(&self.d[r], &sm)) {
while r < self.size {
self.push(r);
r = 2 * r + 1;
let res = F::binary_operation(&self.d[r], &sm);
if g(res.clone()) {
sm = res;
r -= 1;
}
}
return r + 1 - self.size;
}
sm = F::binary_operation(&self.d[r], &sm);
// while
{
let r = r as isize;
(r & -r) != r
}
} {}
0
}
}
pub struct LazySegtree<F>
where
F: MapMonoid,
{
n: usize,
size: usize,
log: usize,
d: Vec<<F::M as Monoid>::S>,
lz: Vec<F::F>,
}
impl<F> LazySegtree<F>
where
F: MapMonoid,
{
fn update(&mut self, k: usize) {
self.d[k] = F::binary_operation(&self.d[2 * k], &self.d[2 * k + 1]);
}
fn all_apply(&mut self, k: usize, f: F::F) {
self.d[k] = F::mapping(&f, &self.d[k]);
if k < self.size {
self.lz[k] = F::composition(&f, &self.lz[k]);
}
}
fn push(&mut self, k: usize) {
self.all_apply(2 * k, self.lz[k].clone());
self.all_apply(2 * k + 1, self.lz[k].clone());
self.lz[k] = F::identity_map();
}
}
// TODO is it useful?
use std::fmt::{Debug, Error, Formatter, Write};
impl<F> Debug for LazySegtree<F>
where
F: MapMonoid,
F::F: Debug,
<F::M as Monoid>::S: Debug,
{
fn fmt(&self, f: &mut Formatter<'_>) -> Result<(), Error> {
for i in 0..self.log {
for j in 0..1 << i {
f.write_fmt(format_args!(
"{:?}[{:?}]\t",
self.d[(1 << i) + j],
self.lz[(1 << i) + j]
))?;
}
f.write_char('\n')?;
}
for i in 0..self.size {
f.write_fmt(format_args!("{:?}\t", self.d[self.size + i]))?;
}
Ok(())
}
}
#[cfg(test)]
mod tests {
use crate::{LazySegtree, MapMonoid, Max};
struct MaxAdd;
impl MapMonoid for MaxAdd {
type M = Max<i32>;
type F = i32;
fn identity_map() -> Self::F {
0
}
fn mapping(&f: &i32, &x: &i32) -> i32 {
f + x
}
fn composition(&f: &i32, &g: &i32) -> i32 {
f + g
}
}
#[test]
fn test_max_add_lazy_segtree() {
let base = vec![3, 1, 4, 1, 5, 9, 2, 6, 5, 3];
let n = base.len();
let mut segtree: LazySegtree<MaxAdd> = base.clone().into();
check_segtree(&base, &mut segtree);
let mut segtree = LazySegtree::<MaxAdd>::new(n);
let mut internal = vec![i32::min_value(); n];
for i in 0..n {
segtree.set(i, base[i]);
internal[i] = base[i];
check_segtree(&internal, &mut segtree);
}
segtree.set(6, 5);
internal[6] = 5;
check_segtree(&internal, &mut segtree);
segtree.apply(5, 1);
internal[5] += 1;
check_segtree(&internal, &mut segtree);
segtree.set(6, 0);
internal[6] = 0;
check_segtree(&internal, &mut segtree);
segtree.apply_range(3, 8, 2);
internal[3..8].iter_mut().for_each(|e| *e += 2);
check_segtree(&internal, &mut segtree);
}
//noinspection DuplicatedCode
fn check_segtree(base: &[i32], segtree: &mut LazySegtree<MaxAdd>) {
let n = base.len();
#[allow(clippy::needless_range_loop)]
for i in 0..n {
assert_eq!(segtree.get(i), base[i]);
}
for i in 0..=n {
for j in i..=n {
assert_eq!(
segtree.prod(i, j),
base[i..j].iter().max().copied().unwrap_or(i32::min_value())
);
}
}
assert_eq!(
segtree.all_prod(),
base.iter().max().copied().unwrap_or(i32::min_value())
);
for k in 0..=10 {
let f = |x| x < k;
for i in 0..=n {
assert_eq!(
Some(segtree.max_right(i, f)),
(i..=n)
.filter(|&j| f(base[i..j]
.iter()
.max()
.copied()
.unwrap_or(i32::min_value())))
.max()
);
}
for j in 0..=n {
assert_eq!(
Some(segtree.min_left(j, f)),
(0..=j)
.filter(|&i| f(base[i..j]
.iter()
.max()
.copied()
.unwrap_or(i32::min_value())))
.min()
);
}
}
}
}
}
pub mod segtree {
use crate::internal_bit::ceil_pow2;
use crate::internal_type_traits::{BoundedAbove, BoundedBelow, One, Zero};
use std::cmp::{max, min};
use std::convert::Infallible;
use std::marker::PhantomData;
use std::ops::{Add, Mul};
// TODO Should I split monoid-related traits to another module?
pub trait Monoid {
type S: Clone;
fn identity() -> Self::S;
fn binary_operation(a: &Self::S, b: &Self::S) -> Self::S;
}
pub struct Max<S>(Infallible, PhantomData<fn() -> S>);
impl<S> Monoid for Max<S>
where
S: Copy + Ord + BoundedBelow,
{
type S = S;
fn identity() -> Self::S {
S::min_value()
}
fn binary_operation(a: &Self::S, b: &Self::S) -> Self::S {
max(*a, *b)
}
}
pub struct Min<S>(Infallible, PhantomData<fn() -> S>);
impl<S> Monoid for Min<S>
where
S: Copy + Ord + BoundedAbove,
{
type S = S;
fn identity() -> Self::S {
S::max_value()
}
fn binary_operation(a: &Self::S, b: &Self::S) -> Self::S {
min(*a, *b)
}
}
pub struct Additive<S>(Infallible, PhantomData<fn() -> S>);
impl<S> Monoid for Additive<S>
where
S: Copy + Add<Output = S> + Zero,
{
type S = S;
fn identity() -> Self::S {
S::zero()
}
fn binary_operation(a: &Self::S, b: &Self::S) -> Self::S {
*a + *b
}
}
pub struct Multiplicative<S>(Infallible, PhantomData<fn() -> S>);
impl<S> Monoid for Multiplicative<S>
where
S: Copy + Mul<Output = S> + One,
{
type S = S;
fn identity() -> Self::S {
S::one()
}
fn binary_operation(a: &Self::S, b: &Self::S) -> Self::S {
*a * *b
}
}
impl<M: Monoid> Default for Segtree<M> {
fn default() -> Self {
Segtree::new(0)
}
}
impl<M: Monoid> Segtree<M> {
pub fn new(n: usize) -> Segtree<M> {
vec![M::identity(); n].into()
}
}
impl<M: Monoid> From<Vec<M::S>> for Segtree<M> {
fn from(v: Vec<M::S>) -> Self {
let n = v.len();
let log = ceil_pow2(n as u32) as usize;
let size = 1 << log;
let mut d = vec![M::identity(); 2 * size];
d[size..(size + n)].clone_from_slice(&v);
let mut ret = Segtree { n, size, log, d };
for i in (1..size).rev() {
ret.update(i);
}
ret
}
}
impl<M: Monoid> Segtree<M> {
pub fn set(&mut self, mut p: usize, x: M::S) {
assert!(p < self.n);
p += self.size;
self.d[p] = x;
for i in 1..=self.log {
self.update(p >> i);
}
}
pub fn get(&self, p: usize) -> M::S {
assert!(p < self.n);
self.d[p + self.size].clone()
}
pub fn prod(&self, mut l: usize, mut r: usize) -> M::S {
assert!(l <= r && r <= self.n);
let mut sml = M::identity();
let mut smr = M::identity();
l += self.size;
r += self.size;
while l < r {
if l & 1 != 0 {
sml = M::binary_operation(&sml, &self.d[l]);
l += 1;
}
if r & 1 != 0 {
r -= 1;
smr = M::binary_operation(&self.d[r], &smr);
}
l >>= 1;
r >>= 1;
}
M::binary_operation(&sml, &smr)
}
pub fn all_prod(&self) -> M::S {
self.d[1].clone()
}
pub fn max_right<F>(&self, mut l: usize, f: F) -> usize
where
F: Fn(&M::S) -> bool,
{
assert!(l <= self.n);
assert!(f(&M::identity()));
if l == self.n {
return self.n;
}
l += self.size;
let mut sm = M::identity();
while {
// do
while l % 2 == 0 {
l >>= 1;
}
if !f(&M::binary_operation(&sm, &self.d[l])) {
while l < self.size {
l *= 2;
let res = M::binary_operation(&sm, &self.d[l]);
if f(&res) {
sm = res;
l += 1;
}
}
return l - self.size;
}
sm = M::binary_operation(&sm, &self.d[l]);
l += 1;
// while
{
let l = l as isize;
(l & -l) != l
}
} {}
self.n
}
pub fn min_left<F>(&self, mut r: usize, f: F) -> usize
where
F: Fn(&M::S) -> bool,
{
assert!(r <= self.n);
assert!(f(&M::identity()));
if r == 0 {
return 0;
}
r += self.size;
let mut sm = M::identity();
while {
// do
r -= 1;
while r > 1 && r % 2 == 1 {
r >>= 1;
}
if !f(&M::binary_operation(&self.d[r], &sm)) {
while r < self.size {
r = 2 * r + 1;
let res = M::binary_operation(&self.d[r], &sm);
if f(&res) {
sm = res;
r -= 1;
}
}
return r + 1 - self.size;
}
sm = M::binary_operation(&self.d[r], &sm);
// while
{
let r = r as isize;
(r & -r) != r
}
} {}
0
}
fn update(&mut self, k: usize) {
self.d[k] = M::binary_operation(&self.d[2 * k], &self.d[2 * k + 1]);
}
}
// Maybe we can use this someday
// ```
// for i in 0..=self.log {
// for j in 0..1 << i {
// print!("{}\t", self.d[(1 << i) + j]);
// }
// println!();
// }
// ```
pub struct Segtree<M>
where
M: Monoid,
{
// variable name is _n in original library
n: usize,
size: usize,
log: usize,
d: Vec<M::S>,
}
#[cfg(test)]
mod tests {
use crate::segtree::Max;
use crate::Segtree;
#[test]
fn test_max_segtree() {
let base = vec![3, 1, 4, 1, 5, 9, 2, 6, 5, 3];
let n = base.len();
let segtree: Segtree<Max<_>> = base.clone().into();
check_segtree(&base, &segtree);
let mut segtree = Segtree::<Max<_>>::new(n);
let mut internal = vec![i32::min_value(); n];
for i in 0..n {
segtree.set(i, base[i]);
internal[i] = base[i];
check_segtree(&internal, &segtree);
}
segtree.set(6, 5);
internal[6] = 5;
check_segtree(&internal, &segtree);
segtree.set(6, 0);
internal[6] = 0;
check_segtree(&internal, &segtree);
}
//noinspection DuplicatedCode
fn check_segtree(base: &[i32], segtree: &Segtree<Max<i32>>) {
let n = base.len();
#[allow(clippy::needless_range_loop)]
for i in 0..n {
assert_eq!(segtree.get(i), base[i]);
}
for i in 0..=n {
for j in i..=n {
assert_eq!(
segtree.prod(i, j),
base[i..j].iter().max().copied().unwrap_or(i32::min_value())
);
}
}
assert_eq!(
segtree.all_prod(),
base.iter().max().copied().unwrap_or(i32::min_value())
);
for k in 0..=10 {
let f = |&x: &i32| x < k;
for i in 0..=n {
assert_eq!(
Some(segtree.max_right(i, f)),
(i..=n)
.filter(|&j| f(&base[i..j]
.iter()
.max()
.copied()
.unwrap_or(i32::min_value())))
.max()
);
}
for j in 0..=n {
assert_eq!(
Some(segtree.min_left(j, f)),
(0..=j)
.filter(|&i| f(&base[i..j]
.iter()
.max()
.copied()
.unwrap_or(i32::min_value())))
.min()
);
}
}
}
}
}
use lazysegtree::*;
use segtree::*;
最後に
9 通りのデータ構造を使い、細かな派生を含めたコードを書きました。TLE 4 個、AC 10 個貼り付けていました。記事を書いているうちに膨れました。
競技プログラミング中は「区間更新なら遅延評価セグメント木」でだいたい大丈夫だと思います。他にもいろいろなアルゴリズムがあり、いろいろな解き方ができる。遅延評価セグメント木を使う場合もその中でいろいろな当てはめ方ができる 6、というところが伝われば満足です。
最後に、楽しい問題を作成した E869120 さん、常設コンテストとして解答投稿環境を用意している AtCoder 運営に感謝して、本記事を終わります。
参考リンク
- 全般
- フェニック木
- Binary indexed tree HCPC: 北海道大学競技プログラミングサークル 発表資料
- std::setを使わない代替テクニック [いかたこのたこつぼ]
- 平方分割
- セグメント木
-
競技プログラミングでは、配列のインデックスが 0 開始のプログラミング言語で、1 開始の入力を扱うことがよくあります。入力データに寄せて配列の [0] を使わないようにする、入力データ側を 1減らして配列の [0] から埋めるようにする、どちらもアリです。本記事中では後者にしています。 Rust では proconio - Rust の Usize1 型を指定すると、入力データを -1 して読み込みます。 ↩
-
Rust で配列内に昇順に並んだ値を二分探索する場合は、
superslice::Extが便利です ↩ -
後ろ方向の挿入が遅いです。前方向にも配列領域を確保して、挿入時に両端どちらに近いかで処理を切り替えればもしかすると通るかもしれません。Rust で行おうとすると、VecDeque に区間挿入のインターフェースがなく、 unsafe な世界なしには手間そうです。C++ の deque ならもしかすると。 ↩
-
[0, 1), [2, 3), [1, 2) の順に高さを増やしたときに、v の中身が [1, 1, 1] と同じ値が連続する、すこし無駄のある実装です。でも速度に与える影響は誤差程度です。 ↩
-
直接フェニック木を使うのではなく、フェニック木を使った
FenwickTreeSetにしました。フェニック木ではインデックス 1 開始という事情を、ここでインデックス 0 開始でも使えるようにしています。ルールが変わる場所を決めておくと、不具合混入を避けやすいです。 ↩ -
遅延評価セグメント木は自由度が高いです。丁寧な遅延評価セグメント木の解説サイトはたくさんありますが、それぞれが微妙に異なった見方をしていて、そのために「何が正しいのだろう……」と混乱していました。「適用方針も実装方針もいろいろあるけれど、基本は二分木」と思ってからは、あまり怖くなくなりました。 ↩