bow-tie構造解析

Bow-tie構造とは

有効ネットワークにおいて、Bow-tie構造とは強連結成分（SCC）、SCCに入るIN、SCCから出るOUT、INとOUTを結ぶTUBE、INとOUTから伸びるひげ（TENDRIL）から構成されるネットワークである。

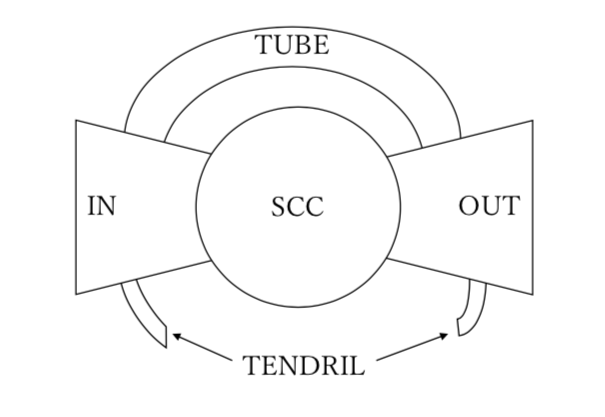
上の画像のような構造をしていて、その見た目からBow-tie構造と呼ばれている。

隣接行列（adjacency）と行列積

このネットワークの隣接行列$A$は

A = 
\begin{pmatrix}
0 & 1 & 0 \\
0 & 0 & 1 \\
0 & 0 & 0
\end{pmatrix}

また、２の頂点の位置ベクトル$x$は

x = 
\begin{pmatrix}
0 \\
1 \\
0
\end{pmatrix}

隣接行列$A$と位置ベクトル$x$の行列積$Ax$,$xA$はそれぞれ

x^TA = 
\begin{pmatrix}
0\\
0\\
1
\end{pmatrix}^T
Ax = 
\begin{pmatrix}
1\\
0\\
0
\end{pmatrix}

このようにある位置ベクトルに隣接行列を右からかけると矢印方向にすすみ、左からかけると矢印方向と逆に辿る形となる。

ここでネットワークに自己ループを持たせ、この行列積を用いるとIN、OUT、TENDRILが一つのベクトルで表すことができるだろう。

Bow-tie構造の分類

Bow-tie構造を分類する。
はじめにimportするライブラリは

import numpy as np
import networkx as nx
import scipy

次に分類するコードは以下である。

bow_tie.py

def bow_tie(G):
    np.seterr(divide='ignore', invalid='ignore')#0徐算で起こるWarningを表示しない
    components = max(nx.strongly_connected_components(G), key=len)
    components  = list(components)
    nodes = list(G.nodes())
    length = G.number_of_nodes()
    adjacency = nx.to_scipy_sparse_matrix(G)
    adjacency = adjacency + scipy.sparse.eye(length)#自己ループ付きのadjacency
    scc = np.zeros(length)
    ones = np.ones(length)
    intersects = np.isin(nodes, components)#重複する要素True
    indices = np.where(intersects)#重複するnodesのindex
    scc[indices] = 1
    scc_difference = ones - scc
    scc_copy = scc
    loop1 = [1]
    for i in loop1:
        scc_in1 = adjacency @ scc_copy#行列積
        scc_in2 = adjacency @ scc_in1
        if np.count_nonzero(scc_in2) != np.count_nonzero(scc_in1):#全てのINを網羅すると0の数が一致する。
            loop1.append(i+1)
            scc_copy = scc_in1
        else:
            scc_in1 = scc_in1 * scc_difference#要素積を用い、SCCを省く
            scc_in1 /= scc_in1#０徐算が起こる
            scc_in1 = np.nan_to_num(scc_in1)#NaN to 0
    scc_copy = scc
    loop2 = [1]
    for i in loop2:
        scc_out1 = scc_copy @ adjacency
        scc_out2 = scc_out1 @ adjacency 
        if np.count_nonzero(scc_out2) != np.count_nonzero(scc_out1):
            loop2.append(i+1)
            scc_copy = scc_out1
        else:
            scc_out1 = scc_out1 * scc_difference
            scc_out1 /= scc_out1
            scc_out1 = np.nan_to_num(scc_out1)
    difference = scc_difference - scc_in1 - scc_out1
    in_copy = scc_in1
    loop3 = [1]
    for i in loop3:
        in_tendril1 = in_copy @ adjacency
        in_tendril1 = in_tendril1 * difference
        in_tendril2 = in_tendril1 @ adjacency
        in_tendril2 = in_tendril2 * difference
        if np.count_nonzero(in_tendril2) != np.count_nonzero(in_tendril1):
            loop3.append(i+1)
            in_copy = in_tendril1
        else:
            in_tendril1 /= in_tendril1
            in_tendril1 = np.nan_to_num(in_tendril1)
    out_copy = scc_out1
    loop4 = [1]
    for i in loop4:
        out_tendril1 = (adjacency @ out_copy) * difference
        out_tendril2 = (adjacency @ out_tendril1) * difference
        if np.count_nonzero(out_tendril2) != np.count_nonzero(out_tendril1):
            loop4.append(i+1)
            out_copy = out_tendril1
        else:
            out_tendril1 /= out_tendril1
            out_tendril1 = np.nan_to_num(out_tendril1)
    in_sum = np.sum(scc_in1)
    out_sum = np.sum(scc_out1)
    if in_sum == 0 and out_sum == 0:#INとOUTがなかった場合
        tube = np.zeros(length)
    elif in_sum == 0 or out_sum ==0:
        tube = np.zeros(length)
    else:
        tube = in_tendril1 * out_tendril1
        in_tendril1 = in_tendril1 - tube
        out_tendril1 = out_tendril1 - tube
    return scc, scc_in1, scc_out1, in_tendril1, out_tendril1, tube#, [loop1[-1], loop2[-1], loop3[-1], loop4[-1]]

実際に動かす

実際に分類できるかどうか動かしてみる。
以下の画像を分類する。

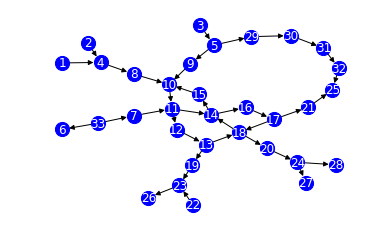
bow_tie(G)
#(array([0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1,
#        1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0]),
# array([1., 1., 1., 1., 0., 1., 0., 1., 0., 1., 1., 1., 0., 0., 0., 0., 0.,
#        0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]),
# array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1.,
#        0., 0., 0., 0., 0., 0., 0., 1., 1., 0., 1., 1., 1., 1., 1., 1.]),
# array([0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
#        0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]),
# array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
#        0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0.]),
# array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 1., 1., 1., 0.,
#        0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]))

このように分類できた。
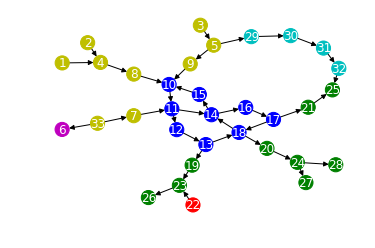
それではこれをもとに頂点を色分けする。

color = []
a = bow_tie(G)
for i in range(len(a[0])):
    if a[0][i] == 1:#SCC
        color.append('b')#青
    elif a[1][i] == 1:#IN
        color.append('y')#黄色
    elif a[2][i] == 1:#OUT
        color.append('g')#緑
    elif a[3][i] == 1:#IN_TENDRIL
        color.append('m')#マゼンタ
    elif a[4][i] == 1:#OUT_TENDRIL
        color.append('r')#赤
    elif a[5][i] == 1:#TUBE
        color.append('c')#シアン
    else:
        color.append('k')#黒

描画ライブラリであるmatplotlibをimportし、

import matplotlib.pyplot as plt

以下のコードを実行する。

pos = nx.nx_pydot.pydot_layout(G)
nx.draw_networkx(G, pos=pos, node_size=200, node_color=color, font_color='w')
plt.axis('off')
plt.gca().invert_yaxis()
plt.show()

出力結果

うまく分類できている。

最後に

まあまあな速さでうまく分類できていると思う
とても大きなノードを持つネットワークで分類できないノードがあった。
どこかに不備や修正箇所があると思うがお手上げ状態である。
ひげのひげまでは分類していないが、それを分類しようとするとキリがないのでここまでにしておく。

間違っている部分や修正箇所のご指摘をお願いします。