ネットワーク(グラフ)
グラフ理論で呼ばれるネットワーク(グラフ)とは,会社の取引関係や論文の共著関係,俳優の共演関係に見られるような,ノード(会社,著者,俳優)の集合$V$とリンク(取引関係,共著関係,共演)の集合$E$のペアであり,$G=(V, E)$と表す.またここでは単純グラフ(自己ループや多重辺が存在しないグラフ)を扱う.
例として,A社とB社が取引関係があり,またB社とC社に取引関係があるというネットワーク$G$を図示する.
ネットワーク生成の関数はpythonのnetworkxを用いる.
import networkx as nx
G = nx.Graph()
G.add_edge('A', 'B')
G.add_edge('B', 'C')
nx.draw_networkx(G)
隣接行列
隣接行列は,グラフのリンクがどのノードとつながっているかを行列形式で表したものである.
A = \Bigr(\,A_{ij}\,\Bigr) =\left\{
\begin{array}{ll}
1 & (if\,node\,j\,and\,i\,is\,connected) \\
0 & (otherwise)
\end{array}
\right.
例の隣接行列は以下である.
adjacency = nx.to_numpy_array(G)
print(adjacency)
# array([[0., 1., 0.],
# [1., 0., 1.],
# [0., 1., 0.]])
ネットワークが無向であるとき,隣接行列は対称行列となる.
A_{ij} = A_{ji} \;(if \,G\,is\,undirected)
次数
次数$k_i$とは,ノード$i$がつながっているリンクの総数である.
つまり隣接行列の列(または行)の和である.
k_i = \sum_{l=1}A_{il}
例の各次数は以下である.
import numpy as np
degree = np.sum(adjacency, axis=1)
print(degree)
# array([1., 2., 1.])
各次数の値が対角成分になる行列$D$を,次数行列という。
D = \Bigr(\,D_{ij}\,\Bigr) =\left\{
\begin{array}{ll}
k_i &
(i = j) \\
0 & (i ≠ j)
\end{array}
\right.
また,握手補題により以下が成り立つ.
\sum_{i=1}k_i = 2|E|
print(np.sum(degree))
# 4.0
平均次数とはあるノードから伸びるリンクの平均値である.つまりネットワークのノード数を$n$とすると
<k> = \frac{\sum_{i=1}k_i}{n} = \frac{2|E|}{n}
Laplacian行列
ラプラシアン行列$L$とは次数行列と隣接行列の差の行列である.
L = D - A
次数行列$D$は対角成分以外$0$なので,$L$も$G$が無向ネットワークのとき対称行列となる.
例のラプラシアン行列は,
laplacian = nx.laplacian_matrix(G)
print(laplacian)#Sparse Matrix
# (0, 0) 1
# (0, 1) -1
# (1, 0) -1
# (1, 1) 2
# (1, 2) -1
# (2, 1) -1
# (2, 2) 1
Laplacian行列の逆行列
Laplacian行列は正則行列ではない.Laplacian行列の列(または行)の和を取ると全て0になるため.
よって特異値分解を用いて,擬似逆行列を作る.
Laplacian行列は,対称行列であるため,固有値分解を用いる.
L = P\, \Lambda \,P^T
ここで$P=\bigr(,P_i,\bigr)$は固有値$\lambda _i$に対応する
正規直交化を行った固有ベクトル$P _i$の行列である.
よって$L$の逆行列を考える際は固有値を考えれば良い.
Laplacian行列の固有値
例の固有値を求める.
laplacian = laplacian.toarray() # sparse to array
eig = np.linalg.eigh(laplacian)
print(eig)
# array([9.99658224e-17, 1.00000000e+00, 3.00000000e+00])
ここで複雑ネットワーク(ノード数,リンク数が大きなネットワーク)でのLaplacian行列を考える.
ここで用いるモデルはErdős–Rényi model(リンクを確率的に生成するモデル)である.
ノード数5000,平均次数を10となるよう調整する.
n = 5000
p = 10 / n
Ger = nx.fast_gnp_random_graph(n, p)
laplacian = nx.laplacian_matrix(Ger)
laplacian = laplacian.toarray()
eig = np.linalg.eigh(laplacian)
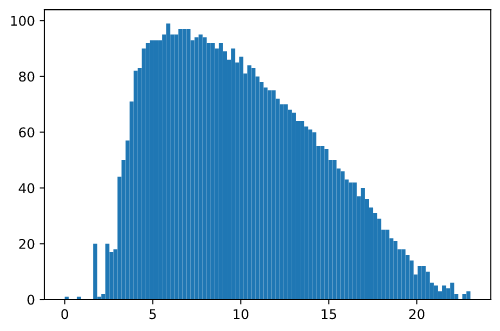
得られた固有値をヒストグラムで表す.
import matplotlib.pyplot as plt
plt.hist(eig[0], bins=100)
plt.show()
このように,固有値0が一つ存在していることがわかる.また0固有値以外の固有値は全て正の値を取り,固有値の分布にも規則性が読み取れる.
よってこのモデルにおいてラプラシアン行列の逆行列も同様に規則性が読み取れるはずである.
参考文献
『Network Science by Albert-László Barabási』(http://networksciencebook.com)
『Laplacian Matrix』(https://www.sciencedirect.com/topics/computer-science/laplacian-matrix )
ハワード・アントン(1979)『アントンのやさしい線型代数』山下純一訳,現代数学社