Go to Qiita Advent Calendar 2024 Top
LoginSignup
4
9

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@honocat

ベイズ統計でKaggleを解いてみる

Last updated at Posted at 2024-04-10

はじめに

概要

ベイズ統計を用いてKaggleの1タイタニック問題を解いてみる．

分析は以下の手順で行う．

  1. データの可視化・理解
  2. データの加工・前処理
  3. ベイズ統計分析
    1. モデルの記述
    2. デザイン行列・データリストの作成
    3. Stanファイルの記述
    4. MCMC!
  4. 結果の評価

実行環境

  • Mac OS Sonoma 14.1
  • R version 4.3.1
  • RStudio version 2023.12.1+402
$ sw_vers
ProductName:		macOS
ProductVersion:		14.1
BuildVersion:		23B74

> R.versions
version.string R version 4.3.1 (2023-06-16)
> sessionInfo()
other attached packages:
 [1] posterior_1.5.0 cmdstanr_0.6.1  lubridate_1.9.3 forcats_1.0.0  
 [5] stringr_1.5.0   dplyr_1.1.3     purrr_1.0.2     readr_2.1.4    
 [9] tidyr_1.3.0     tibble_3.2.1    ggplot2_3.4.4   tidyverse_2.0.0

準備

以下のコードを実行しておく．

# titanic.R

> pacman::p_load(tidyverse,
                 cmdstanr,
                 posterior)
> options(mc.cores = parallel::detectCores())

1. データの可視化・理解

まず，Kaggleのタイタニック問題のページから分析に用いるtrain.csv, test.csvをダウンロードし，読み込む．

# titanic.R

> data_train <- read.csv('train.csv')
> data_test <- read.csv('test.csv')

2つに分かれているのは面倒なので結合して1つのデータフレームとする．

# titanic.R

> data_test$Survived <- NA # test.csvには'Survived'がないので追加
> df <- rbind(data_train, data_test)

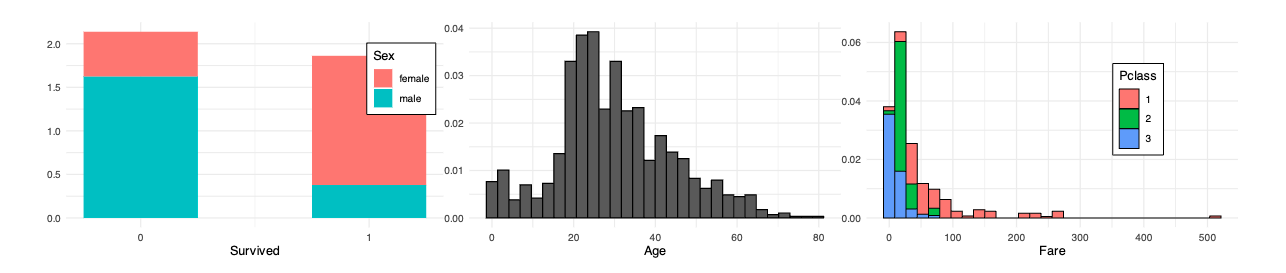
確認すると，Age, Fare, Cabin, Embarkedの4つの変数に欠損がある2．欠損値の処理方法にはいくつかあるが，今回は代入法を使う．

以下はSurvived, Age, Fareそれぞれの分布を可視化したものである．

data_plot.png

2.データの加工・前処理

次にデータの加工・前処理を行う．前章で確認したAge, Fareの欠損値を処理する．Cabin, Embarkedは分析に用いないので省略．

Fareの欠損処理

Fareの欠損は1つだけであるから，単一代入法を用いて欠損を補う．前章で確認したFareの分布より，この変数は客室のクラスであるPclassに依存していることがわかるため，この情報を用いて代入する値を決める．

# titanic.R

> df |> filter(is.na(Fare) == TRUE)
  PassengerId Survived Pclass               Name  Sex  Age SibSp Parch Ticket Fare Cabin Embarked
1        1044       NA      3 Storey, Mr. Thomas male 60.5     0     0   3701   NA  <NA>        S

欠損データを確認すると，Pclass = 3であるから，Pclass = 3のデータのみで計算した平均値を代入する．

# titanic.R

> df_pclass3 <- df |> filter(Pclass == 3)
> mean_fare_pclass3 <- df_pclass3$Fare |>
    mean(na.rm = TRUE)
> df <- df |>
    mutate(Fare = ifelse(is.na(Fare) == TRUE, mean_fare_pclass3, Fare))

Ageの欠損処理

Ageの欠損処理にはベイズ統計を用いる( 適しているかはわからない )．

Ageが欠損していないデータを用いて，Ageを結果変数，Pclass, Sex, SibSp, Parch, Fareを説明変数としてベイズ統計分析を行い，その結果を用いてAgeが欠損しているデータの値を予測するというものである．

ここでRのパッケージである{cmdstanr}を用いる．このパッケージを用いたベイズ統計分析を行う際の手順は以下の通りである．

  1. 統計モデルを記述する
  2. デザイン行列・データリストを作成する
  3. Stanファイルを記述する
  4. MCMCを実行する
  5. 結果を評価する

1. 統計モデルを記述する

まず，分析に用いる統計モデルを記述する．

\begin{align}
    y_i & \sim \text{Normal} (\mu_i, \sigma)　& (尤度関数) \\
    \mu_i & = \beta_1 + \beta_2 x_{pcl, i} + \beta_3 x_{sex, i} +
        \beta_4 x_{sib, i} + \beta_5 x_{par, i} + \beta_6 x_{far, i}
        & (リンク関数) \\
    \beta_k & \sim \text{Normal} (0, 10) \quad (k = 1, 2, ..., 6) & (事前分布)
\end{align}

前章で確認したAgeの分布より，尤度関数には正規分布を用いる．また，事前分布は$\mu = 0, \sigma = 10$の正規分布を採用する．

2. デザイン行列・データリストを作成する

次に，Rに戻ってStanファイルに引き渡すデザイン行列とデータリストを作成する．

# titanic.R

# Ageが欠損していないデータのみ抽出
> df_fillNA <- df |>
    filter(is.na(Age) == FALSE)

今回使うデザイン行列は2つあり，分析に用いる(Ageが欠損していない)ものと予測に用いる(Ageが欠損している)ものである．前者は以下のコードで作成できる．

# titanic.R

> formula_fillNA <- formula(Age ~ Pclass + Sex + Parch + Fare)
> design_fillNA <- model.matrix(formula_fillNA, df)
> head(design_fillNA)
  (Intercept) Pclass Sexmale SibSp Parch    Fare
1           1      3       1     1     0  7.2500
2           1      1       0     1     0 71.2833
3           1      3       0     0     0  7.9250
4           1      1       0     1     0 53.1000
5           1      3       1     0     0  8.0500
6           1      1       1     0     0 51.8625

後者は少し工夫して作成する．

# titanic.R

> design_fillNA_pred <- df |>
    filter(is.na(Age) == TRUE) |>                      # Ageが欠損しているデータ
    mutate(Intercept = rep(1, times = n())             # 切片の追加
           Sex       = ifelse(Sex == 'male', 1, 0) |>  # Sexの書き換え
    select(Intercept, Pclass, Sex, SibSp, Parch, Fare) # 説明変数のみ抽出
> head(design_fillNA_pred)
  Intercept Pclass Sex SibSp Parch    Fare
1         1      3   1     0     0  8.4583
2         1      2   1     0     0 13.0000
3         1      3   0     0     0  7.2250
4         1      3   1     0     0  7.2250
5         1      3   0     0     0  7.8792
6         1      3   1     0     0  7.8958

次に，Stanファイルに引き渡すデータリストを作成する．

# titanic.R

> data_fillNA <- list(
    N = nrow(df_fillNA),               # サンプルサイズ(分析)
    K = ncol(design_fillNA),           # デザイン行列の列数
    Y = df_fillNA$Age,                 # 結果変数の値
    X = design_fillNA,                 # デザイン行列(分析)
    N_pred = nrow(design_fillNA_pred), # サンプルサイズ(予測)
    X_pred = design_fillNA_pred        # デザイン行列(予測)
  )

3. Stanファイルを記述する

1.で記述した統計モデル，2.で作成したデザイン行列・データリストを取り入れたStanファイルを記述する．

// fillNA.stan

data {
    int<lower=0> N;      // サンプルサイズ
    int<lower=0> K;      // デザイン行列の列数
    vector[N] Y;         // 結果変数の値
    matrix[N, K] X;      // デザイン行列
    int<lower=0> N_pred; // サンプルサイズ(予測)
    matrix[N, K] X_pred; // デザイン行列(予測)
}

parameters {
    vector[K] beta;      // リンク関数のパラメタ(係数ベクトル)
    real<lower=0> sigma; // 尤度関数のパラメタ(正規分布の標準偏差)
}

model {
    Y ~ normal(X * beta, sigma); // 尤度関数
}

generated quantities {
    vector[N_pred] Y_pred; // 予測値
    for (i in 1:N_pred) {
        Y_pred[i] = normal_rng(X_pred[i,] * beta, sigma);
    }
}

4. MCMCを実行する

Rに戻って，先ほど作成したStanファイルをコンパイルし，MCMCを実行する．

# titanic.R

# コンパイル
> stan_fillNA <- cmdstan_model('fillNA.stan')
# MCMC!
> fit_fillNA <- stan_fillNA$sample(
    data = data_fillNA,
    seed = 123,
    chains = 4,
    refresh = 1000,
    iter_warmup = 1000,
    iter_sampling = 3000
  )
Running MCMC with 4 chains, at most 8 in parallel...

All 4 chains finished successfully.
Mean chain execution time: 1.5 seconds.
Total execution time: 1.7 seconds.

5. 結果の評価

結果を確認する(収束の確認は問題なさそうなので省略)．

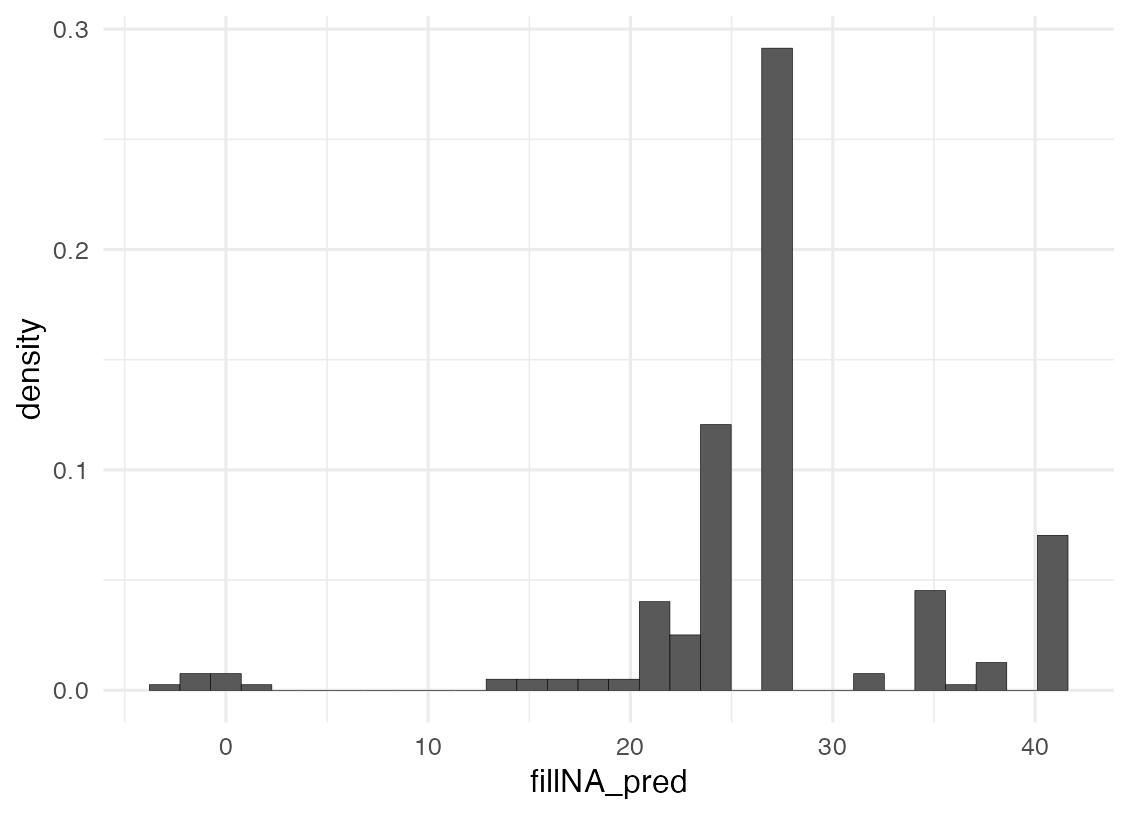
ベイズの結果は各データ(各乗客)のAgeを12,000回予測している．その平均をAgeの値として採用する．

# titanic.R

> post_fillNA <- fit_fillNA$draws() |>   # 結果をデータフレームに変換
    as_draws_df()
> fillNA <- post_fillNA |>               # 各データの予測値の平均を抽出
    select(`Y_pred[1]`:`Y_pred[263]`) |>
    apply(2, mean) |>
    round(2)

fillNA.png

年齢の予測値がマイナスになっているデータがあるので，元のデータの最小値で置き換える．

# titanic.R

> fillNA_pred <- ifelse(fillNA_pred <= 0, min(df$Age, na.rm = TRUE), fillNA_pred)

これを元のデータdfに反映する．

# titanic.R

> n <- 1                             # 便宜上用いるインデックス
> for (i in 1:nrow(df)) {
    if (is.na(df[i,]$Age) == TRUE) { # Ageが欠損しているデータの時{}内が実行される
        df[i,]$Age <- fillNA_pred[n]
        n <- n + 1
    }
  }

これで欠損値の処理が完了した．

3. ベイズ統計分析

先ほどと同じ手順でメインのベイズ統計分析を行う．

1. モデルの記述

今回は生存したか否かの予測であるから，結果変数Survivedはベルヌーイ分布に従うとする．またリンク関数にはロジット関数を，事前分布には正規分布を仮定する．

\begin{align}
    y_i & \sim \text{Bernolli} (\theta_i) & (尤度関数) \\
    \text{logit} (\theta_i) & = \beta_1 + \beta_2 x_{pcl, i} +
        \beta_3 x_{sex, i} + \beta_4 x_{age, i} + \\
        & \beta_5 x_{sib, i} + \beta_6 x_{par, i} + \beta_7 x_{far, i} & (リンク関数) \\
    \beta_k & \sim \text{Normal} (0, 10) \quad (k = 1, 2, ..., 7) & (事前分布)
\end{align}

2. デザイン行列・データリストの作成

例によって，分析に用いるデザイン行列(train.csvにあたる)と，予測に用いるデザイン行列(test.csvにあたる)の2つを作成する．

その前に，まずdfをSurvivedが欠損していないdf_trainと，Survivedが欠損しているdf_testに分ける．

# titanic.R

> df_train <- df |>
    filter(is.na(Survived) == FALSE)
> df_test <- df |>
    filter(is.na(Survived) == TRUE)

この2つのデータフレームを用いてデザイン行列を作成する．

# titanic.R

# train
> formula_train <- formula(Survived ~ Pclass + Age + SibSp + Parch + Fare)
> design_train <- model.matrix(formula_train, df_train)
# test
> design_test <- df_test |>
    mutate(Intercept = rep(1, times = n()),
           Sex       = ifelse(Sex == 'male', 1, 0)) |>
    select(Intercept, Pclass, Sex, Age, SibSp, Parch, Fare)

次にデータリストを作成する．

# titanic.R

> data_titanic <- list(
    N = nrow(df_train),     # サンプルサイズ(分析)
    K = ncol(design_train), # デザイン行列の列数
    Y = df_train$Survived,  # 結果変数の値
    X = design_train,       # デザイン行列(分析)
    N_pred = nrow(df_test), # サンプルサイズ(予測)
    X_pred = design_test    # デザイン行列(予測)
  )

3. Stanファイルを記述する

分析に用いるStanファイルは以下である．

// titanic.stan

data {
    int<lower=0> N;           // サンプルサイズ(分析)
    int<lower=0> K;           // デザイン行列の列数
    array[N] int Y;           // 結果変数の値
    matrix[N, K] X;           // デザイン行列(分析)
    int<lower=0> N_pred;      // サンプルサイズ(予測)
    matrix[N_pred, K] X_pred; // デザイン行列(予測)
}

parameters {
    vector[K] beta;
}

model {
    Y ~ bernolli(inv_logit(X * beta));
}

generated quantities {
    vector[N_pred] Y_pred;
    for (i in 1:N_pred) {
        Y_pred[i] = bernolli_rng(inv_logit(X_pred[i,] * beta));
    }
}

4. MCMCを実行する

Rで，Stanファイルをコンパイルし，MCMCを実行する．

# titanic.R

# コンパイル
> stan_titanic <- cmdstan_model('titanic.stan')
# MCMC!
> fit_titanic <- stan_titanic$sample(
    data = data_titanic,
    seed = 1912-04-14,
    chains = 4,
    refresh = 1000,
    iter_warmup = 1000,
    iter_sampling = 3000
  )
Running MCMC with 4 chains, at most 8 in parallel...

All 4 chains finished successfully.
Mean chain execution time: 3.3 seconds.
Total execution time: 3.6 seconds.

5. 結果を評価する

rhat, トレースプロットを確認すると，問題なく収束していそうである．

今回も，ベイズの結果は，各データ(各乗客)に対して12,000回生死を予測している．生存の確率が50%以上ならSurvived = 1(生存)，50%未満ならSurvived = 0(死亡)と判断する．

# titanic.R

> post_titanic <- fit_titanic$draws() |> # 結果をデータフレームに変換
    as_draws_df()
> res <- post_titanic |>                 # 各乗客の生存確率を`res`に格納
    select(`Y_pred[1]`:`Y_pred[418]`) |>
    apply(2, mean)
> Survived_pred <- rep(NA, times = nrow(df_test)) # 予測値を格納する空のベクトル
> for (i in 1:nrow(df_test)) {
    Survived_pred[i] <- ifelse(res[i] < 0.5, 0, 1)
  }

5. 結果の評価

得られた予測値を元のデータフレームに代入して，結果を確認する．

# titanic.R

> df_test <- df_test |>
    mutate(Survived = Survived_pred)

result.png

# titanic.R

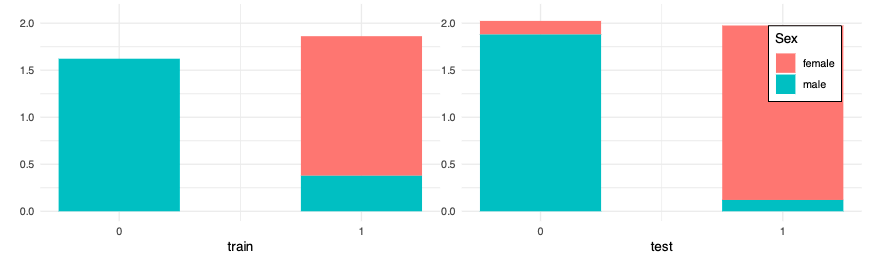
> table(df_train$Sex) / nrow(df_train) * 100
 female    male 
35.2413 64.7587 
> table(df_test$Sex) / nrow(df_test) * 100
  female     male 
36.36364 63.63636

df_train, df_testの男女比はほぼ一緒である．それを考慮すると，予測にやや偏りがあるように見える(女性のほうが生き残ると予測されがちである)．

データの提出

分析の結果を.csvファイルに書き出して提出をする．

# titanic.R

> df_test |>
    select(PassengerId, Survived) |>
    write_csv('titanic_nh.csv')

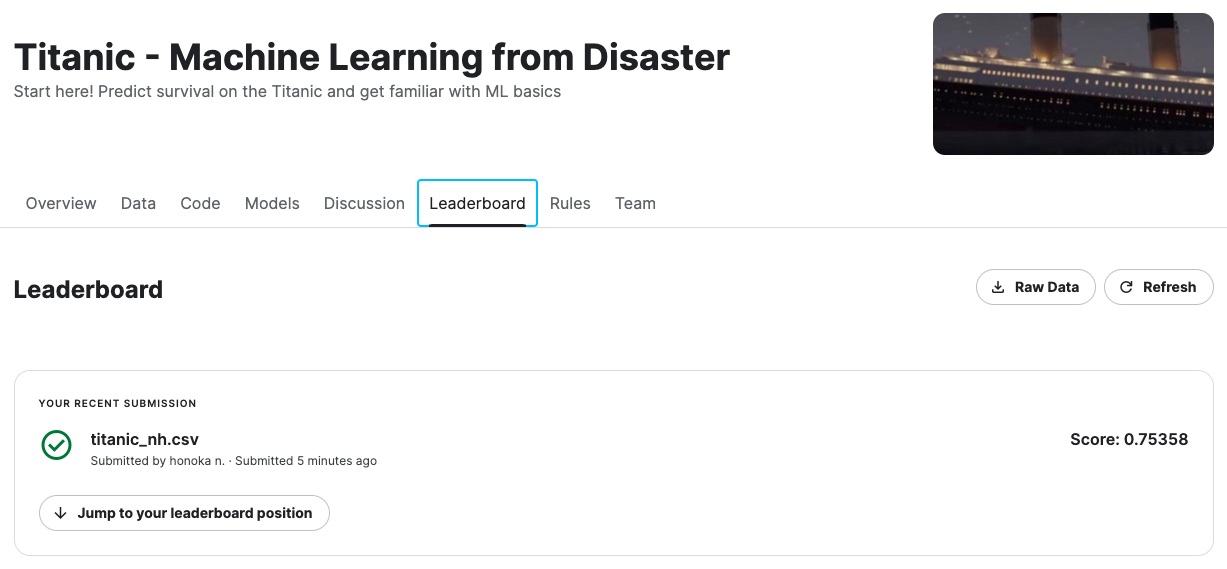
Kaggleのタイタニック問題のページへアクセスして，右上のSubmit Predictionのボタンで提出できる．

ちなみに今回の結果は，正答率約75%だった．

kaggle.png

改善できるところ

  • 欠損値の処理方法
  • モデルに含める変数の取捨選択

  1. 1912年4月14日に沈没したタイタニック号の乗客データを用いて，各乗客が生存したか死亡したかを予測するものである． ↩

  2. Age, Fareには欠損値としてNAが入っている．しかしCabin, Embarkedに関しては欠損部分にNAが入っているのではなく空白("")となっているため，別途処理が必要． ↩

4
9
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
4
9

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?